---

迭代實現快速冪

實現 pow(x, n) ，即計算 x 的 n 次冪函數（即，xn）。不得使用庫函數，同時不需要考慮大數問題。

示例 1：

輸入：x = 2.00000, n = 10
輸出：1024.00000

示例 2：

輸入：x = 2.10000, n = 3
輸出：9.26100

示例 3：

輸入：x = 2.00000, n = -2
輸出：0.25000
解釋：2^-2 = 1/2² = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= xn <= 104

---

思路

想用累乘處理冪路子就走窄了，超時是板上釘釘的。

用快速冪的思想才符合題目考察的意圖，在詳說快速冪之前說一個很刁鉆的測試用例 —— n=-2147483648。

int的取值范圍

我們知道：

• int的取值范圍是-2147483648（-2³¹）到2147483647（2³¹ - 1）
• -2147483648有一位符號位可用，因此2147483647是32位操作系統中最大的符號型整型常量。
• 當出現這個刁鉆的測試用例時，如果對n粗暴的取絕對值的話，int是容納不下的，因此當 n<0 時， 需要定義一個long long類型變量 m 來存儲 n 的絕對值。

快速冪

從二進制的角度來理解

• 對于任何十進制正整數 n ，設其二進制為
  則有：

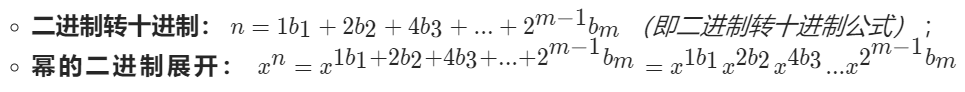
• 根據以上推導，可把計算 xⁿ 轉化為解決以下兩個問題：

• 因此，應用以上操作，可在循環中依次計算
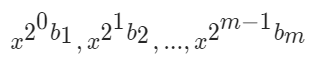
  的值，并將所有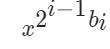累計相乘即可。

---

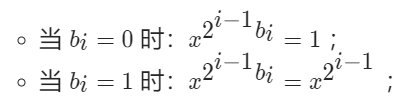
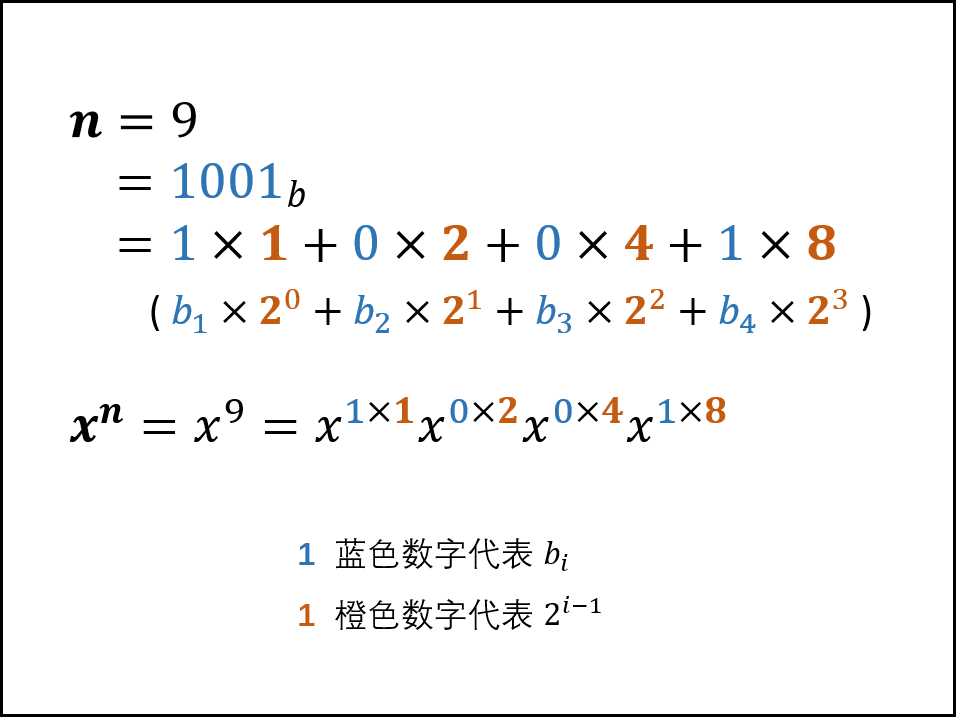
從二分法的角度來理解

快速冪實際上是二分思想的一種應用。

• 二分推導： xⁿ = x^n/2 × x^n/2 = （x²)^n/2，令 n/2 為整數，則需要分為奇偶兩種情況（設向下取整除法符號為 “//” ）：

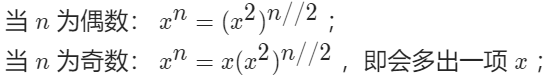
• 冪獲取結果：

1. 根據二分推導，可通過循環 x = x² 操作，每次把冪從 n 降至 n//2 ，直至將冪降為 0 ；
2. 設 sum=1 ，則初始狀態 xⁿ = xⁿ × sum。在循環二分時，每當 n 為奇數時，將多出的一項 x 乘入 sum ，則最終可化至 xⁿ = x⁰ * sum = sum，返回 sum 即可。

轉自作者：jyd

算法流程：

1. 當 x = 0 時：直接返回 0 （避免后續 x = 1 / x 操作報錯）。
2. 初始化 sum = 1 ；
3. 當 n < 0 時：把問題轉化至 n≥0 的范圍內，即執行 x = 1/x ，n = - n ；
4. 循環計算：當 n = 0 時跳出；

• 當 n&1=1 時：將當前 x 乘入 sum（即 sum?=x ）；
• 執行 x = x²（即 x?=x ）；
• 執行 n 右移一位（即 n>>=1）。

5. 返回 sum。

代碼

class Solution {
public:double myPow(double x, int n) {if(x == 0) return 0;double sum = 1;long long m = n;if(n < 0){x = 1.0/x;m = -m;}while(m > 0){if(m & 1){sum *= x;}x *= x;m >>= 1;}return sum;}
};

復雜度分析

• 時間復雜度 O(log_2 n)： 二分的時間復雜度為對數級別。
• 空間復雜度 O(1)： sum， b 等變量占用常數大小額外空間。

---

進階——超級次方

計算 a^b 對 1337 取模，a 是一個正整數，b 是一個非常大的正整數且會以數組形式給出。

---

思路

本題的難點在于對 數組b 的處理，顯然無法將其轉為 一個具體類型，因此解決方法無非就是 在 倒序 or 正序 遍歷數組的同時進行次方處理。

倒序+快速冪

本質無非就是把上面提到的二進制思想轉為十進制，具體來說：

2²³ 可以看作 2⁽¹⁰ * ^{2) + (1} * ³⁾ ，也就是 1024² * 2³ 。

那么我們只需要在第 k 次 倒序遍歷 數組 b 的同時，記錄 a 的 10^k-1 次方即可。

---

正序+快速冪

思路源于秦九韶算法，一般地，一元 n 次多項式的求值需要經過 $\frac{(n+1)?n}{2}$ 次乘法和 $n$ 次加法，而秦九韶算法只需要 $n$ 次乘法和 $n$ 次加法。大大簡化了運算過程。

把一個 n 次多項式：

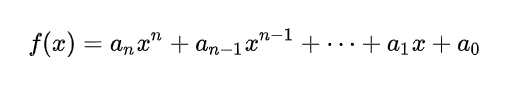
改寫成如下形式：

舉個具體的例子，計算 $2^{234}$：

$2^{234}=2^{200+30+4}=2^{200}?2^{30}?2^4=(2^{20}?2^3{)}^{10}?2^4=[(1^{10}?2^2{)}^{10}?2^3{]}^{10}?2^4$

最后一步推導實際上是對規律的歸納，即：以 1 作為初始值 res，每次有 新項 加入時，對 res 執行 $res=re{s}^{10}?新項$ 的操作。

---

代碼

class Solution {const int MOD = 1337;int quickmul(int x, int n){ // 快速冪實現pow功能if(x == 0) return 0;int sum = 1;while(n){if(n&1) sum = (long)sum * x % MOD;n >>= 1;x = (long)x * x % MOD;}return sum;}
public:int superPow(int a, vector<int>& b) { // 倒序int res = 1, n = b.size();for(int i=n-1; i>=0; i--){res = (long)res * quickmul(a, b[i]) % MOD;a = quickmul(a, 10); // 記錄當前 a 的冪}return res;}int superPow(int a, vector<int>& b) { // 正序int res = 1, n = b.size();for(int i : b){res = (long)quickmul(res, 10) * quickmul(a, i) % MOD;// 加入新項時，對 res 執行 res = res^10 * 新項 的操作}return res;}
};

---

復雜度分析

• 時間復雜度O(${\sum }_{i=0}^{n?1}\log b_i$)： 其中 n 是數組 b 的長度，對每個 $b_i$ 計算快速冪的時間為 O($\log b_i$)。
• 空間復雜度O(1)： 過程由迭代實現，避免了遞歸方法對棧空間的占用，只需要常數的空間存放若干變量。