---

題目

輸入數字 n，按順序打印出從 1 到最大的 n 位十進制數。比如輸入 3，則打印出 1、2、3 一直到最大的 3 位數 999。

示例 1:

輸入: n = 1
輸出: [1,2,3,4,5,6,7,8,9]

說明：

用返回一個整數列表來代替打印
n 為正整數

來源：力扣（LeetCode）

---

思路

在力扣里這道題不用考慮大數。但是還是想自己寫一個以備不虞。

重點：

1. 用 string 處理大數。
2. 處理每一位時，將 int 轉換為 char。
3. 用 遞歸+分治 的思想生成 位數n 對應的 全排列。
4. 將生成的全排列依次壓入 vector<int> 中，按題目要求返回整數列表。

細節：

• 第一點無需贅述。

• 關于第二點：

我們知道 string 每一位下標對應的元素其類型都是 char 的（字符串由字符組成嘛）。

那代碼實現應該怎么寫呢？是這樣嗎？

s[digit] = (char)i;

答案是否定的。來看這么一段代碼：

可以看到輸出結果不是4，而是52。

簡單的 (char)i 起到的作用是將 i 變為 ASCII碼為i的字符，上圖中，因為字符’4’ 的ASCII碼為52，因此 char(52) 會得到 字符'4'。

換言之，s[digit] = (char)i; 得到的是 ASCII碼為i時對應的字符 ，而非 字符'i'。

正確處理 int 轉 char 應為（例如：將整數4轉換為字符4）：

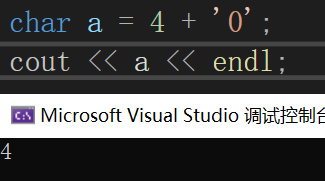
上圖代碼的本質也就是 0的ASCII碼(48)+4 得到 ASCII碼52，其對應的字符便是 '4'。

值得一提的是，通過 + '0' 將 int 轉換為 char 并非總是可行的。當整數大于9時， + '0' 操作得到的便不再是數字字符了：

當然對于本題來講并不存在這樣的問題，因為我們僅僅是轉換每個數位上的數字（它們在0~9之間）。

• 關于第三點，也是本題最重要的部分：

全排列思想如下圖所示（圖源大佬：jyd）：

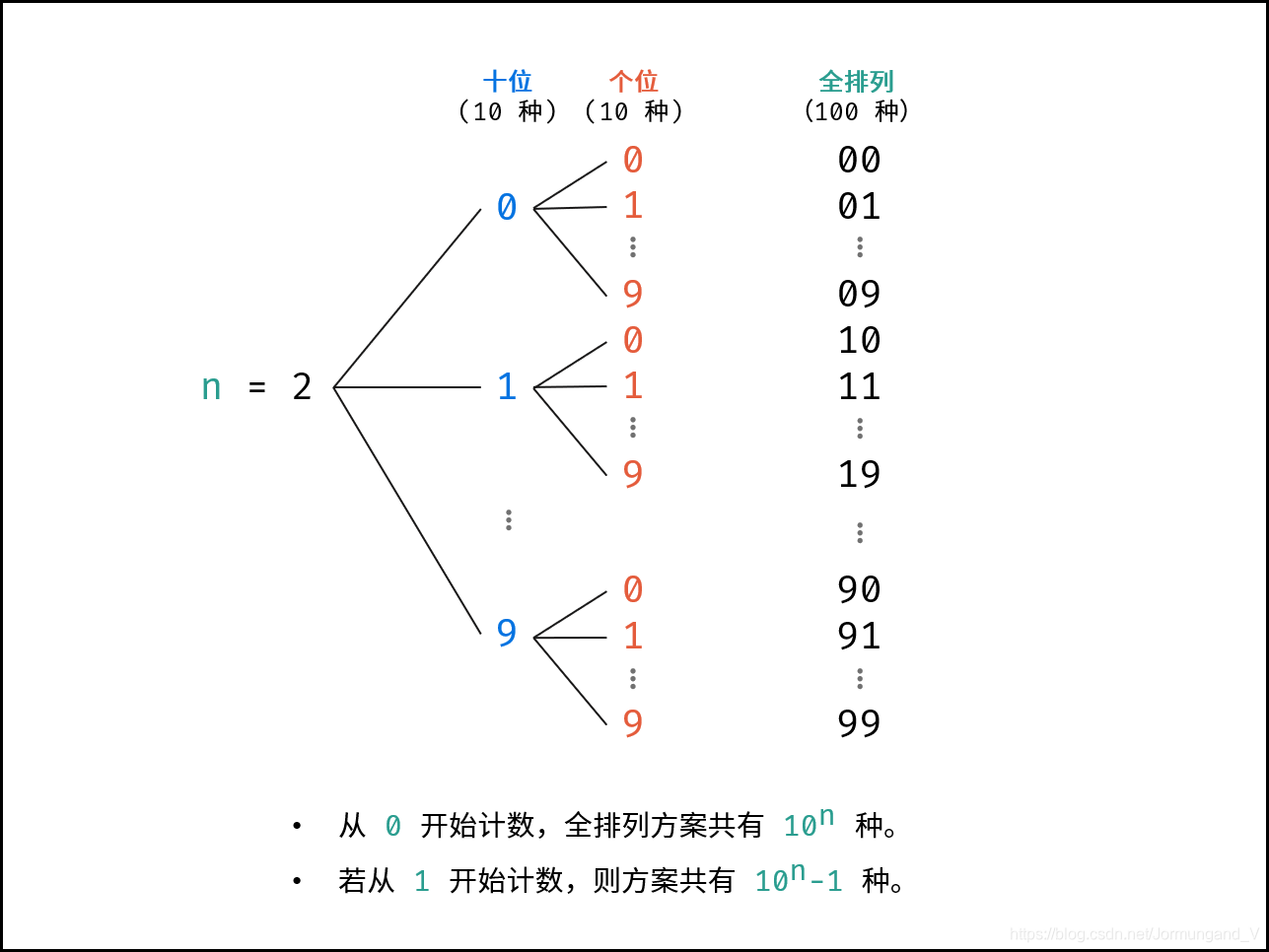
代碼中用 dfs函數 實現：

1. 用分治思想先固定高位(digit=0) string[digit]（圖中藍色部分）
2. 再依次固定低位（digit+1），將 digit+1 作為新參數傳入 函數dfs（圖中紅色部分）
3. 當 digit == n 時，此時已將每一位都處理完了，將string轉換為int，并判斷int是否為0，不為0則加入用來保存結果的 vector<int> 。（將string轉換為int之后的操作僅僅是針對本題要求的返回證書列表，如果真的需要考慮大數的情況應該返回 vector<string>。）
4. 經過上面三步僅僅處理完了高位0~9中的一種情況，接下來應該改變高位的值，重復上述步驟，直至處理完高位為9的情況，才真正完成了整個全排列的流程。

---

代碼

class Solution {vector<int> iv;void dfs(int n, int digit, string& s){if(n == digit){ // 位數處理完畢int val = std::stoi(s);if(val){iv.push_back(val); }return;}for(int i = 0; i < 10; i++){s[digit] = i + '0'; // int -> chardfs(n, digit+1, s);}}
public:vector<int> printNumbers(int n) {string s(n, '0');dfs(n, 0, s);return iv;}
};