---

題目

輸入兩棵二叉樹A和B，判斷B是不是A的子結構。(約定空樹不是任意一個樹的子結構)

B是A的子結構， 即 A中有出現和B相同的結構和節點值。

例如:
給定的樹 A:

給定的樹 B：

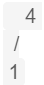
返回 true，因為 B 與 A 的一個子樹擁有相同的結構和節點值。

示例 1：

輸入：A = [1,2,3], B = [3,1]
輸出：false

示例 2：

輸入：A = [3,4,5,1,2], B = [4,1]
輸出：true

限制：

0 <= 節點個數 <= 10000

---

深搜

深搜思想主要是：

1. 根據先序遍歷先尋找與B相等的節點nA
2. 再判斷以nA為根節點的樹是否和B樹相吻合

算法流程：

函數 bool dfs(TreeNode* A, TreeNode* B); ：

1. 終止條件：

1. 當節點 B 為空：說明樹 B 已匹配完成，因此返回 true ；
2. 當節點 A 為空但節點 B 不為空：說明已經越過樹 A 葉子節點，即匹配失敗，返回 false ；
3. 當節點 A 和 B 的值不同：說明匹配失敗，返回 false ；

2. 返回值：

1. 判斷 A 和 B 的左子節點是否相等，即 dfs(A->left, B->left) ；
2. 判斷 A 和 B 的右子節點是否相等，即 dfs(A->right, B->right) ；

函數 isSubStructure(TreeNode* A, TreeNode* B) ：

1. 特例處理： 當 樹 A 為空 或 樹 B 為空 時，直接返回 false ；
2. 返回值： 當 B 樹是 A 的子樹時，其必須滿足以下三個條件之一：

1. 以 A為根節點的樹包含 B 樹
2. 以 A的左子樹為根節點 的樹包含 B 樹
3. 以 A的右子樹為根節點 的樹包含 B 樹

上面 2. 3. 的實質就是在對樹 A 做先序遍歷。

復雜度分析：

1. 時間復雜度 O(MN) ： 其中 M,N 分別為樹 A 和 樹 B 的節點數量；先序遍歷樹 A 占用 O(M) ，每次調用 dfs(A, B) 判斷占用 O(N) 。
2. 空間復雜度 O(M) ： 當樹 A 和樹 B 都退化為鏈表時，遞歸調用深度最大。當 M≤N 時，遍歷樹 A 與遞歸判斷的總遞歸深度為 M ；當 M>N 時，最差情況為遍歷至樹 A 葉子節點，此時總遞歸深度為 M。

---

深搜代碼

class Solution {public:bool dfs(TreeNode* A, TreeNode* B){if(B==nullptr){return true;}if(A==nullptr || A->val != B->val) return false;return dfs(A->left, B->left) && dfs(A->right, B->right);}bool isSubStructure(TreeNode* A, TreeNode* B) {if(A == nullptr || B == nullptr){return false;}bool res = false;if(A->val == B->val){res = dfs(A, B);}if(res){return res;}return isSubStructure(A->left, B) || isSubStructure(A->right, B);}
};

簡化版本：

class Solution {
public:bool dfs(TreeNode* A, TreeNode* B){if(B==nullptr) return true;if(A==nullptr || A->val != B->val) return false;return dfs(A->left, B->left) && dfs(A->right, B->right);}bool isSubStructure(TreeNode* A, TreeNode* B) {return  (A != NULL && B != NULL) && (dfs(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B));}
};

---

廣搜

廣搜思想中也有 判定 nA為根節點 的樹與 B 樹是否吻合 的部分，因此其對應的函數和深搜中起到該作用的函數是一致的，無需更改。

不一樣的是 深搜用遞歸的的方法實現先序遍歷，而 廣搜用隊列來實現層序遍歷。

也就是說，廣搜思想主要是：

1. 根據層序遍歷先尋找與B相等的節點nA
2. 再判斷以nA為根節點的樹是否和B樹相吻合

算法流程：

函數bool bfs(TreeNode* A, TreeNode* B); 和深搜部分一樣，就不再贅述了。

函數 isSubStructure(TreeNode* A, TreeNode* B); ：

1. 特例處理： 當 樹 A 為空 或 樹 B 為空 時，直接返回 false ；
2. 隊列實現層序遍歷：

1. 先將 A 入隊
2. 當隊列不為空時：
   1. 將隊列中的元素依次彈出，判斷其與 B 是否相等。
   2. 相等則判斷以nA為根節點的樹是否吻合 B 樹，吻合則直接返回。
   3. 不吻合則判斷彈出的元素左右子樹是否為空，不為空則入隊。

廣搜代碼

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution { 	
public:bool bfs(TreeNode* A, TreeNode* B){if(B==nullptr) return true;if(A==nullptr || A->val != B->val) return false;return bfs(A->left, B->left) && bfs(A->right, B->right);}bool isSubStructure(TreeNode* A, TreeNode* B) {if(A == nullptr || B == nullptr){return false;}bool res = false;queue<TreeNode*> q;q.push(A);while(!q.empty()){size_t qs = q.size();for(size_t i = 0; i < qs; i++){auto node = q.front();q.pop();if(node->val == B->val){res = bfs(node, B);}if(res){return res;}if(node->left) q.push(node->left);if(node->right) q.push(node->right);}}return res;}
};