文章目錄
- 樹狀數組概念
- 前綴和和區間和
- 樹狀數組原理
- 區間和——單點更新
- 前綴和——區間查詢
- 完整代碼
- 離散化
- sort函數
- unique函數去重
- erase函數僅保留不重復元素
- 通過樹狀數組求逆序對
樹狀數組概念
樹狀數組又名二叉索引樹,其查詢與插入的復雜度都為 O(logN),其具有以下特征:
- 樹狀數組是一種實現了高效查詢「前綴和」與「單點更新」操作的數據結構。
- 是求逆序對的經典做法。
- 不能解決數組有增加和修改的問題。
前綴和和區間和
既然樹狀數組是為了解決前綴和問題,那么我們首先要知道什么是前綴和?
要提前綴和就不得不提區間和,舉個例子來說明兩者:
ivec = {1, 2, 3, 4}
presum = {1, 3, 6, 10} // 前綴和
sumrange[1,3] = 9 // 下標1~3的區間和,2+3+4=9
由上可得,sumrange[beg, end] = presum[end] - presum[beg - 1] ,以例子來分析其合理性:
因為 sumrange[1,3] = 2+3+4 ,presum[3] = 1+2+3+4 ,也就是說 sumrange[1,3] = presum[3] - ivec[0] ,ivec[0] = presum[0] = presum[1-1] ,因此, sumrange[1,3] = presum[3] + presum[0] 。
但 sumrange[beg, end] = presum[end] - presum[beg - 1] 有個隱患——訪問 beg-1 的位置容易導致下標越界,如:sumrange[0,4] 。因此我們可以改變前綴和數組下標 i 保存的內容,當有訪問越界風險時,前綴和數組下標 i 保存的是 [0, i] 的累加和;那么如果令 前綴和數組下標 i 保存 [0, i) 的累加和 ,令 presum[0] = 0 ,則可得到 sumrange[beg, end] = presum[end+1] - presum[beg] 。避免了下標越界的風險。
舉例為證:
ivec = {1, 2, 3, 4}
presum = {0, 1, 3, 6, 10}
sumrange[1,3] = presum[3+1] - presum[1] = 10 - 1 = 9
sumrange[0,3] = presum[3+1] - presum[0] = 10 - 0 = 10
明晰了如何通過前綴和數組來算區間和,那么實際上樹狀數組實現的就是如何用區間和算前綴和。
樹狀數組原理
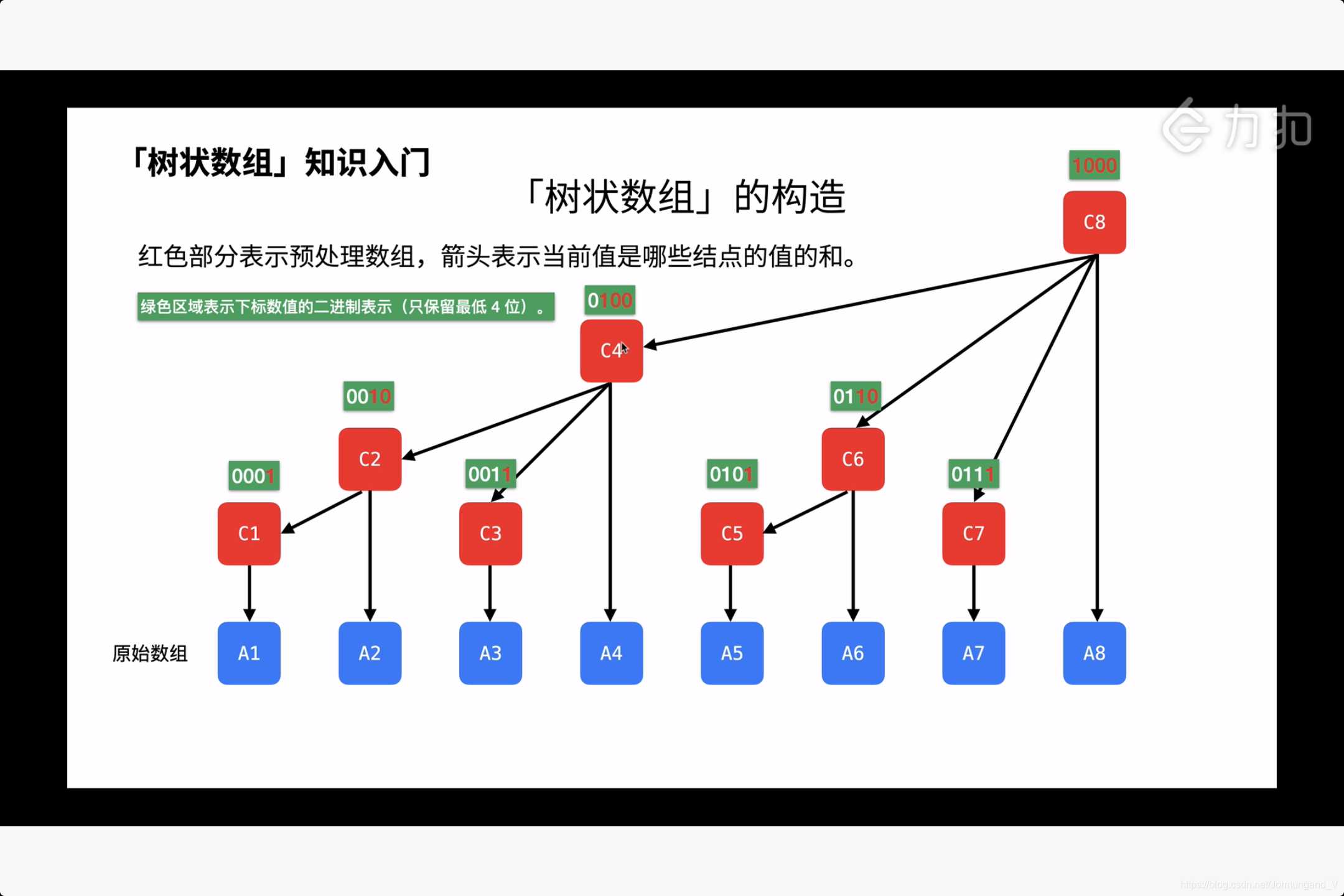
樹狀數組本質上是 空間換時間 的操作,保存 區間和 以求更快的算出 前綴和。以下圖為例,紅色數組為樹狀數組(稱為C),藍色數組為普通數組(稱為A)。由于上面證明了從 1 開始存儲可以避免訪問越界的情況。另,也因為在計算前綴和時,終止條件通常為遇0。 因此 A 和 C 都是從 1 開始存儲元素。
區間和——單點更新
樹狀數組是如何保存 區間和 的呢?通過觀察上圖,我們可以得到如下規律:
C1 = A1 = sumrange[1]
C2 = C1 + A2 = A1 + A2 = sumrange[1, 2]
C3 = A3 = sumrange[3]
C4 = C2 + C3 + A4 = A1 + A2 + A3 + A4 = sumrange[1, 4]
C5 = A5 = sumrange[5]
C6 = C5 + A6 = A5 + A6 = sumrange[5, 6]
C7 = A7 = sumrange[7]
C8 = C4 + C6 + C7 + A8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 = sumrange[1, 8]
以上規律可以總結歸納為這樣的特征:下標 i 存儲了從 i 往前 2k (k為二進制表示的 i 中 末尾0 的個數)個元素的區間和(出現次數),舉例驗證:
i = 8 = 1000, k = 3, 2^3 = 8, C8 是 A1~A8 的區間和(出現次數)
i = 6 = 110, k = 1, 2^1 = 2, C6 是 A5~A6 的區間和(出現次數)
i = 5 = 101, k = 0, 2^0 = 1, C5 是 A5 的區間和(出現次數)
怎樣實現這樣的存儲方式呢?對于一個輸入的數組A,我們每一次讀取的過程,其實就是一個不斷更新單點值的過程,一邊讀入 A[i] ,一邊將 C[i] 涉及到的祖先節點值更新,完成輸入后樹狀數組也就建立成功了。舉個例子:
假設更新 A[2] = 8 ,那么管轄 A[2] 的 C[2],C[4],C[8] 都要加上 8(A2 的所有祖先節點),那么怎么找到所有的祖先節點呢?通過觀察他們的二進制形式我們發現:
- C2 = C10 ; C4 = C100 ; C8 = C1000
不明顯,再觀察一個一個例子,A[5] 的祖先節點有 C[5],C[6],C[8] ,觀察其二進制形式:
- C5 = C101 ; C6 = C110 ; C8 = C1000
也就是說,我們不斷地對 二進制i 的 末尾1 進行 +1 操作(尋找末尾1由Lowbit函數實現),直至到達 樹狀數組下標最大值 n 。
實現單點更新update(i, v):把下標 i 位置的數加上一個值 v 。
int Lowbit(int x){return x & -x;
}void update(int i, int v){while(i<=n){ // n為樹狀數組.size()-1tree[i] += v;i += Lowbit(i);}
}
PS:在求逆序對的題目中,C[i] 保存某一區間元素出現的次數,便于快速計算前綴和。
前綴和——區間查詢
如何通過 區間和 得到 前綴和 ?舉例說明:
presum[8] = C8。8 = 1000presum[7] = C7 + C6 + C4。7 = 111,6 = 110,4 = 100presum[5] = C5 + C4。5 = 101,4 = 100
對于 presum[i] 而言,結合著后面跟的二進制表示,不難發現,求 presum[i] 即是將 i 轉換為 二進制 ,不斷對 末尾的1 進行 -1 的操作(尋找末尾1由Lowbit函數實現),直到全部為0停止。
?
實現區間查詢函數 query(i): 查詢序列 [1?i] 區間的區間和,即 i 位置的前綴和。
PS:在求逆序對的題目中,i-1 位的前綴和 presum[i-1] 表示「有多少個數比 i 小」,也就代表了有多少個逆序對。
int query(int i){int res = 0;while(i > 0){res += tree[i];i -= Lowbit(i);}return res;
}
完整代碼
class BIT {vector<int> tree;int len;
public:BIT(int n):len(n), tree(n){}BIT(vector<int>& nums>{len = nums.size();tree = vector<int>(nums.size()+1);} static int Lowbit(int x){return x & -x;}int query(int x){ // 區間查詢int res = 0;while(x){res += tree[x];x -= Lowbit(x);}return res;}void update(int x){ // 單點更新while(x<len){tree[x]++;x += Lowbit(x);}}
};
離散化
離散化常常用在通過樹狀數組求逆序對的題目中,連續化時,樹狀數組的長度為普通數組的最大元素。
比如題目給出一個數組 ivec = { 7, 4, 5, 100, 7, 5 } ,通過樹狀數組求逆序對的步驟如下:
- 創建長度為
100的樹狀數組,下標從1開始。 - 倒序遍歷
ivec,通過區域求和得到tree數組中下標ivec[i]的前綴和,前綴和代表著比ivec[i]小的元素有幾個。 - 更新單點,執行
tree[ivec[i]]++。舉例:ivec[i]=7,tree[7]++,代表7已被遍歷過,出現了一次。
具體執行:
res = 0; // 存儲逆序對個數
ivec = { 7, 4, 5, 100, 7, 5 }^
0 0 0 0 1 1 0 1 0 …… 0
1 2 3 4 5 6 7 8 9 …… 100
執行 res += query(4) 【已有的小于ivec[i]的元素才構成逆序對,因此從 ivec[i]-1 開始區間查詢】得到 res = 0 + 0 = 0
單點更新,下標為 5、6、8…… 的 value 加 1ivec = { 7, 4, 5, 100, 7, 5 }^
0 0 0 0 1 1 1 2 0 …… 0
1 2 3 4 5 6 7 8 9 …… 100
執行 res += query(6) 得到 res = 0 + 1 = 1
單點更新,下標為 7、8…… 的 value 加 1ivec = { 7, 4, 5, 100, 7, 5 }^
0 0 0 0 1 1 1 2 0 …… 1
1 2 3 4 5 6 7 8 9 …… 100
執行 res += query(99) 得到 res = 1 + 1 = 2
單點更新,下標為 100 的 value 加 1ivec = { 7, 4, 5, 100, 7, 5 }^
0 0 0 0 2 2 1 3 0 …… 1
1 2 3 4 5 6 7 8 9 …… 100
執行 res += query(4) 得到 res = 2 + 0 = 2
單點更新,下標為 5、6、8…… 的 value 加 1
以此類推,很容易算出逆序對的數量。但是!可以發現1、2、3、6、8、9、…… 、98、99這些絕大多數位置都浪費了。因此我們需要對樹狀數組離散化,以節省內存空間。
實現樹狀數組離散化:
void Discretization(vector<int>& nums) {// nums 是 輸入數組 的拷貝數組sort(nums.begin(), nums.end());nums.erase(unique(nums.begin(), nums.end()), nums.end()); //元素去重,下文有詳細剖析
}int getid(int x, vector<int> nums){return lower_bound(nums.begin(), nums.end(), x) - nums.begin() + 1;
}
上述代碼的作用簡單來講就是,通過 Discretization函數 將 nums 中的值保存到 a 中,并進行升序排列、元素去重的操作。以 ivec 為例,經過 Discretization函數 處理,得到
a = {4, 5, 7, 100}
而通過 getid函數 將 a 中元素映射為對應的樹狀數組下標,也就是 4 存在樹狀數組下標為 1 的地方,5 存在樹狀數組下標為 2 的地方……以此類推。舉例:
ivec = { 7, 4, 5, 100, 7, 5 }^
0 1 0 1 // value
4 5 7 100 // 映射得到的邏輯下標
1 2 3 4// 物理下標
執行 res += query(getid(5)) 得到 res = 0
單點更新,下標為 getid(5)=2、getid(100)=4 的 value 加 1ivec = { 7, 4, 5, 100, 7, 5 }^
0 1 1 2 // value
4 5 7 100 // 映射得到的邏輯下標
1 2 3 4// 物理下標
執行 res += query(getid(7)) 得到 res = 1
單點更新,下標為 getid(7)=3、getid(100)=4 的 value 加 1
下面是對 Discretization函數 的剖析。
sort函數
- 接受兩個迭代器,表示要排序的元素范圍
- 是利用元素類型的<運算符實現排序的,即默認升序
實例:

unique函數去重
- 重排輸入序列,將相鄰的重復項“消除”;
- “消除”實際上是把重復的元素都放在序列尾部,然后返回一個指向不重復范圍末尾的迭代器。
實例:
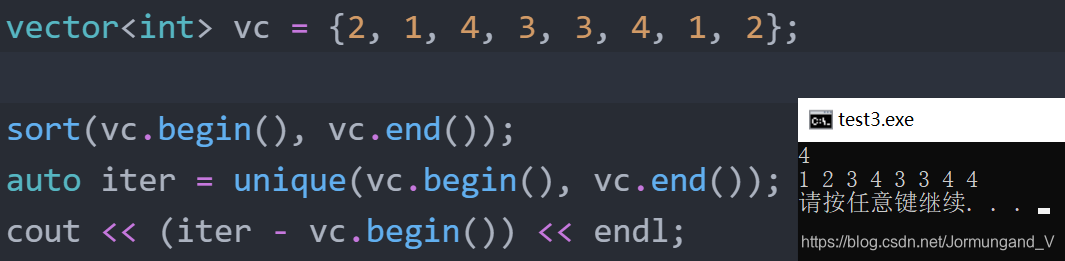
從上圖可知,unique返回的迭代器對應的vc下標為4,vc的大小并未改變,仍有10個元素,但順序發生了變化,相鄰的重復元素被不重復元素覆蓋了, 原序列中的“1 2 2”被“2 3 4”覆蓋,不重復元素出現在序列開始部分。
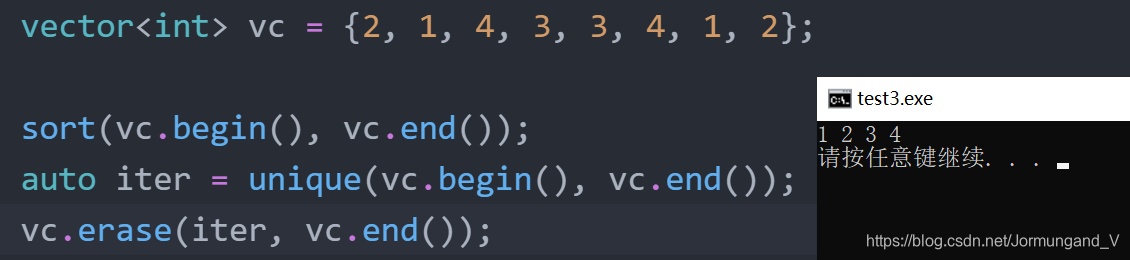
erase函數僅保留不重復元素
可以通過使用容器操作——erase刪除從end_unique開始直至容器末尾的范圍內的所有元素:
通過樹狀數組求逆序對
題源力扣:數組中的逆序對
代碼實現:
class BIT {vector<int> tree;int st;
public:BIT(int n) :st(n), tree(n) {}BIT(vector<int>& nums) {st = nums.size();tree = vector<int>(nums.size());for (int i = 0; i < nums.size(); i++) {update(i, nums[i]);}}static int Lowbit(int x) {return x & -x;}int query(int x) { // 區間查詢int res = 0;while (x) {res += tree[x];x -= Lowbit(x);}return res;}void update(int x, int v) { // 單點更新while (x < st) {tree[x] += v;x += Lowbit(x);}}void show() {for (int i : tree) {cout << i << " ";}cout << endl;cout << " 4 5 7 100" << endl;}
};
class Solution {void Discretization(vector<int>& tmp) {sort(tmp.begin(), tmp.end());tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end()); //元素去重}int getid(int x, vector<int>& tmp) {return lower_bound(tmp.begin(), tmp.end(), x) - tmp.begin() + 1;}
public:int reversePairs(vector<int>& nums) {int n = nums.size();vector<int> tmp = nums; // tmp作為離散化數組Discretization(tmp); // 排序去重BIT bit(tmp.size()+1);//bit.show();int res = 0; // 逆序對個數for (int i = n - 1; i >= 0; i--) {//cout << "v[i]: " << nums[i] << endl;int id = getid(nums[i], tmp); // 尋找映射res += bit.query(id - 1);// 因為計算的是value小于nums[i]元素的數目// 因此從前一位開始,下標id保存的是當前value=nums[i]的個數bit.update(id, 1); // nums[i]的個數+1//bit.show();//cout << "res: " << res << endl;}return res;}
};int main() {vector<int> v = { 7, 4, 5, 100, 7, 5 };Solution s;/*int res = s.reversePairs(v);cout << res << endl;*/cout << s.reversePairs(v) << endl;
}
/*
7, 4, 5, 100, 7, 5
*/








、進程地址空間)


調用))
【標準流和其文件描述符、fwrite函數、perror函數】)






