---

題目

數字以0123456789101112131415…的格式序列化到一個字符序列中。在這個序列中，第5位（從下標0開始計數）是5，第13位是1，第19位是4，等等。

請寫一個函數，求任意第n位對應的數字。

---

思路

我們注意到，如果：

1. 將 01234567891? 中的每一位稱為 位 ，記為 n ；
2. 將 10,11,12,? 稱為 數字 ，記為 num ；
3. 數字 10 是一個兩位數，稱此數字的 位數 為 2 ，記為 digit ；
4. 每 digit 位數的起始數字（即：1,10,100,?），記為 start 。
5. 個位數共有 1 ~ 9 九個數字，稱個位數的 數字數量 為 9 ，記為 num_count 。
6. 十位數共有 10~99 90個數字，每個數字有兩位，共占序列化 90*2=180 位，稱十位數的 數位數量 為 180 ， 記為 count 。

可以得到下表（個位數不計入0）：

數字范圍	位數	數字數量	共占序列化多少位
1~9	1	9	9
10~99	2	90	180
100~999	3	900	2700
……	……	……	……
start~end	digit	9*start	9 * start * digit

可以得到三個公式：

1. 位數遞推公式 digit = digit + 1
2. 起始數字遞推公式 start= start * 10
3. 數字數量計算公式 num_count = 9 * start
4. 數位數量計算公式 count = 9 * start * digit

我們可以將求 第n位對應的數字 求解過程分為以下幾步：

1. 確定 n 所在 數字 的 位數digit ；
2. 確定 n 所在的 數字num ；
3. 確定 n 是 num 中的哪一位。

第一步：

在幾位數的范圍內？

while(n>count){n -= count;start *= 10;digit++;count = 9*start*digit;
}

第二步：

是哪個數字？

int num = start+(n-1)/digit;

為什么是 (n-1)/digit 而不是 n/digit ？

首先看一張圖：

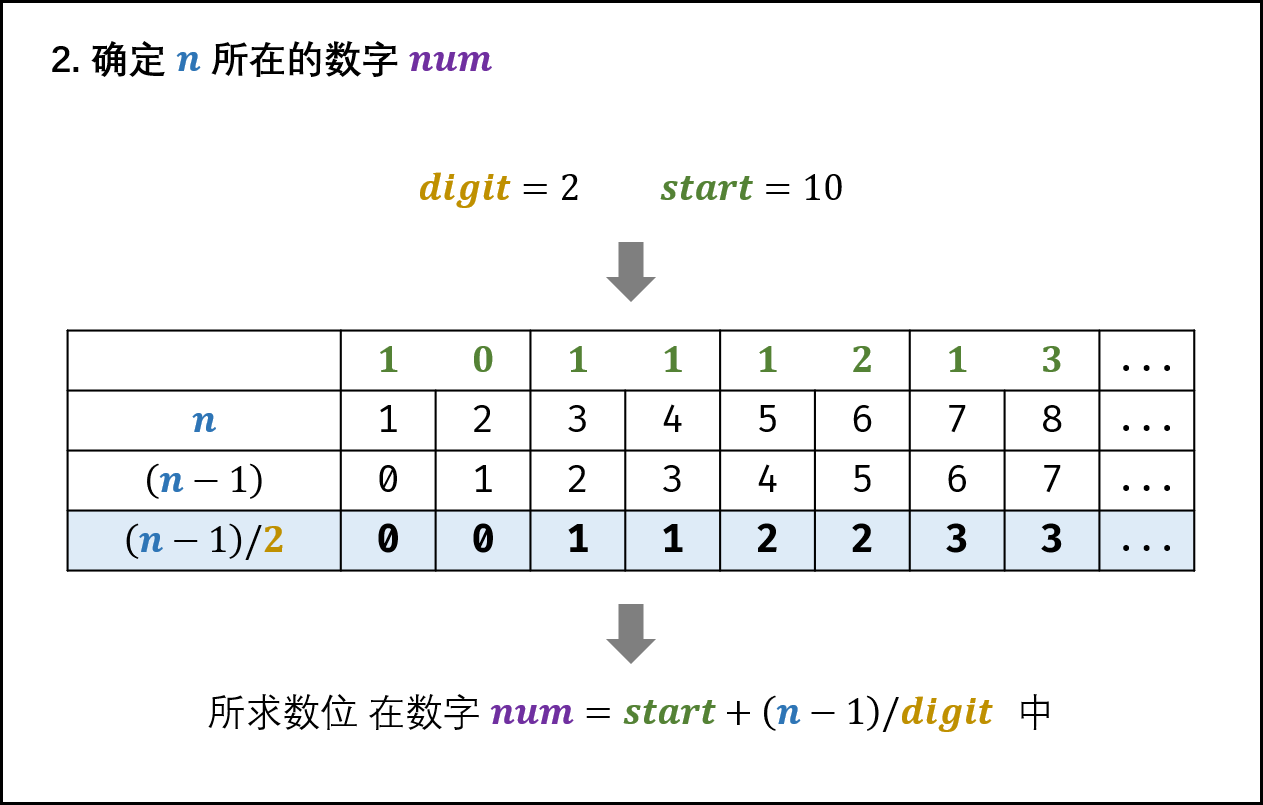
以兩位數為例，當執行完 n=n-9 之后，n 與各個兩位數數位的對應關系如上圖所示。以13為例，當我們知道 n=7（13中的1） 時，由 n/2=3 可得 n 是十位數起始數字之后的第三個，但是當 n=8（13中的3） 時，由 n/2=4 得到 n 對應的是十位數起始數字之后的第四個，這是錯誤的，十位數起始數字之后的第四個是 14 而非 13 ，因此計算時需要將 n 進行 減一操作，因為我們將起始數字看作 第0個數 而非 第1個數 。

為什么是 (n-1)/digit 而不是 n/digit-1？

仍然以兩位數為例，當 n 對應非起始數字時，兩種算法是沒有區別的，但是當 n 對應起始數字時，不論 n=0 or n=1 ， (n-1)/digit 的計算結果都為 0 ，而 n/digit-1 的計算結果都為 -1 。 (n-1)/digit 對應的數字 num = start + 0 = 10 ，正確；而 n/digit-1 對應的數字 num = start + (-1) = 9 ，變成了個位數，錯誤。

總而言之，對 n 進行 減一操作 是因為 起始數字應視為 start + 0，雖然它是兩位數里面的 第一個 數字，但是我們在公式里說的 第幾個 是 該數字相對于起始數字 而言的，因此要統統減一。而之所以不是 先除再減 而是 先減再除 是因為 要考慮邏輯順序對起始數字的影響 。

第三步：

處于對應數字的哪一位？

num = s[(n-1)%digit] - '0';

(n-1)%digit 計算的便是對應的 數位 ，n減一的原因和第二步中相同，不再贅述。

---

代碼

class Solution {
public:int findNthDigit(int n) {long long start=1, count=9, digit=1;while(n>count){n -= count;start *= 10;digit++;count = 9*start*digit;}int num = start+(n-1)/digit;//所在數字string s = to_string(num);num = s[(n-1)%digit] - '0';//處于所在num的哪一位return num;}
};

---

復雜度分析

時間復雜度 O(logn) ： 所求數位 n 對應數字 num 的位數 digit 最大為 O(log n) ；第一步最多循環 O(log n) 次；第三步中將 num 轉化為字符串使用 O(log n) 時間；因此總體為 O(log n) 。

空間復雜度 O(logn) ： 將數字 num 轉化為字符串 str(num) ，占用 O(logn) 的額外空間。

---

致謝

思路中的部分想法、復雜度分析源于K神的題解，鞠躬致謝。