---

題目

請實現一個函數用來匹配包含 . 和 * 的正則表達式。模式中的字符 . 表示任意一個字符，而 * 表示它前面的字符可以出現任意次（含0次）。在本題中，匹配是指字符串的所有字符匹配整個模式。例如，字符串 aaa 與模式 a.a 和 ab*ac*a 匹配，但與 aa.a 和 ab*a 均不匹配。

來源：力扣（LeetCode）

---

思路

再一次膜拜大佬 作者：jyd
本文基于大佬的思路做自己的細節解析。

其實動規的難點一直在于“找規律”。（恐怕這也是所有算法題的難點，哈哈）

本題其實就是在考察程序員思考問題的全面性。

轉移方程

先建立這道題的轉移方程：

用 f[i][j] 代表 s 的前 i 個和 p 的前 j 個能否匹配。

當正則表達式中為 正常字符 和 . 時，問題是很好解決的：

f[i][j]=f[i?1][j?1]

前 i 個 s 和 前 j 個 p 是否匹配還要看 前 i-1 個 s 和 前 j-1 個 p 是否匹配。

難點就在于是 字符 + * 時該怎么處理：

分為將字符看成 出現0次（也就是不看這兩位）和 出現多次（看這個組合）：

• 不看：直接砍掉正則串的后面兩個， f[i][j] = f[i][j-2]
• 看：正則串不動，主串前移一個，f[i][j] = f[i-1][j]

上面兩點，大部分題解已經說的很明白了，但其實又很抽象。我們不妨用例子來看一下：

• 第一種比較好理解 —— f[i][j] = f[i][j-2]

s=abcd
p=abcde*

將主串的最后一位視為 i（a），正則串最后一位視為 j（*）。顯而易見兩個字符串是完全匹配的。只需要 * 前面的 e（j-1） 出現0次就可（正則串里面的 d 就是 j-2）。

• 第二種理解起來可能有點抽象 —— f[i][j] = f[i-1][j]

s=abccc
p=abc*

此時 i為c 、j為*，因為 *前面的字符 可以 出現多次，也就是出現1次的遞歸操作。因此此時我們做的操作就是：

• 已經知道了 i 是 j（也就是*前的字符） ，那么再試著看看 i-1 還是不是 j。

也就是原本相互匹配的字符我們不看了（都做-1操作），i 和 j 彼此是匹配的，理應再看 i-1 和 j-1，但是我們想要 j 多出現幾次，因此 j-1 的操作沒有執行。這就是下圖中，jyd大佬所說的 p[j-2]多出現1次。

圖中總說 s[i-1] p[j-1] 為什么不是直接用 s[i] p[j] 呢？這個問題講完初始化dp數組首行我們再細說。

特征

弄懂了主要的驗證是否匹配的操作，接下來我們需要弄懂一些特例：

首先明晰一點：正則串和主串都是可以為空串的。

• 空主串和空正則是匹配的。
• 非空串和空正則必不匹配。
• 空主串和非空正則，不能直接判定匹配與否。
• 非空串和非空正則，那肯定是需要計算的了。

我們可以根據上面的特征，來初始化dp二維數組。

行代表s，列代表p，dp[0][j] 代表s為空，dp[i][0]代表p為空。

第四點其實就是我們的轉移方程。因此我們來詳解一下第三點：

當s= '' '' 時，p=a*b*c* 和 p=ab* 前者可以做到和空主串完美匹配，后者卻不行。因此我們可以得出以下規律：

因此可以得到初始化dp首行的代碼（首列無需做多余更改，空正則除了匹配空主串，其余皆不匹配）：

// 初始化dp首行
dp[0][0] = 1;
for(size_t i = 2; i < cols; i += 2){dp[0][i] = dp[0][i-2] && p[i-1] =='*';
}

---

再探 i 和 j

我讀完大佬寫的題解的時候其實還是很懵懂的，真正豁然開朗是看了大佬的圖解。大佬做圖解一直有一手的~

下面結合圖解來講一下我們遺留的問題，dp[i][j] 和與之相對應的 s[i-1] p[j-1]。

我們借用一下大佬的圖來看一下：

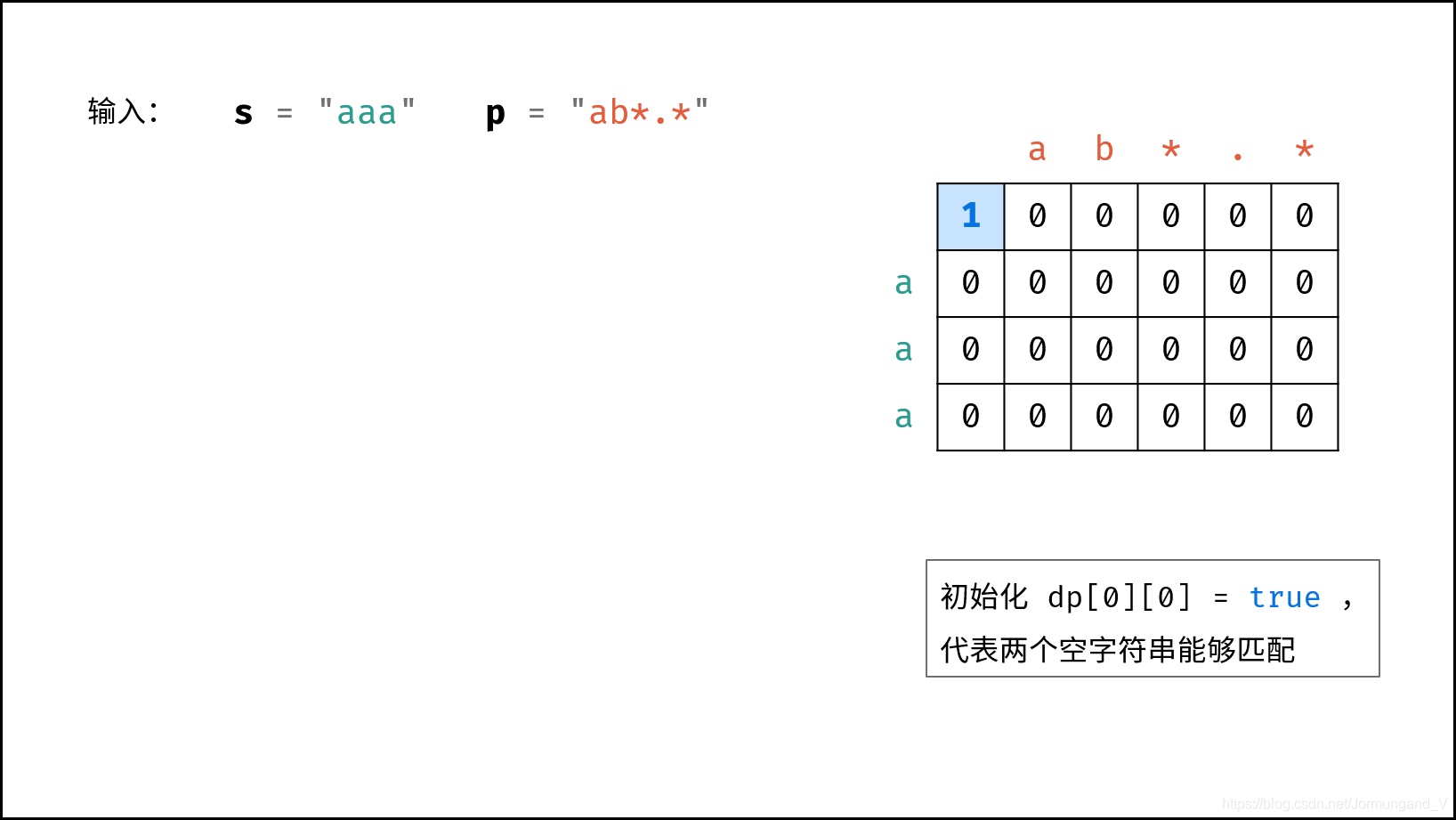
我們會發現，前面提到：

• 第一行，也就是下標為0的那行，代表 s 為空串
• 第一列，也就是下標為0的那列，代表 p 為空串

我們是從第二行（下標為1的行）和第二列（下標為1的列）開始保存 s 和 p 的非空部分的。

因此，舉個具體的例子：dp[1][1]其邏輯含義是，保存的值表示 前1個s 和前1個p 是否匹配。在物理上代表 s[0] 和 p[0] 組成的點。因此我們也就不難理解大佬圖解中頻繁出現的 dp[i][j] 和 s[i-1] p[j-1] 之間的關系了。

---

代碼

class Solution {
public:bool isMatch(string s, string p) {int rows = s.size()+1;int cols = p.size()+1;vector<vector<int>> dp(rows, vector<int>(cols, 0));// 初始化dp首行dp[0][0] = 1;for(size_t i = 2; i < cols; i += 2){dp[0][i] = dp[0][i-2] && p[i-1] =='*';}// 動規for(size_t i = 1; i < rows; i++){for(size_t j = 1; j < cols; j++){if(p[j-1] != '*'){if(dp[i-1][j-1] && (s[i-1]==p[j-1] || p[j-1] == '.')){dp[i][j] = 1;}}else{if(dp[i][j-2] || (dp[i-1][j] && (s[i-1] == p[j-2] || p[j-2] == '.'))){dp[i][j] = 1;}}}}return dp[rows-1][cols-1];}
};