---

題目

給一個只循環遞增一次的數組 res，res 滿足首元素大于等于尾元素，形如：

4，5，6，7，2，4

再給出一個整型數字 num，將其插入到數組中應在的位置。

示例：

輸入：

res = 4，5，6，7，2，4
num = 3

輸出：

4，5，6，7，2，3，4

---

思路

用二分查找確定應該插入的位置，難點在于左右區間的建立。

如何建立左右區間？

首先明確兩點，對于整個數組而言：

• 首元素一定 大于等于 尾元素
• 以數組的最大值為界限，最大值左邊的元素一定 大于等于 右邊的元素

用圖像表示數組是這樣的（黑色表下標，紫色表值）：

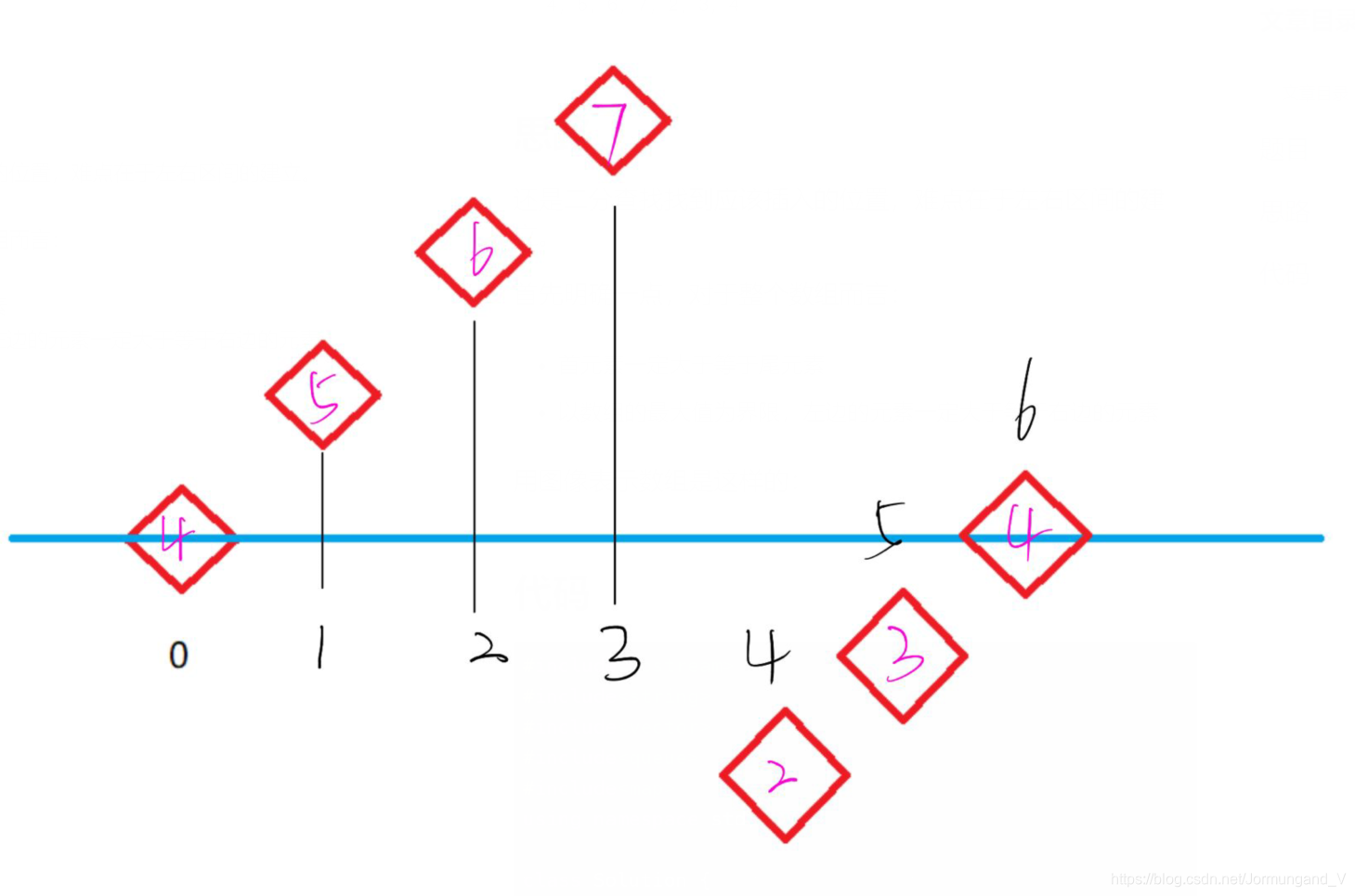
我們可以看到，要插入的元素無非在最高點的左邊或右邊（自下文始，最高點用high替代，首元素位置用begin表示，尾元素位置用last表示）：

• 當 num 處于最高點左邊時，二分查找的范圍應該是 [begin, high]
• 當 num 處于最高點右邊時，二分查找的范圍應該是 [high+1，last]

也就是說，劃定二分查找范圍（左右區間的建立）的重中之重在于最高點的確定。

如何查找最高點？

個人想到兩種方法：

• 遍歷查找，時間復雜度O(n)

算法思想沒有什么多說的，中規中矩的遍歷。

int high = 0;
for (int i = 1; i < res.size(); i++) {if (res[high] > res[i]) {break;}high = i;
}

• 二分查找，時間復雜度O(log²n)

算法思想是:

1. 先以數組首元素、尾元素作為二分查找的左右邊界，中間元素暫定為high
2. 以 左邊界小于右邊界 作為while的循環條件
3. 首先判斷此時的high是否大于首元素
4. 大于首元素證明此時的high處于 真正最高點的左邊 或 就是真正最高點，此時需要判定high+1中元素和high中元素之間的關系：

1. 如果high+1中元素大于high中元素，表明 真正最高點應該在high的左邊，因此更新左邊界—— left = high + 1
2. 如果high+1中元素小于high中元素，表明 high即為真正最高點 ，因此break出while循環即可

5. 小于首元素證明此時的high處于 真正最高點的右邊 ，此時需要判定high和high-1所指元素之間的關系：

1. 如果 res[high - 1] < res[high] （如舉例中high=6時，4>3），表明最高點仍在 high-1的左邊，也就是high-1也處于真正最高點的右邊，因此要更新右邊界—— right = high - 2
2. 如果 res[high - 1] > res[high] ， 此時表明high-1即為最高點，因此將high–并break出while循環即可

6. 每次循環更新完左右邊界之后需要更新high值—— high = left + (right - left) / 2;
7. 跳出while循環得到的high即為最高點的位置

int size = res.size() - 1;
int left = 0;
int right = size;
int high = left + (right - left) / 2;
int flag = res[0];
while (left < right) {if (res[high] >= flag) {if (res[high + 1] > res[high]) {left = high + 1;}else {break;}}else {if (res[high - 1] < res[high]) {right = high - 2;}else {high--;break;}}high = left + (right - left) / 2;
}

那我們怎么判斷 num 到底處于什么樣的位置呢？

這時應該結合之前我們說到的一句話：

首元素一定 大于等于 尾元素

那我們做個歸納，如果：

1. num > res[0] ，num 處于 high 左邊
2. res[end] < num == res[0] ，num 處于 high 右邊，插入到尾元素的位置
3. res[end] == num == res[0] ，不可能出現這種情況，因為這種情況下num沒有位置可以插入。
4. res[end] == num < res[0] ，num 處于 high 左邊，插入到首元素的位置
5. res[end] > num ，num 處于 high 右邊

第二點和第四點是什么意思呢？

關于第二點，我們舉這樣一個例子：

輸入：

res = 5，6，7，2，4
num = 5

輸出：

res = 5，6，7，2，4，5

關于第四點，我們舉這樣一個例子：

輸入：

res = 6，7，2，4，5
num = 5

輸出：

res = 5，6，7，2，4，5

因此根據上面的歸納我們可以得到代碼：

注意：因為第三種情況不可能出現，因此我們在描述第2、4種情況時可以省略大小比較，因為當2、4種描述的等于關系成立時，大小關系必然成立。

if (res[size] > num || num == res[0]) { // num處于high右邊left = high + 1;right = size;
}
if(num > res[0] || num == res[size]) { // num處于high左邊left = 0;right = high;
} 

如何確定插入位置？

建立好左右邊界后就可以根據二分查找來確定插入位置了。

1. 當左邊界小于右邊界時執行二分查找。
2. 中間點（mid）對應的元素小于 num 時，左邊界更改為 mid+1 。
3. mid 對應的元素大于 num 時，右邊界更改為 mid-1 。

int mid = left + (right - left) / 2;
while (left <= right)
{if (res[mid] < num) {left = mid + 1; }else {right = mid - 1;}mid = left + (right - left) / 2;
} 

插入元素

最終使用insert函數進行插入：

res.insert(res.begin() + mid, num);

insert會將給定值插入到給定位置之前。

---

代碼

class Solution {
public:vector<int> fun(vector<int> res, int num) {int size = res.size() - 1;int left = 0;int right = size;/*int high = 0;for (int i = 1; i < res.size(); i++) {if (res[high] > res[i]) {break;}high = i;}*/// 與上面注釋部分一樣都是查最高點int high = left + (right - left) / 2;int flag = res[0];while (left < right) {if (res[high] > flag) {if (res[high + 1] > res[high]) {left = high + 1;}else {break;}}else {if (res[high - 1] < res[high]) {right = high - 2;}else {high--;break;}}high = left + (right - left) / 2;}// 確定左右邊界if (res[size] > num || num == res[0]) { // num處于high右邊left = high + 1;right = size;}if(num > res[0] || num == res[size]) { // num處于high左邊left = 0;right = high;} // 確定插入位置int mid = left + (right - left) / 2;while (left <= right){if (res[mid] < num) {left = mid + 1; }else {right = mid - 1;}mid = left + (right - left) / 2;} res.insert(res.begin() + mid, num);return res;}
};

用例測試：

int main() {Solution s;vector<int> iv = { 4,5,6,7,1,2,4 };int num = 3;iv = s.fun(iv, num);for (auto i = iv.begin(); i != iv.end(); i++) {cout << *i << " ";}cout << endl;
}