---

其他與排序有關的文章

一學就廢的三種簡單排序【冒泡、插入、選擇】

---

原理

歸并排序（Merge sort）： 歸并排序對元素 遞歸地 進行 逐層折半分組，然后從最小分組開始，逐層進行 比較排序 + 合并成一個大的分組 。

用一張圖表示其原理：

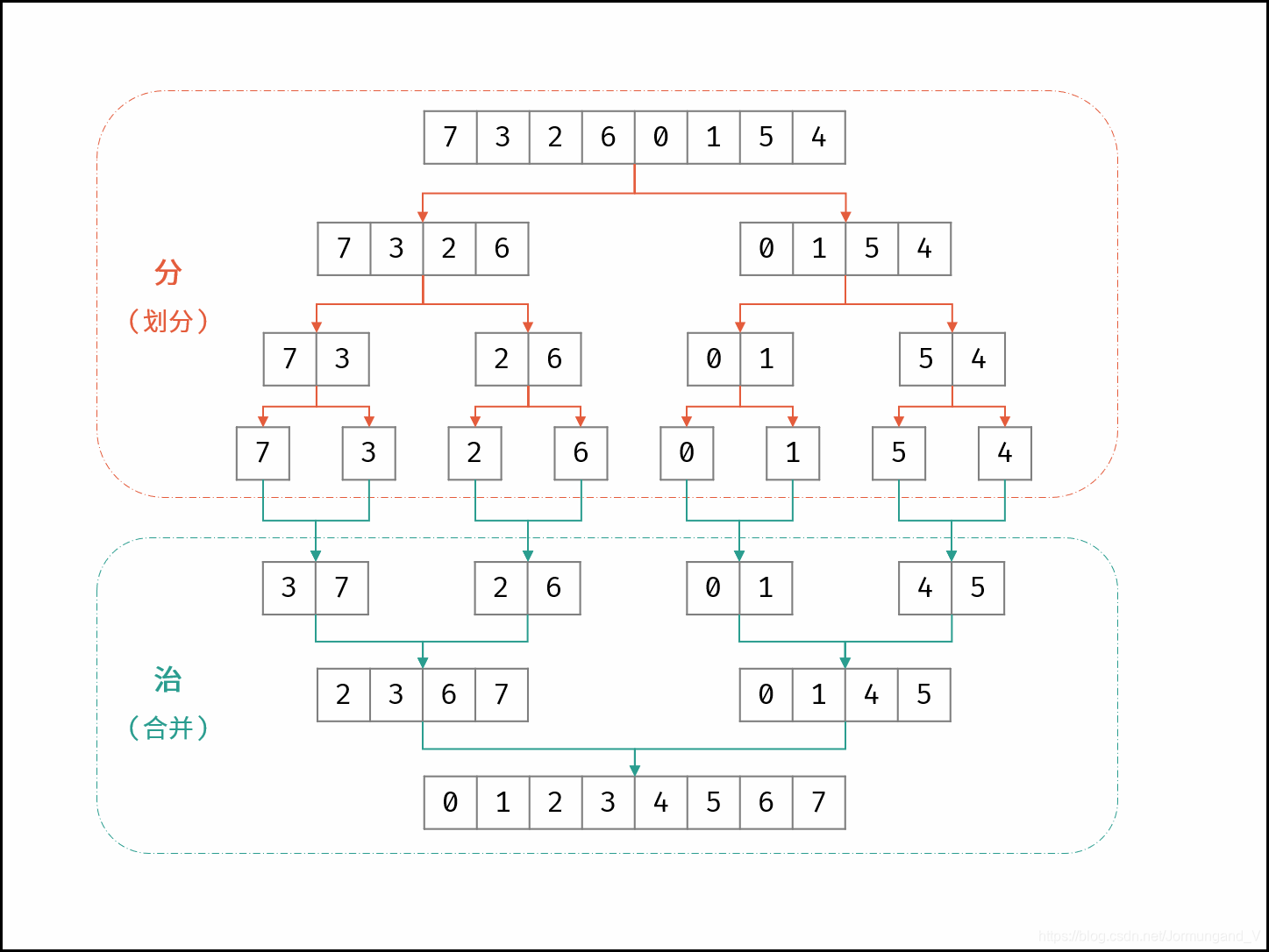
圖源Krahets

---

代碼實現

void Merge(vector<int>& nums, int left, int right){// 終止條件if(left >= right) return;// 遞歸拆分int mid = (left+right)/2;Merge(nums, left, mid);Merge(nums, mid+1, right);// 合并排序vector<int> tmp(right-left+1);// 新建臨時數組用以保存排序好的元素int i = left, j = mid + 1, p = 0;while(i<=mid && j<=right){ // 升序排列if(nums[i] < nums[j]) tmp[p++] = nums[i++];else tmp[p++] = nums[j++];}// 處理剩余左\右子數組元素while(i <= mid) tmp[p++] = nums[i++];while(j <= right) tmp[p++] = nums[j++];//結果儲存for(int i=0; i<tmp.size(); i++){nums[i + left] = tmp[i];}
}

可以進行優化，畢竟如果每次遞歸都新建一個tmp數組是很費時間的：

void Merge(vector<int>& nums, int left, int right, vector<int>& tmp){// 終止條件if(left >= right) return;// 遞歸拆分int mid = (left+right)/2;Merge(nums, left, mid, tmp);Merge(nums, mid+1, right, tmp);// 合并排序int i = left, j = mid + 1, p = left;while(i<=mid && j<=right){ // 升序排列if(nums[i] < nums[j]) tmp[p++] = nums[i++];else tmp[p++] = nums[j++];}// 處理剩余左\右子數組元素while(i <= mid) tmp[p++] = nums[i++];while(j <= right) tmp[p++] = nums[j++];//結果儲存for(int i=left; i<=right; i++){nums[i] = tmp[i];}
}

---

復雜度分析

• 時間復雜度 O(NlogN) ： 其中 N 為數組長度；歸并排序使用 O(NlogN) 時間；
• 空間復雜度 O(N)： 輔助數組 tmp 占用 O(N) 大小的額外空間；