一，直方圖的繪制

1.直方圖的概念：

在圖像處理中，經常用到直方圖，如顏色直方圖、灰度直方圖等。
圖像的灰度直方圖就描述了圖像中灰度分布情況，能夠很直觀的展示出圖像中各個灰度級所
占的多少。
圖像的灰度直方圖是灰度級的函數，描述的是圖像中具有該灰度級的像素的個數：其中，橫
坐標是灰度級，縱坐標是該灰度級出現的頻率。
（簡潔來說：就是描述圖像中各個灰度級的個數）

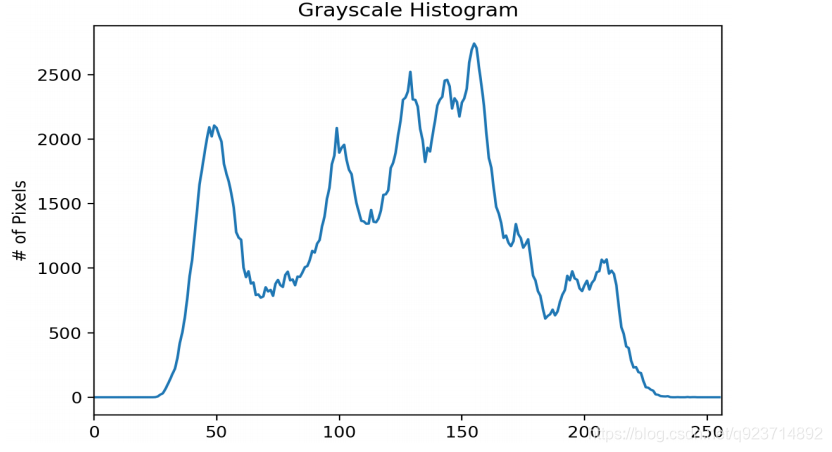
直方圖反映了圖像中的灰度分布規律。它描述每個灰度級具有的像素個數，但不包含
這些像素在圖像中的位置信息。
圖像直方圖不關心像素所處的空間位置，因此不受圖像旋轉和平移變化的影響，可以作為圖像的特征。

2.直方圖的應用：

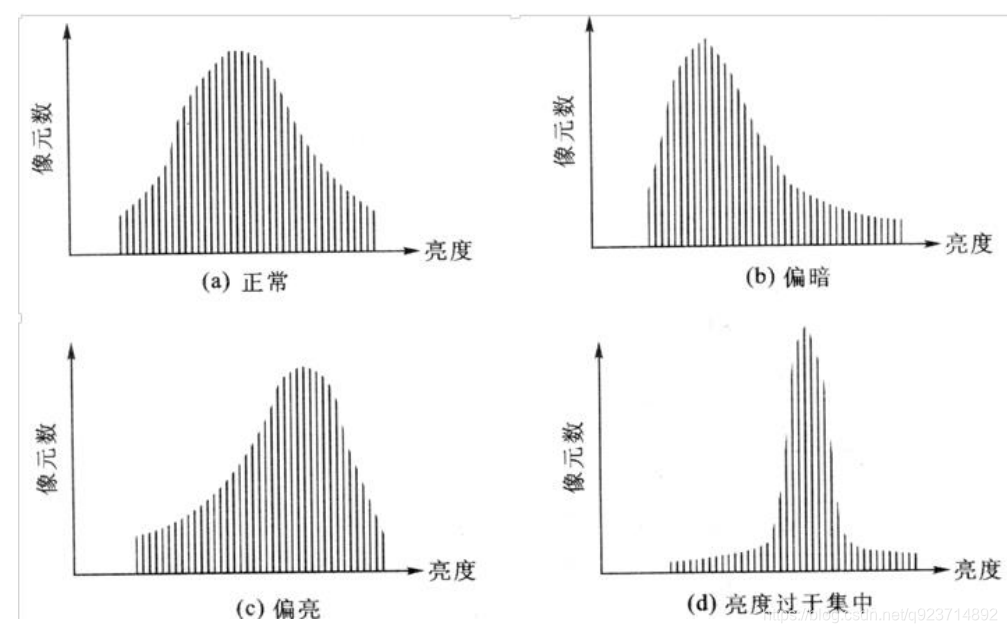
直方圖的應用主要體現在來表現圖像是否過亮或過暗，而解決的辦法就是直方圖均值化。

3.代碼實現：

1. 頭文件：

import cv2
import numpy as np
from matplotlib import pyplot as plt

2. 灰度圖像直方圖繪制：
   1. plt接口實現：

      # 獲取灰度圖像
      img = cv2.imread("lenna.png", 1)
      gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
      #cv2.imshow("image_gray", gray)# 灰度圖像的直方圖，方法一
      plt.figure()
      plt.hist(gray.ravel(), 256)
      plt.show()
      

   2. opencv接口實現：

      '''
      equalizeHist—直方圖均衡化
      函數原型： equalizeHist(src, dst=None)
      src：圖像矩陣(單通道圖像)
      dst：默認即可
      '''# 灰度圖像的直方圖, 方法二
      hist = cv2.calcHist([gray],[0],None,[256],[0,256])
      plt.figure()#新建一個圖像
      plt.title("Grayscale Histogram")
      plt.xlabel("Bins")#X軸標簽
      plt.ylabel("# of Pixels")#Y軸標簽
      plt.plot(hist)
      plt.xlim([0,256])#設置x坐標軸范圍
      plt.show()
      

3. 彩色圖像直方圖繪制：

#彩色圖像直方圖image = cv2.imread("lenna.png")
cv2.imshow("Original",image)
#cv2.waitKey(0)chans = cv2.split(image)    #把圖像維度切割
colors = ("b","g","r")
plt.figure()
plt.title("Flattened Color Histogram")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")for (chan,color) in zip(chans,colors):hist = cv2.calcHist([chan],[0],None,[256],[0,256])plt.plot(hist,color = color)plt.xlim([0,256])
plt.show()

4.實現結果：

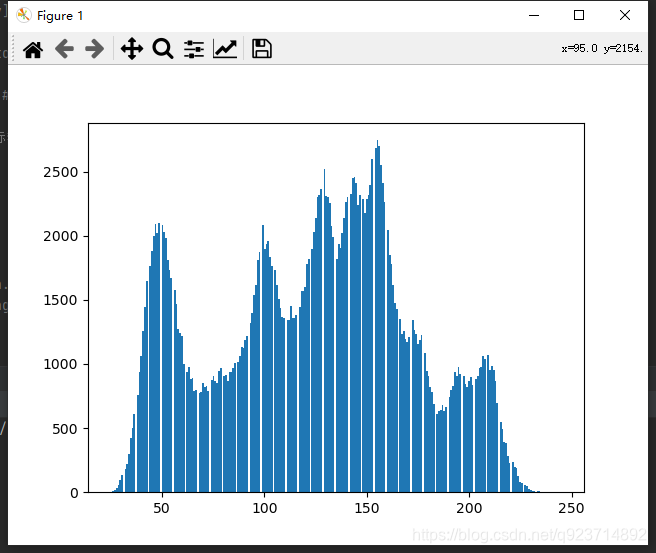
二，直方圖均衡化

1.直方圖均衡化的概念：

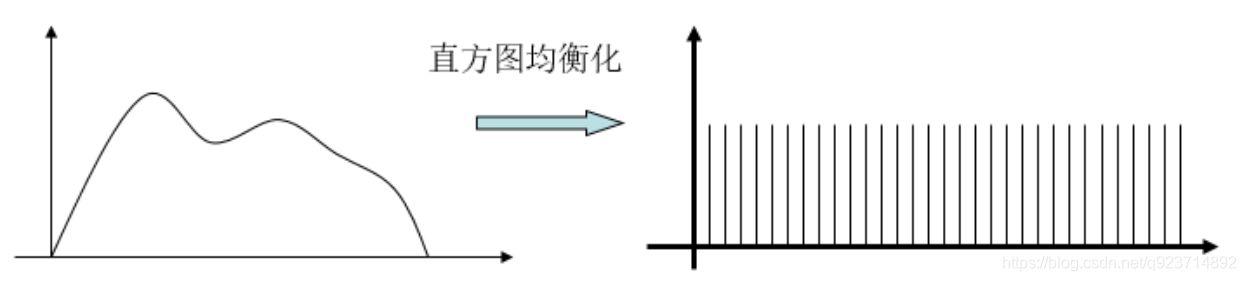
直方圖均衡化是將原圖像的直方圖通過變換函數變為均勻的直方圖，然后按均勻直方圖修改原
圖像，從而獲得一幅灰度分布均勻的新圖像。
直方圖均衡化就是用一定的算法使直方圖大致平和的方法
直方圖均衡化的作用是圖像增強
注意：能適當提升圖像的對比度

2.直方圖均衡化的思想：

為了將原圖像的亮度范圍進行擴展，需要一個映射函數，將原圖像的像素值均衡映射到新直
方圖中，這個映射函數有兩個條件：

1. 為了不打亂原有的順序，映射后亮、暗的大小關系不能改變，
2. 映射后必須在原有的范圍內，比如（0-255）

實現步驟：

1. 依次掃描原始灰度圖像的每一個像素，計算出圖像的灰度直方圖H
2. 計算灰度直方圖的累加直方圖
3. 根據累加直方圖和直方圖均衡化原理得到輸入與輸出之間的映射關系。
4. 最后根據映射關系得到結果：dst(x,y) = H’(src(x,y))進行圖像變換

映射關系的推導：（在實際應用中采用接口調用即可）

1. 對于輸入圖像的任意一個像素p, p∈[0,255], 總能在輸出圖像里有對應的像素q, q∈[0,255] 使得下面等式成立（輸入和輸出的像素總量相等）：
   
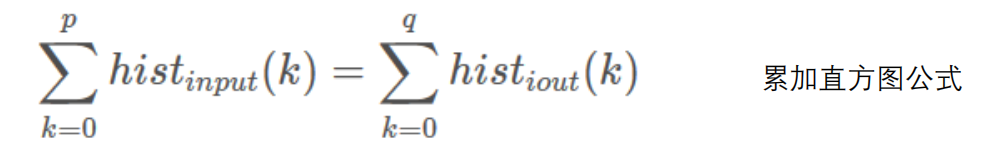
2. 其中，輸出圖像每個灰度級的個數：
   
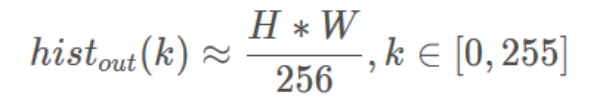
   H和W代表圖像的長和寬，HW就是指圖像中存在的像素點個數*
3. 代入累加直方圖公式：
   
   (q+1)是指從0到q有q+1個值
   最后的結果就是紅色框的公式！
   不過這里要注意：在運算后的q可能是負數，如果要手動實現該算法，這里要處理一下

3.直方圖均衡化的實現舉例：

首先要我們要明確：替換前和替換后的像素值的映射關系如下：

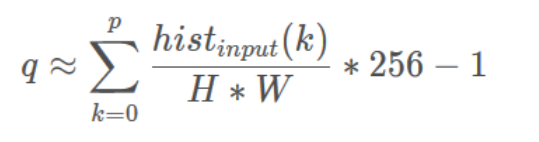
最開始，我們需要均衡化的圖像中的像素值如下：

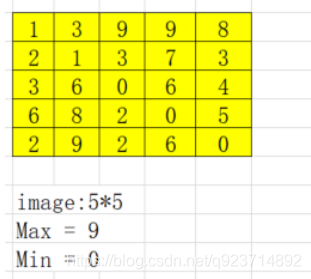
很明顯看出來，這個圖像是5*5的圖像，像素值最高是9，最低是0。
接下來，我們建立一個表格：

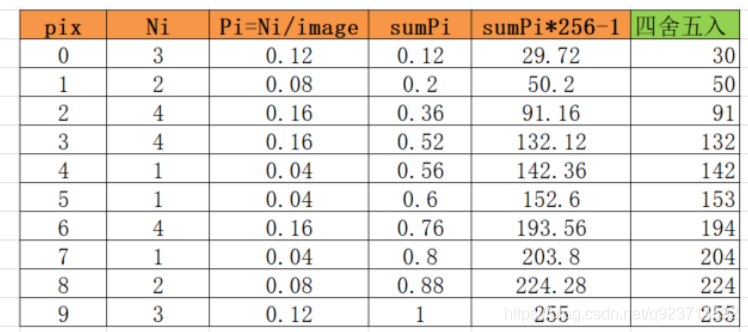
pix值：是指圖像中包含所有的像素值：該圖像是從0-9。
Ni值：是該pix像素值存在的個數，在目標圖像中，0像素有3個，Ni值就為3。
Pi值：是該像素值的概率。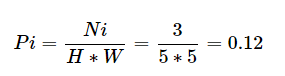
sunmPi值就是之前Pi的總和，也可以看作sumPi=Pi+sumP(i-1)，比如sumP0=P0=0.12，sumP1=sumP0+P1
最后的結果就是sumPi×255-1，最后將這個結果四舍五入后的數值替換原像素數值。

4.代碼實現：

1. 頭文件

import cv2
import numpy as np
from matplotlib import pyplot as plt

2. 灰度圖像直方圖均衡化

'''
equalizeHist—直方圖均衡化
函數原型： equalizeHist(src, dst=None)
src：圖像矩陣(單通道圖像)
dst：默認即可
'''# 獲取灰度圖像
img = cv2.imread("lenna.png", 1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)    #轉換成灰色圖像
#cv2.imshow("image_gray", gray)# 灰度圖像直方圖均衡化
dst = cv2.equalizeHist(gray)# 直方圖
hist = cv2.calcHist([dst],[0],None,[256],[0,256])plt.figure()
plt.hist(dst.ravel(), 256)
plt.show()cv2.imshow("Histogram Equalization", np.hstack([gray, dst]))
cv2.waitKey(0)

3. 彩色圖像直方圖均衡化

# 彩色圖像直方圖均衡化
img = cv2.imread("lenna.png", 1)
cv2.imshow("src", img)# 彩色圖像均衡化,需要分解通道 對每一個通道均衡化
(b, g, r) = cv2.split(img)
bH = cv2.equalizeHist(b)
gH = cv2.equalizeHist(g)
rH = cv2.equalizeHist(r)
# 合并每一個通道
result = cv2.merge((bH, gH, rH))
cv2.imshow("dst_rgb", result)cv2.waitKey(0)

5.實現結果：

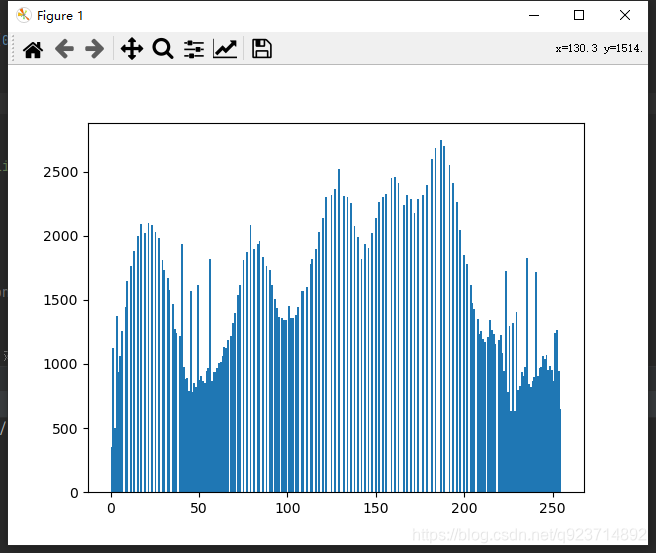
結果對比很明顯發現在直方圖中像素值變的均勻很多，而且明顯均衡化的圖像的對比度更高。