終于到了飯吉圓杯的開賽,這是EZ我參與的歷史上第一場ACM賽制的題目然而沒有罰時
不過題目很好,舉辦地也很成功,為法老點贊!!!
這次和翰爺,吳駿達 dalao,陳樂揚dalao組的隊,因為我們有二個初二的,所以并起來算一個 。
然后我和另外一個初二的連鍵盤都沒摸,靠著翰爺的大殺四方成功A了5題并因為罰時惜敗得到Rank2。%%%Orz 翰爺%%%
好了下面開始講題。飯吉圓鏈接
與一般的ACM相似,這次考試的題目也分為三檔:
- Easy:NOIp普及組+難度(法老認為);NOIp提高組T1,T2難度(我認為)
- Medium:比較套路略加一點思維的NOIp提高組題 (法老認為);NOIpT3+至弱省省選題(我認為)
- Hard: 省選常見算法題,難度略低于省選(法老認為);ZJOI/HNOI省選題+NOI-神題(我認為)
好了我是真的菜,并且針對我無比菜的水平,我也只改了Easy+Medium。
Easy(難度遞增)
I. 「QZEZ第一屆“飯吉圓”杯程序設計競賽」畫展
整場比賽最水的題目了,模擬題不解釋。
由于\(n\le 111\),因此連Hash都不用上。我們直接把圖變成字符串然后開Map存一下即可
CODE
#include<iostream>
#include<cstdio>
#include<map>
#include<string>
using namespace std;
const int N=120;
map <string,bool> t;
int n,m,a,b,ans;
char g[N][N];
bool vis[N][N];
string s;
inline void find(void)
{for (register int i=2;i<=n;++i)if (g[i][2]=='#') { a=i-2; break; }for (register int i=2;i<=m;++i)if (g[2][i]=='#') { b=i-2; break; }
}
inline void solve(int x1,int y1,int x2,int y2)
{register int i,j;for (s="",i=x1;i<=x2;++i)for (j=y1;j<=y2;++j)s+=g[i][j],vis[i][j]=1;if (t[s]) return;for (s="",i=x2;i>=x1;--i)for (j=y2;j>=y1;--j)s+=g[i][j];if (t[s]) return;if (a==b){for (s="",j=y2;j>=y1;--j)for (i=x1;i<=x2;++i)s+=g[i][j];if (t[s]) return;for (s="",j=y1;j<=y2;++j)for (i=x2;i>=x1;--i)s+=g[i][j];if (t[s]) return;}t[s]=1; ++ans;
}
int main()
{//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);register int i,j; ios::sync_with_stdio(false); cin>>n>>m;for (i=1;i<=n;++i)for (j=1;j<=m;++j)cin>>g[i][j]; find();for (i=1;i<=n;++i)for (j=1;j<=m;++j)if (g[i][j]!='#'&&!vis[i][j]) solve(i,j,i+a-1,j+b-1);return printf("%d",ans),0;
}F. 「QZEZ第一屆“飯吉圓”杯程序設計競賽」數學作業
這道題有兩種方法。
第一種當然是暴力證明了,由于我不會,因此給出法老的手寫證明:
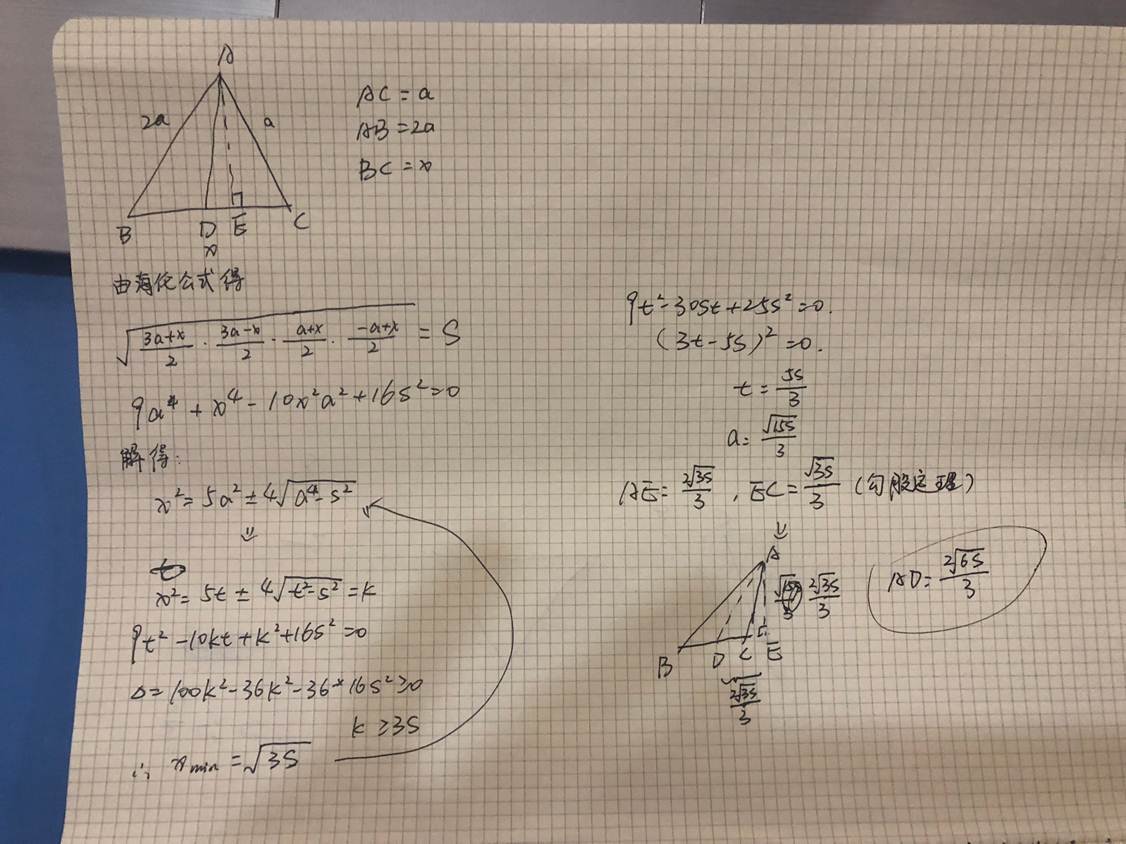
第二種就比較策略了。題目中提到了:
?\(f(s)\)的函數圖像似乎是一個極其詭異的曲線
然后我們根據相似三角形感性理解一下其實面積變大的話其形狀不會改變,只有邊長會按比例增加。
因此我們可以結合樣例得到:
\(f(s)=A \sqrt S=1.63299\sqrt S\)
然后寫上去一交發現WA了!Why?精度!
我們來猥瑣一波:
\((1.63299)^2=2.666...=\frac{8}{3}\)
所以\(A=\frac{2\sqrt S}{3}\)
然后就水過了。
CODE
#include<cstdio>
#include<cmath>
using namespace std;
int main()
{int n; scanf("%d",&n);printf("%.5lf",(double)sqrt(n*8.0/3.0));return 0;
}B. 「QZEZ第一屆“飯吉圓”杯程序設計競賽」最小完美生成樹
也是比較簡單的題目,要正確理解題意
首先我們先對原圖跑一遍MST,如果求出來的MST已經包含多種顏色,那么直接輸出答案即可。
如果只有一種顏色,我們就挑一條不同顏色的邊,然后肯定會有一條邊被替換下來。
我們找到這條邊的最大值即可。
這種方法可以和求LCA一起搞,主要就是倍增。
令\(f_{i,j}\)表示第\(i\)條邊向上\(2^j\)次步的路徑上的最大值,然后和LCA一起做即可(因為剛好也查詢到LCA)
具體維護看CODE
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=100005,P=20;
struct edge
{int to,next,v;
}e[N<<1];
struct data
{int l,r,w,col;bool use;
}a[N];
int head[N],n,m,pa[N][P],f[N][P],father[N],dep[N],cnt,c,rt=1;
long long tot;
inline char tc(void)
{static char fl[100000],*A=fl,*B=fl;return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{x=0; char ch=tc();while (ch<'0'||ch>'9') ch=tc();while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=tc();
}
inline bool comp(data a,data b)
{return a.w<b.w;
}
inline void add(int x,int y,int z)
{e[++cnt].to=y; e[cnt].v=z; e[cnt].next=head[x]; head[x]=cnt;
}
inline int max(int a,int b)
{return a>b?a:b;
}
inline int min(int a,int b)
{return a<b?a:b;
}
inline int getfather(int k)
{return father[k]==k?k:father[k]=getfather(father[k]);
}
inline void DFS(int now,int fa)
{for (register int i=head[now];i!=-1;i=e[i].next)if (e[i].to!=fa) f[e[i].to][0]=e[i].v,pa[e[i].to][0]=now,dep[e[i].to]=dep[now]+1,DFS(e[i].to,now);
}
inline void init(void)
{for (register int j=0;j<P-1;++j)for (register int i=1;i<=n;++i)if (pa[i][j]) pa[i][j+1]=pa[pa[i][j]][j],f[i][j+1]=max(f[i][j],f[pa[i][j]][j]);
}
inline void swap(int &a,int &b)
{int t=a; a=b; b=t;
}
inline int getmax(int x,int y)
{if (dep[x]<dep[y]) swap(x,y); register int i; int res=0;for (i=P-1;i>=0;--i)if (pa[x][i]&&dep[pa[x][i]]>=dep[y]) res=max(res,f[x][i]),x=pa[x][i];if (x==y) return res;for (i=P-1;i>=0;--i)if (pa[x][i]&&pa[y][i]&&pa[x][i]!=pa[y][i]) {res=max(res,max(f[x][i],f[y][i]));x=pa[x][i]; y=pa[y][i];}return max(res,max(f[x][0],f[y][0]));
}
int main()
{//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);register int i; read(n); read(m);memset(e,-1,sizeof(e)); memset(head,-1,sizeof(head));for (i=1;i<=m;++i)read(a[i].l),read(a[i].r),read(a[i].w),read(a[i].col);sort(a+1,a+m+1,comp);for (i=1;i<=n;++i)father[i]=i;for (i=1;i<=m;++i){int fx=getfather(a[i].l),fy=getfather(a[i].r);if (fx!=fy){father[fx]=fy; tot+=a[i].w; a[i].use=1;add(a[i].l,a[i].r,a[i].w); add(a[i].r,a[i].l,a[i].w);}}for (i=1;i<=m;++i)if (a[i].use){if (!c) { c=a[i].col; continue; }if (c!=a[i].col) return printf("%lld",tot),0;}DFS(rt,-1); init(); long long ans=1e18;for (i=1;i<=m;++i)if (!a[i].use&&a[i].col!=c) ans=min(ans,tot-getmax(a[i].l,a[i].r)+a[i].w);return printf("%lld",ans),0;
}Medium(難度遞增)
C. 「QZEZ第一屆“飯吉圓”杯程序設計競賽」路徑計數
比較套路的數位DP。
我們考慮對題意進行轉換,考慮把走過的點寫下來,那么一個點的二進制是另一個點的二進制的子集。
所以每一個路徑上的數肯定是一段1,然后一段0。
就相當于要確定二進制每一位的出現次數,然后出現的二進制位值之和要小于等于\(k\),總和等于\(n\)
仔細想一想,這就是個多重背包了(怎么好像就我一個人寫多重背包)
CODE
#include<cstdio>
#include<cctype>
#include<cstring>
using namespace std;
const int N=1e5+5,mod=1e9+9;
int n,k,f[N],x;
inline void inc(int &x,int y)
{if ((x+=y)>=mod) x-=mod;
}
inline void dec(int &x,int y)
{if ((x-=y)<0) x+=mod;
}
int main()
{register int i,j; scanf("%d%d",&k,&n); f[0]=1;for (i=0;(x=1<<i)<=n;++i){for (j=0;j<=n;++j)if (j>=x) inc(f[j],f[j-x]);for (j=n;j>=0;--j)if (j>=(long long)x*(k+1)) dec(f[j],f[j-(long long)x*(k+1)]);}return printf("%d",f[n]),0;
}K. 「QZEZ第一屆“飯吉圓”杯程序設計競賽」朋友圈
這是典型的技巧題,首先我們想一下這個問題的兩種解決方法:
- 暴力掃描每一條邊,判斷兩端是否在點集內。復雜度為\(O(qm)\)
- 枚舉點集中的兩個點,然后判斷是否存在邊 。復雜度為\(O(q\cdot s\ log\ m)\)
然后這兩種算法的效率取決于每組數據的點數。我們設一個閾值\(S\):
當點數大于\(S\)時進行算法1,否則進行算法2。
然后我們可以得出取\(S=\frac{q}{log\ m}\)時復雜度達到理論最小值\(O(q\cdot\sqrt{m\ log\ m})\)
CODE
#include<cstdio>
#include<cctype>
#include<cmath>
#include<map>
#include<set>
using namespace std;
const int N=200005;
struct edge
{int x,y;
}e[N];
map <int,bool> vis[N];
int n,m,q,blk,t,ans,num[N];
bool s[N];
inline char tc(void)
{static char fl[100000],*A=fl,*B=fl;return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{x=0; char ch; while (!isdigit(ch=tc()));while (x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
}
inline void write(int x)
{if (x>9) write(x/10);putchar(x%10+'0');
}
inline int solve1(void)
{register int i,ans=0;for (i=1;i<=m;++i)if (s[e[i].x]&&s[e[i].y]) ++ans;return ans;
}
inline int solve2(void)
{register int i,j,ans=0;for (i=1;i<t;++i)for (j=i+1;j<=t;++j)if (vis[num[i]][num[j]]) ++ans;return ans;
}
int main()
{//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);register int i; read(n); read(m);for (i=1;i<=m;++i)read(e[i].x),read(e[i].y),vis[e[i].x][e[i].y]=vis[e[i].y][e[i].x]=1; read(q); blk=q/(int)log2(m);while (q--){for (read(t),i=1;i<=t;++i)read(num[i]),s[num[i]]=1;write(t>blk?solve1():solve2()); putchar('\n');for (i=1;i<=t;++i)s[num[i]]=0;}return 0;
}H. 「QZEZ第一屆“飯吉圓”杯程序設計競賽」字符串匹配2
這道題也是有點騷的,就著法老的std寫的,第一次知道雙Hash的正確寫法
首先讀題,我們考慮枚舉所有的周期,然后對于每一段我們可以結合特殊最小表示法+雙Hash來\(O(1)\)求
然后這里我們要知道一個調和級數公式(其實我是知道的,也和另外一個初二口頭AC了這道題,不過最后時間不夠了,而且我們也不敢上):
\(n+\frac{n}{2}+\frac{n}{3}+\frac{n}{4}+\cdots+\frac{n}{n-1}+1=n\ In\ n\)
然后把每種字符出現的位置用01二進制串表示,然后hash,判斷是否能兩兩對應就可以了 。
CODE
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#define fir first
#define sec second
using namespace std;
typedef pair<int,int> Hash;
const int N=1e5+5;
const Hash seed={233,2333},mod={1e9+7,1e9+9};
vector <Hash> a,b;
char s[N];
int len;
Hash pre[5][N],pw[N];
Hash operator %(Hash a,Hash b) { return Hash((a.fir+b.fir)%b.fir,(a.sec+b.sec)%b.sec); }
Hash operator +(Hash a,Hash b) { return Hash(a.fir+b.fir,a.sec+b.sec)%mod; }
Hash operator -(Hash a,Hash b) { return Hash(a.fir-b.fir,a.sec-b.sec)%mod; }
Hash operator *(Hash a,Hash b) { return Hash(1LL*a.fir*b.fir%mod.fir,1LL*a.sec*b.sec%mod.sec); }
inline void write(int x)
{if (x>9) write(x/10);putchar(x%10+'0');
}
inline int min(int a,int b)
{return a<b?a:b;
}
inline Hash get_sub(int k,int l,int r)
{return pre[k][r]-(pre[k][l-1]*pw[r-l+1]);
}
int main()
{register int i,j,k; scanf("%s",s+1); len=strlen(s+1);for (pw[0]={1,1},i=1;i<=len;++i)pw[i]=pw[i-1]*seed;for(i=1;i<=len;++i){for(j=0;j<5;++j) pre[j][i]=pre[j][i-1]*seed;pre[s[i]-'a'][i]=pre[s[i]-'a'][i]+Hash(1,1);}for (i=1;i<=len;++i){bool flag=1;for (j=i+1;j<=len;j+=i){a.clear(); b.clear();for (k=0;k<5;++k)a.push_back(get_sub(k,1,min(i,len-j+1))),b.push_back(get_sub(k,j,min(i+j-1,len)));sort(a.begin(),a.end()); sort(b.begin(),b.end());if (a!=b) { flag=0; break; }}if (flag) write(i),putchar(' ');}return 0;
}E. 「QZEZ第一屆“飯吉圓”杯程序設計競賽」暑假作業
首先先發現對\(t\)從小到大排序后可以得到最優解(這個很好證明而且也很顯然,實在不行結合樣例理解一下即可)。
考慮排序后如何算出初始的最優解,我們可以分析后得出答案等價于:
\(\sum_{i=1}^n l_i-t_i\cdot(n-i+1)\)
然后我們考慮修改,其實就是取走一個數在放上一個數的過程,我們發現只要得出這個點(老的)對答案的貢獻和新的點對答案的貢獻。
很顯然,一個點被刪除/加入對于它的排名有影響,對排在它后面的數的答案也有影響。
因此我們分別考慮這兩個影響,排名可以用類似于求逆序對的方法用樹狀數組求知。
然后考慮對于排在它后面的數統統前移一位,其實也是一個求和(\(\sum t_i\))的過程,因此我們再開一維樹狀數組來直接統計即可。
具體實現看CODE
#include<cstdio>
#include<cctype>
#include<algorithm>
using namespace std;
typedef long long LL;
const LL N=2e5+5;
LL n,m,l[N],t[N],r[N],x,nl,nt,ans,tree[2][N>>1];
inline char tc(void)
{static char fl[100000],*A=fl,*B=fl;return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(LL &x)
{x=0; char ch; while (!isdigit(ch=tc()));while (x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
}
inline void write(LL x)
{if (x<0) putchar('-'),x=-x;if (x>9) write(x/10); putchar(x%10+'0');
}
inline void add(LL x,LL y,LL z)
{for (;x<=1e5;tree[z][x]+=y,x+=x&-x);
}
inline LL get(LL x,LL y)
{LL tot=0; for (;x;tot+=tree[y][x],x-=x&-x); return tot;
}
int main()
{//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);register LL i; read(n); read(m);for (i=1;i<=n;++i)read(l[i]),read(t[i]),r[i]=t[i],ans+=l[i];sort(r+1,r+n+1);for (i=1;i<=n;++i)ans-=r[i]*(n-i+1),add(r[i],1,0),add(r[i],r[i],1);write(ans); putchar('\n');while (m--){read(x); read(nl); read(nt);ans-=l[x]; l[x]=nl; ans+=l[x];add(t[x],-1,0); add(t[x],-t[x],1); ans+=t[x]*(n-get(t[x],0))+get(t[x],1);t[x]=nt; ans-=t[x]*(n-get(t[x],0))+get(t[x],1); add(t[x],1,0); add(t[x],t[x],1);write(ans); putchar('\n');}return 0;
}










)







 的認知)