PCA的概念：

PCA是用來實現特征提取的。
特征提取的主要目的是為了排除信息量小的特征，減少計算量等。
簡單來說：
當數據含有多個特征的時候，選取主要的特征，排除次要特征或者不重要的特征。
比如說：我們要區分貓和狗。那么，貓和狗是否有胡子就變得尤為重要，這屬于主要特征，但是貓和狗的顏色就變得不重要了，這就屬于不重要特征了。但是當我們要區分貓的種類的時候，貓的顏色又變成主要特征了。這說明主要特征是相對的，而不是絕對的。而我們要保留那些對結果更重要的特征，減少不重要的特征，這就是主成分分析。

PCA的實現：

PCA算法是如何實現的？

簡單來說，就是將數據從原始的空間中轉換到新的特征空間中，例如原始的空間是三維的(x,y,z)，x、y、z分別是原始空間的三個基，我們可以通過某種方法，用新的坐標系(a,b,c)來表示原始的數據，那么a、b、c就是新的基，它們組成新的特征空間。在新的特征空間中，可能所有的數據在c上的投影都接近于0，即可以忽略，那么我們就可以直接用(a,b)來表示數據，這樣數據就從三維的(x,y,z)降到了二維的(a,b)。

問題是如何求新的基(a,b,c)?

一般步驟是這樣的：

對原始數據零均值化（中心化），
求協方差矩陣，
對協方差矩陣求特征向量和特征值，這些特征向量組成了新的特征空間。

1.PCA–零均值化（中心化）：

只有中心化數據之后，計算得到的方向才能比較好的“概括”原來的數據。
此圖形象的表述了，中心化的幾何意義，就是將樣本集的中心平移到坐標系的原點O上。
（這一步其實也可以沒有，但是有了更加錦上添花）
在這里插入圖片描述

2.PCA–求協方差矩陣

這里更多是線性代數知識：
協方差就是一種用來度量兩個隨機變量關系的統計量。
同一元素的協方差就表示該元素的方差，不同元素之間的協方差就表示它們的相關性。
協方差：
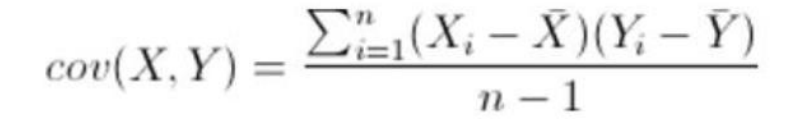
在這里插入圖片描述
方差：

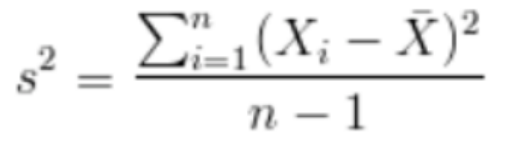
協方差的性質：在這里插入圖片描述
由定義可看出：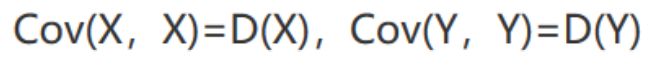
比如，三維(x,y,z)的協方差矩陣：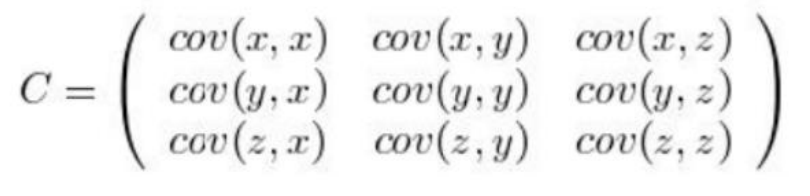

協方差矩陣的特點：
? 協方差矩陣計算的是不同維度之間的協方差，而不是不同樣本之間的。
? 樣本矩陣的每行是一個樣本，每列為一個維度，所以我們要按列計算均值。
? 協方差矩陣的對角線就是各個維度上的方差

特別的，如果做了中心化，則協方差矩陣為（中心化矩陣的協方差矩陣公式）：
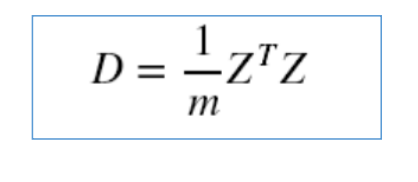
在這里插入圖片描述

3. 對協方差矩陣求特征向量和特征值，這些特征向量組成了新的特征空間。

A為n階矩陣，若數λ和n維非0列向量x滿足Ax=λx，那么數λ稱為A的特征值，x稱為A的對應于特征值λ 的特征向量。式Ax=λx也可寫成( A-λE)x=0，E是單位矩陣，并且|A-λE|叫做A 的特征多項式。當特征多項式等于0的
時候，稱為A的特征方程，特征方程是一個齊次線性方程組，求解特征值的過程其實就是求解特征方
程的解。
對于協方差矩陣A，其特征值（可能有多個）計算方法為：
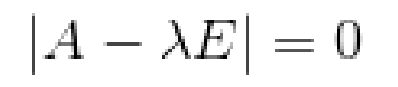
在這里插入圖片描述

（這里就是線性代數知識）
接下來進行排序：特征值越大，意味著相關性越大

PCA–評價模型的好壞，K值的確定

通過特征值的計算我們可以得到主成分所占的百分比，用來衡量模型的好壞。
對于前k個特征值所保留下的信息量計算方法如下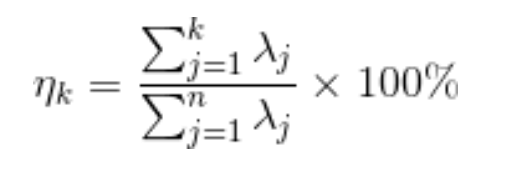：在這里插入圖片描述

PCA–PCA降維的幾何意義：

我們對于一組數據，如果它在某一坐標軸上的方差越大，說明坐標點越分散，該屬性能夠比較
好的反映源數據。所以在進行降維的時候，主要目的是找到一個超平面，它能使得數據點的分
布方差呈最大，這樣數據表現在新的坐標軸上時候已經足夠分散了。
PCA算法的優化目標就是:
① 降維后同一維度的方差最大
② 不同維度之間的相關性為0

PCA算法的優缺點：

優點：

完全無參數限制的。在PCA的計算過程中完全不需要人為的設定參數或是根據任何經驗模型對計
算進行干預，最后的結果只與數據相關，與用戶是獨立的。
用PCA技術可以對數據進行降維，同時對新求出的“主元”向量的重要性進行排序，根據需要取前
面最重要的部分，將后面的維數省去，可以達到降維從而簡化模型或是對數據進行壓縮的效果。同
時最大程度的保持了原有數據的信息。
各主成分之間正交，可消除原始數據成分間的相互影響。
計算方法簡單，易于在計算機上實現。

缺點：

如果用戶對觀測對象有一定的先驗知識，掌握了數據的一些特征，卻無法通過參數化等方法對處
理過程進行干預，可能會得不到預期的效果，效率也不高。
貢獻率小的主成分往往可能含有對樣本差異的重要信息。

PCA的代碼實現：

PCA接口實現：

import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]])  #導入數據，維度為4
pca = PCA(n_components=2)   #降到2維
pca.fit(X)                  #訓練
newX=pca.fit_transform(X)   #降維后的數據
# PCA(copy=True, n_components=2, whiten=False)
print(pca.explained_variance_ratio_)  #輸出貢獻率
print(newX)                  #輸出降維后的數據

PCA函數實現：

import numpy as np
class PCA():def __init__(self,n_components):self.n_components = n_componentsdef fit_transform(self,X):self.n_features_ = X.shape[1]# 求協方差矩陣X = X - X.mean(axis=0)self.covariance = np.dot(X.T,X)/X.shape[0]# 求協方差矩陣的特征值和特征向量eig_vals,eig_vectors = np.linalg.eig(self.covariance)# 獲得降序排列特征值的序號idx = np.argsort(-eig_vals)# 降維矩陣self.components_ = eig_vectors[:,idx[:self.n_components]]# 對X進行降維return np.dot(X,self.components_)# 調用
pca = PCA(n_components=2)
X = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]])  #導入數據，維度為4
newX=pca.fit_transform(X)
print(newX)                  #輸出降維后的數據

PCA手動函數實現：

"""
使用PCA求樣本矩陣X的K階降維矩陣Z
"""import numpy as npclass CPCA(object):'''用PCA求樣本矩陣X的K階降維矩陣ZNote:請保證輸入的樣本矩陣X shape=(m, n)，m行樣例，n個特征'''def __init__(self, X, K):''':param X,訓練樣本矩陣X:param K,X的降維矩陣的階數，即X要特征降維成k階'''self.X = X       #樣本矩陣Xself.K = K       #K階降維矩陣的K值self.centrX = [] #矩陣X的中心化self.C = []      #樣本集的協方差矩陣Cself.U = []      #樣本矩陣X的降維轉換矩陣self.Z = []      #樣本矩陣X的降維矩陣Zself.centrX = self._centralized()self.C = self._cov()self.U = self._U()self.Z = self._Z() #Z=XU求得def _centralized(self):'''矩陣X的中心化'''print('樣本矩陣X:\n', self.X)centrX = []mean = np.array([np.mean(attr) for attr in self.X.T]) #樣本集的特征均值print('樣本集的特征均值:\n',mean)centrX = self.X - mean ##樣本集的中心化print('樣本矩陣X的中心化centrX:\n', centrX)return centrXdef _cov(self):'''求樣本矩陣X的協方差矩陣C'''#樣本集的樣例總數ns = np.shape(self.centrX)[0]#樣本矩陣的協方差矩陣CC = np.dot(self.centrX.T, self.centrX)/(ns - 1)print('樣本矩陣X的協方差矩陣C:\n', C)return Cdef _U(self):'''求X的降維轉換矩陣U, shape=(n,k), n是X的特征維度總數，k是降維矩陣的特征維度'''#先求X的協方差矩陣C的特征值和特征向量a,b = np.linalg.eig(self.C) #特征值賦值給a，對應特征向量賦值給b。函數doc：https://docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.eig.html print('樣本集的協方差矩陣C的特征值:\n', a)print('樣本集的協方差矩陣C的特征向量:\n', b)#給出特征值降序的topK的索引序列ind = np.argsort(-1*a)#構建K階降維的降維轉換矩陣UUT = [b[:,ind[i]] for i in range(self.K)]U = np.transpose(UT)print('%d階降維轉換矩陣U:\n'%self.K, U)return Udef _Z(self):'''按照Z=XU求降維矩陣Z, shape=(m,k), n是樣本總數，k是降維矩陣中特征維度總數'''Z = np.dot(self.X, self.U)print('X shape:', np.shape(self.X))print('U shape:', np.shape(self.U))print('Z shape:', np.shape(Z))print('樣本矩陣X的降維矩陣Z:\n', Z)return Zif __name__=='__main__':'10樣本3特征的樣本集, 行為樣例，列為特征維度'X = np.array([[10, 15, 29],[15, 46, 13],[23, 21, 30],[11, 9,  35],[42, 45, 11],[9,  48, 5],[11, 21, 14],[8,  5,  15],[11, 12, 21],[21, 20, 25]])K = np.shape(X)[1] - 1print('樣本集(10行3列，10個樣例，每個樣例3個特征):\n', X)pca = CPCA(X,K)

PCA應用——鳶尾花數據集

import matplotlib.pyplot as plt
import sklearn.decomposition as dp
from sklearn.datasets.base import load_irisx,y=load_iris(return_X_y=True) #加載數據，x表示數據集中的屬性數據，y表示數據標簽
pca=dp.PCA(n_components=2) #加載pca算法，設置降維后主成分數目為2
reduced_x=pca.fit_transform(x) #對原始數據進行降維，保存在reduced_x中
red_x,red_y=[],[]
blue_x,blue_y=[],[]
green_x,green_y=[],[]
for i in range(len(reduced_x)): #按鳶尾花的類別將降維后的數據點保存在不同的表中if y[i]==0:red_x.append(reduced_x[i][0])red_y.append(reduced_x[i][1])elif y[i]==1:blue_x.append(reduced_x[i][0])blue_y.append(reduced_x[i][1])else:green_x.append(reduced_x[i][0])green_y.append(reduced_x[i][1])
plt.scatter(red_x,red_y,c='r',marker='x')
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()

PCA的一點思考：

正如開頭我舉的例子，當區分貓狗之間時，PCA將胡子等關鍵信息作為主要特征，但是當區分貓的種類時，PCA是如何做到在貓中把顏色也作為主要特征？就是說從隨著算法目標的改變，如何做到主要特征的改變？
我后來想了想，我覺得PCA是針對數據集中各數據互相之間的差距。當分析貓狗時，數據集中主要是貓和狗，當對數據集中進行PCA時，針對的是方差較大的一些數據特征，但是當分析貓的種類時，數據集中主要是貓，方差較大的數據特征就變成了顏色等主要特征。