1 單選題(每題 2 分,共 30 分)
第1題 下列哪一項不是面向對象編程(OOP)的基本特征?(?? )
A. 繼承 (Inheritance)???? ??????????????????????????????????????????? B. 封裝 (Encapsulation)
C. 多態 (Polymorphism)?????????????????????????????????????????? D. 鏈接 (Linking)
解析:答案D。?面向對象編程的基本特征包含封裝、繼承、多態和抽象四大核心要素?,這四大特征共同構成了代碼組織的核心范式,有效提升了程序的可維護性、擴展性和復用性。????所以D.不是。故選D。
第2題 為了讓 Dog 類的構造函數能正確地調用其父類 Animal 的構造方法,橫線線處應填入(?? )。
- class Animal:
- ????def __init__(self, name: str):
- ????????self.name = name
- ????????print("Animal created")
- ????def speak(self) -> None:
- ????????print("Animal speaks")
- class Dog(Animal):
- ????______________________________
- ????????print("Dog created")
- ????def speak(self) -> None:
- ????????print("Dog barks")
- if __name__ == "__main__":
- ????animal: Animal = Dog("Rex", "Labrador")
- ????animal.speak()
A. |
|
B. |
|
C. |
|
D. |
|
解析:答案A。?繼承父類構造函數?:子類?Dog?需要通過?super().__init__(name)?顯式調用父類?Animal?的構造函數,以確保執行父類構造函數(如?self.name = name?和打印?"Animal created")被執行。?擴展子類屬性?:Dog?類新增了?breed?屬性,需要在子類構造函數中初始化?self.breed = breed。所以A.的代碼完全符合上述邏輯,而其他選項(B.、C.、D.)要么遺漏了?super().__init__(),要么語法不完整。故選A。
第3題 代碼同上一題,代碼animal.speak()執行后輸出結果是(?? )。
A. 輸出 Animal speaks? ? ? B. 輸出 Dog barks? ? ? ? ?C. 編譯錯誤????????????? ? ? ? ? ? ?D. 程序崩潰
解析:答案?B?。?Dog?實例化時,通過?super().__init__("Rex")?調用父類?Animal?的構造函數,執行?print("Animal created")?并初始化?name?屬性。Dog?的構造函數繼續執行?print("Dog created")。最后調用?animal.speak(),由于?Dog?重寫了?speak?方法,輸出?"Dog barks"?,所以輸出?Dog barks。故選B。
第4題 以下Python代碼執行后其輸出是(?? )。
- from collections import deque
- stack = []
- queue = deque()
- # 元素入棧/入隊(1, 2, 3)
- for i in range(1, 4):
- ????stack.append(i)
- ????queue.append(i)
- print(f"{stack[-1]} {queue[0]}")
A. 1 3??????????????????? ? ? ? ? ? ? ? ?B. 3 1????????????? ? ? ? ? ? ? ? ? ? C. 3 3???????????? ? ? ? ? ? ? ? ? ? ? ? ?D. 1 1
?解析:答案?B?。棧和隊列的操作?:棧(stack)是先進后出(FILO)結構,本題用列表模擬,append(i)?依次添加?1, 2, 3,因此?stack[-1](棧頂元素,列表最后的元素)為?3。隊列(deque)是先進先出(FIFO)結構, append(i)?依次添加?1, 2, 3,因此?queue[0](隊首元素)為?1。所以?輸出結果?為f"{stack[-1]} {queue[0]}"的結果為?"3 1"。故選B。
第5題 在一個使用列表實現的循環隊列中,front 表示隊頭元素的位置(索引),rear 表示隊尾元素的下一個插入位置(索引),隊列的最大容量為 maxSize。那么判斷隊列已滿的條件是(?? )
A. rear == front????????????????? ????????????????????????????????????????B. (rear + 1) % maxSize == front
C. (rear - 1 + maxSize) % maxSize == front?????????????D. (rear - 1) == front
解析:答案?B?。在?循環隊列?中,判斷隊列已滿的條件需要滿足以下兩點:?隊尾指針(rear)的下一個位置是隊頭指針(front)?,即?rear?即將追上?front。?為了避免rear == front時出現歧義?(此時隊列可能為空也可能為滿),通常使用?(rear + 1) % maxSize == front?來判斷是否已滿。rear == front?用于判斷?空隊列,所以A.錯誤。(rear - 1 + maxSize) % maxSize == front?:
等價于?rear - 1 == front,C.、D.相同,所以兩者都錯。故選B。
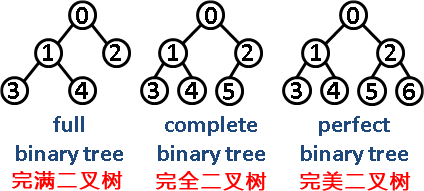
第6題 在二叉樹中,只有最底層的節點未被填滿,且最底層節點盡量靠左填充的是(?? )。
A. 完美二叉樹? ? ? ? ? ? ? ? B. 完全二叉樹? ? ? ? ? ? ? ? C. 完滿二叉樹? ? ? ? ? ? ? ? D. 平衡二叉樹
解析:答案?B?。?完美二叉樹(Perfect Binary Tree):一個深度為k(>=1)且有2^(k-1) - 1個結點的二叉樹稱為完美二叉樹。(注:國內的數據結構教材大多翻譯為"滿二叉樹")。完全二叉樹(Complete Binary Tree):完全二叉樹從根結點到倒數第二層滿足完美二叉樹,最后一層可以不完全填充,其葉子結點都靠左對齊。完滿二叉樹(Full Binary Tree):所有非葉子結點的度都是2。(只要你有孩子,你就必然是有兩個孩子。)所以B.正確。故選B。
第7題 在使用數組(列表)表示完全二叉樹時,如果一個節點的索引為𝑖(從0開始計數),那么其左子節點的索引通常是(?? )。
A.(i-1)/2? ? ? ? ? ? ? ? ??? ? ? ? ? ? ?B.i+1? ? ? ? ? ? ?? ? ? ? ? ? ? ? ?C.i+2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?D.2*i+1
解析:答案D?。在使用數組表示完全二叉樹時,節點的索引從?0開始?,其子節點的索引計算規則為:?左子節點?的索引為2*i + 1,?右子節點?的索引為2*i + 2。例如:根節點?i = 2:左子節點?i = 2*2 + 1 = 5,右子節點?i = 2*2 + 2 = 6,D.?正確。故選D。
第8題 已知一棵二叉樹的前序遍歷序列為GDAFEMHZ,中序遍歷序列為ADFGEHMZ,則其后序遍歷序列為(?? )。
A. ADFGEHMZ? ? ? ? ? ? ?B. ADFGHMEZ? ? ? ? ? ? ?C. AFDGEMZH? ? ? ? ? ? ?D. AFDHZMEG
解析:答案D?。由前序遍歷序列可知根節點為G,由中序遍歷序列可知左樹為AFD,右樹為EHMZ,后序遍歷序列左樹、右樹、根節點,只有D.的結構符合。具體:前序遍歷?(根-左-右)的第一個元素?G?是?根節點?。?中序遍歷?(左-根-右)中,G?左側?ADF?是?左子樹?,右側?EMHZ?是?右子樹?。?前序遍歷左子樹?DAF?,中序遍歷左樹?ADF,D子樹根,左節點A,右節點F。前序遍歷右子樹?EMHZ,中序遍歷右子樹EHMZ,E為子樹根,只有右子樹。前序遍歷E右子樹MHZ,中序遍歷E右子樹HMZ,M為子樹根,左節點為H,右節點為Z。構成二叉樹為:
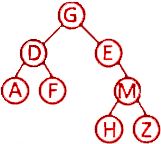
?所以后序遍歷序列為AFDHZMEG,D.?正確。故選D。
第9題 設有字符集 {a, b, c, d, e},其出現頻率分別為 {5, 8, 12, 15, 20},得到的哈夫曼編碼為(?? )。
A. |
| B. |
| C. |
| D. |
|
解析:答案A。哈夫曼編碼的特點,頻率低的用長編碼,頻率高的用短編碼。a最低,b次之,d次高,e最高,e短編碼、a長編碼,d短編碼,b長編碼,只有A.符合。具體:a合并b為13,c合并13(ab)為25,d合并e為35,25合并35為60。
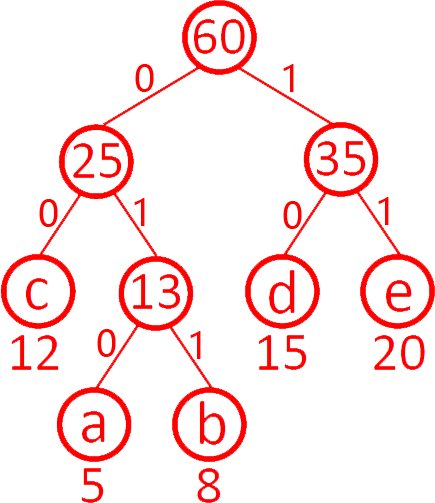
A.?正確。故選A。
第10題 3位格雷編碼中,編碼101之后的下一個編碼是(?? )。
A. 100???????????????????????? ? ? ? ? ?B. 111?????????????????? ? ? ? ? ? ?C. 110????????? ? ? ? ? ? ? ? ? ? ? ? ? D. 001
解析:答案C?。格力雷編碼中,相鄰兩處碼只有一位變化。編碼?101?在標準序列中的下一個編碼應為?100(僅最低位變化),次序與高位為0的次序相反,A.正確。111是110?的下一個編碼,非?101?的相鄰碼。110?和?001?與?101?的漢明距離大于1,不符合格雷碼規則。故選A。
第11題 請將下列Python實現的深度優先搜索(DFS)代碼補充完整,橫線處應填入(?? )。
- from typing import List, Optional
- class TreeNode:
- ????def __init__(self, val=0, left=None, right=None):
- ????????self.val = val
- ????????self.left = left
- ????????self.right = right
- def dfs_preorder(root: Optional[TreeNode], result: List[int]) -> None:
- ????if root is None:
- ????????return
- ????_____________________________
A. |
|
B. |
|
C. |
|
D. |
|
解析:答案A?。題目要求補充一個深度優先搜索(DFS)的代碼片段,二叉樹的深度優先分為:先序遍歷、中序遍歷、后序遍歷。觀察選項可以發現,除D.外result.append()都在第1行,屬前序遍歷,屬前序遍歷順序是:?根節點 → 左子樹 → 右子樹?,因此應?result.append(root.val),再遞歸遍歷左、右子樹,所以A.正確。B.缺少右子樹的遍歷,C.缺少左子樹的遍歷,D.沒有訪問根節點,所以B.、C.、D.錯誤。故選A。
第 12 題 給定一個二叉樹,返回每一層中最大的節點值,結果以數組形式返回,橫線處應填入(?? )。
- from collections import deque
- import math
- from typing import List, Optional
- class TreeNode:
- ????def __init__(self, val=0, left=None, right=None):
- ????????self.val = val
- ????????self.left = left
- ????????self.right = right
- def largestValues(root: Optional[TreeNode]) -> List[int]:
- ????result = []
- ????if not root:
- ????????return result
- ????queue = deque([root])
- ????while queue:
- ????????level_size = len(queue)
- ????????max_val = -math.inf
- ????????for _ in range(level_size):
- ????????????________________________
- ????????????if node.left:
- ????????????????queue.append(node.left)
- ????????????if node.right:
- ????????????????queue.append(node.right)
- ????????result.append(max_val)
- ????return result
A. |
| B. |
|
C. |
| D. |
|
解析:答案D。題目要求實現?按層遍歷二叉樹并返回每層最大值?,使用?廣度優先搜索(BFS)?,編程使用隊列。使用隊列?deque?逐層處理節點。每層開始時,用?level_size?記錄當前層節點數,遍歷當前層所有節點,記錄最大值?max_val。queue.popleft()?是BFS的標準操作(先進先出),確保按層順序處理節點,max_val = max(max_val, node.val)?動態更新當前層的最大值,所以D.正確。popright()?不是?deque?的有效方法,且邏輯錯誤,所以A.錯誤。?B.缺少更新?max_val?的步驟,無法記錄最大值、?C.缺少?node = queue.popleft(),無法獲取節點值進行比較,所以B.、C.錯誤。故選D。
第13題 下面代碼實現一個二叉排序樹的插入函數(沒有相同的數值),橫線處應填入(?? )。
- class TreeNode:
- ????def __init__(self, val=0, left=None, right=None):
- ????????self.val = val
- ????????self.left = left
- ????????self.right = right
- def insert(root, key):
- ????if root is None:
- ????????return TreeNode(key)
- ????___________________________
- ????return root
A. |
|
B. |
|
C. |
|
D. |
|
解析:答案A?。題目要求實現二叉排序樹(BST)的插入操作,且不允許重復值。BST的插入規則是:(1)如果當前節點為null,創建新節點。(2)如果?key??小于?當前節點值,遞歸插入?左子樹?。(3)如果?key??大于?當前節點值,遞歸插入?右子樹?。因不允許重復值,所以相等不處理。??A?.正確實現BST插入邏輯(左小右大),所以正確。?B?.左小,但否則條件永不成立,所以錯誤。C. elif key >= root.val?會導致重復值(題目不允許)且全部插入到左子樹,所以錯誤。?D?. 左右子樹插入邏輯完全顛倒(左子樹插入右子樹,右子樹插入左子樹),所以錯誤。故選A。
第14題 以下關于動態規劃算法特性的描述,正確的是(?? )。
A. 子問題相互獨立,不重疊????????????????????????????????? B. 問題包含重疊子問題和最優子結構
C. 只能從底至頂迭代求解??????????????????????????????????? ? D. 必須使用遞歸實現,不能使用迭代
解析:答案B?。動態規劃(Dynamic Programming, DP)的核心特性包括:1)?重疊子問題?:問題可以被分解為重復出現的子問題,通過記憶化或表存儲避免重復計算;2)?最優子結構?:問題的最優解包含其子問題的最優解,從而能夠遞推求解。??B?. 問題包含重疊子問題和最優子結構,正確。?A.動態規劃的子問題通常是重疊的(否則可直接用分治法解決)?,錯誤。?C.動態規劃可以從頂至底(遞歸+記憶化)或底至頂(迭代)兩種方式求解,?錯誤。?D.動態規劃的實現既支持遞歸,也支持迭代,?錯誤。故選B。
第15題 給定𝑛個物品和一個最大承重為𝑊的背包,每個物品有一個重量𝑤𝑡[𝑖]和價值𝑣𝑎𝑙[𝑖],每個物品只能選擇放或不放。目標是選擇若干個物品放入背包,使得總價值最大,且總重量不超過𝑊。關于下面代碼,說法正確的是(?? )。
- def knapsack1D(W: int, wt: list[int], val: list[int], n: int) -> int:
- ????dp = [0] * (W + 1)
- ????for i in range(n):
- ????????for w in range(W, wt[i] - 1, -1):
- ????????????dp[w] = max(dp[w], dp[w - wt[i]] + val[i])
- ????return dp[W]
A. 該算法不能處理背包容量為 0 的情況
B. 外層循環 i 遍歷背包容量,內層遍歷物品
C. 從大到小遍歷 w 是為了避免重復使用同一物品
D. 這段代碼計算的是最小重量而非最大價值
正確答案:?C. 從大到小遍歷 w 是為了避免重復使用同一物品?
解析:答案C。本題代碼實現的是?0/1背包問題?的經典動態規劃解法,使用一維數組?dp[w]?表示容量為?w?時的最大價值。外層循環遍歷物品(i),內層循環從大到小遍歷背包容量(w),目的是確保每個物品?僅被使用一次?。當?W=0?時,dp[0]?初始化為 0,直接返回 0,能正確處理,所以A.錯誤。外層循環遍歷物品(i),內層循環遍歷背包容量(w),B.反了,所以錯誤。從大到小遍歷?w?是為了避免覆蓋?dp[w - wt[i]],從而防止同一物品被重復使用,C.正確。代碼明確計算的是最大價值(max(dp[w], dp[w - wt[i]] + val[i])),D.錯誤。故選C。
?
2 判斷題(每題 2 分,共 20 分)
第1題 構造函數只能自動不可以被手動調用。(?? )
解析:答案錯誤。Python的構造函數(__init__)?可以通過特定方式手動調用?。故錯誤。
第2題 給定一組字符及其出現的頻率,構造出的哈夫曼樹是唯一的。(?? )
解析:答案錯誤。當存在多個相同權值的節點時,合并順序不同會導致不同的樹形結構。例如,頻率集合{2,2,3,3},因同頻次序調整,可能生成多種不同形態的哈夫曼樹,但他們的帶權路徑長度(WPL)是相同的。故錯誤。
第3題 為了實現一個隊列,使其出隊操作( pop )的時間復雜度為O(1)并且避免數組刪除首元素的O(n)問題,一種常見且有效的方法是使用環形數組,通過調整隊首和隊尾指針來實現。(?? )
解析:答案正確。題目描述的實現隊列的方式是?環形數組(列表)組成循環隊列?,其核心思路確實是通過調整?隊首(front)和隊尾(rear)指針?來高效進行出入隊操作,避免移動數組元素的開銷。?環形數組的?:當隊尾指針到達數組末尾時,可以繞回到數組開頭(環形結構),避免頻繁擴容或移動元素。?入隊(push)?:rear = (rear + 1) % capacity(O(1));?出隊(pop)?:front = (front + 1) % capacity(O(1))。傳統數組隊列刪除首元素需要移動后續所有元素(O(n)),而環形隊列僅需移動指針(O(1))。故正確。
第4題 對一棵從小到大的二叉排序樹進行中序遍歷,可以得到一個遞增的有序序列。(?? )
解析:答案正確。二叉排序樹的定義?:
左子樹的所有節點值 ?小于? 當前節點值。右子樹的所有節點值 ?大于? 當前節點值。
?中序遍歷(左-根-右)的特性?:先遍歷左子樹(所有值更小),再訪問根節點,最后遍歷右子樹(所有值更大)。因此,中序遍歷結果必然按?升序排列。故正確。
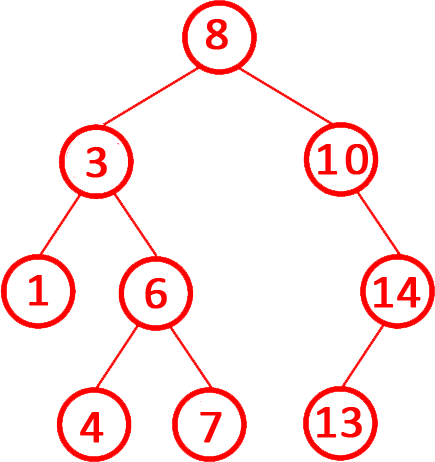
第5題 如果二叉搜索樹在連續的插入和刪除操作后,所有節點都偏向一側,導致其退化為類似于鏈表的結構,這時 其查找、插入、刪除操作的時間復雜度會從理想情況下的O(log n)退化到O(n log n)。(?? )
解析:答案錯誤。二叉搜索樹(BST)又稱二叉查找樹或二叉排序樹。題目考察?二叉搜索樹(BST)退化后的時間復雜度?,判斷其查找、插入、刪除操作是否會從?O(log n)?退化為?O(n log n)。理想情況(平衡BST)?查找、插入、刪除的時間復雜度為O(log n)。?退化情況(退化為鏈表)?:樹高度變為n,操作需遍歷所有節點,時間復雜度退化為?O(n)。
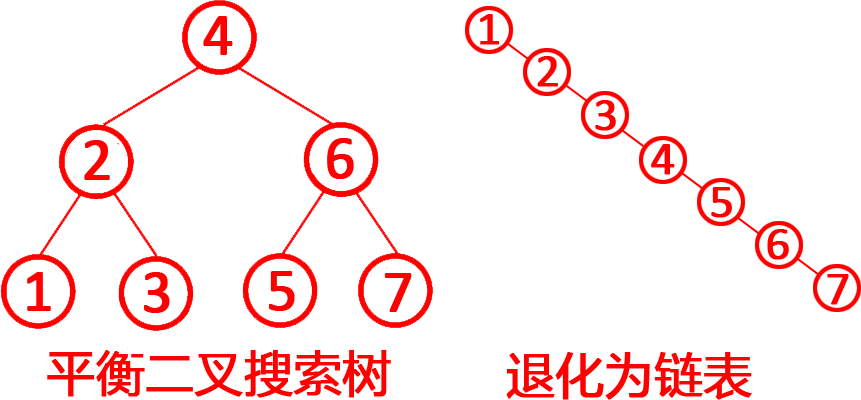
?退化原因?:若插入或刪除的序列有序(如連續遞增或遞減),BST會退化為單側鏈表,樹高度從?log n?變為?n。如上圖所示。?查找?:需遍歷整條“鏈”,時間復雜度?O(n)。?插入/刪除?:同樣需遍歷到末端或目標位置,時間復雜度O(n),而不是O(n log n),所以錯誤。
第6題 執行下列代碼, my_dog.name 的最終值是 Charlie 。(?? )
- class Dog:
- ????def __init__(self, name):
- ????????self.name = name
- if __name__ == "__main__":
- ????my_dog = Dog("Buddy")
- ????my_dog.name = "Charlie"
解析:答案正確。?構造函數初始化?(第2行):def __init__(self, name):為傳入的name字符串。第6行用Dog類建my_dog對象my_dog=Dog("Buddy")?會調用構造函數,將?name?初始化為?"Buddy"。第7行給對象成員賦值,?修改成員變量,my_dog.name = "Charlie" 顯式修改name的值為"Charlie",my_dog.name?的最終值為?"Charlie",所以正確。
第7題 下列 python 代碼可以成功執行,并且子類 Child 的實例能通過其成員函數訪問父類 Parent 的屬性 _value 。(?? )
- class Parent:
- ????def __init__(self):
- ????????self._value = 100
- class Child(Parent):
- ????def get_protected_val(self):
- ????????return self._value
?解析:答案:正確?。Child?繼承自?Parent,因此?Child?的實例會調用?Parent.__init__()?并初始化?self._value(值為100)。_value?是單下劃線前綴的“受保護”屬性(約定俗成,非語法強制),子類可通過?self._value?直接訪問。get_protected_val()?方法返回?self._value,邏輯正確。故正確。
第8題 下列代碼中的 tree 列表,表示的是一棵完全二叉樹 ( -1 代表空節點)按照層序遍歷的結果。(?? )
- tree = [1, 2, 3, 4, -1, 6, 7]
解析:答案?錯誤?。?完全二叉樹的定義?:除最后一層外,其他層節點必須?完全填充?(無空缺)。最后一層節點?從左到右連續排列?(不能有中間空缺)。層序遍歷結果:[1, 2, 3, 4, -1, 6, 7](-1 表示空節點)。
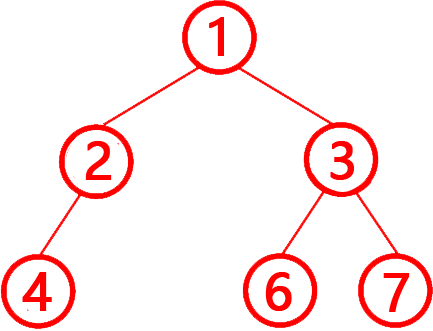
?第3層(節點索引4)?:值為 -1(空節點,參考上圖),但后續仍有 6 和 7 節點。?違反完全二叉樹?“最后一層節點?從左到右連續排列?(不能有中間空缺)”的規則,該樹不是完全二叉樹,所以錯誤。
第9題 在樹的深度優先搜索(DFS)中,可以使用棧作為輔助數據結構以實現“先進后出”的訪問順序。(?? )
解析:答案??正確?。樹的深度優先搜索(DFS)確實使用?棧?作為輔助數據結構,其“先進后出”(FILO)特性確保優先深入探索分支,符合DFS的核心邏輯。故正確。
第10題 下面代碼采用動態規劃求解零錢兌換問題:給定 𝑛 種硬幣,第 𝑖 種硬幣的面值為 𝑐𝑜𝑖𝑛𝑠[𝑖 ? 1] ,目標金額為 𝑎𝑚𝑡 ,每種硬幣可以重復選取,求能夠湊出目標金額的最少硬幣數量;如果不能湊出目標金額,返回 -1 。(?? )
- def coinChangeDPComp(coins: list[int], amt: int) -> int:
- ????n = len(coins)
- ????MAX = amt + 1
- ????dp = [MAX] * (amt + 1)
- ????dp[0] = 0
- ????for i in range(1, n + 1):
- ????????for a in range(1, amt + 1):
- ????????????if coins[i - 1] > a:
- ????????????????dp[a] = dp[a]
- ????????????else:
- ????????????????dp[a] = min(dp[a], dp[a - coins[i - 1]] + 1)
- ????return dp[amt] if dp[amt] != MAX else -1
?解析:答案??正確?。?動態規劃狀態定義?:dp[a]表示湊出金額a所需的最少硬幣數,初始化時設為MAX不可達狀態)。dp[0] = 0是邊界條件,表示金額為0時不需要硬幣。?狀態轉移方程?:對于每種硬幣coins[i-1],若其面值小于等于當前金額a,則更新dp[a]為min(dp[a], dp[a - coins[i-1]] + 1)。若硬幣面值大于 a,則保持dp[a]不變(代碼第12-16行)。?遍歷順序?:外層循環遍歷硬幣種類(i),內層循環遍歷金額(a),確保每種硬幣可重復使用(完全背包問題)。若 dp[amt] 未被更新(仍為 MAX),說明無法湊出目標金額,返回 -1;否則返回 dp[amt]。所以代碼邏輯正確,符合動態規劃解決零錢兌換問題的標準實現。故正確。
3 編程題(每題 25 分,共 50 分)
3.1 編程題1
- 試題名稱:學習小組
- 時間限制:3.0 s
- 內存限制:512.0 MB
3.1.1 題目描述
班主任計劃將班級里的𝑛名同學劃分為若干個學習小組,每名同學都需要分入某一個學習小組中。觀察發現,如果一個學習小組中恰好包含𝑘名同學,則該學習小組的討論積極度為a?。
給定討論積極度a?, a?,...,a?,請你計算將這𝑛名同學劃分為學習小組的所有可能方案中,討論積極度之和的最大值。
3.1.2 輸入格式
第一行,一個正整數𝑛,表示班級人數。
第二行,𝑛個非負整數a?, a?,...,a?,表示不同人數學習小組的討論積極度。
3.1.3 輸出格式
輸出共一行,一個整數,表示所有劃分方案中,學習小組討論積極度之和的最大值。
3.1.4 樣例
3.1.4.1 輸入樣例1
- 4
- 1 5 6 3
3.1.4.2 輸出樣例1
- 10
3.1.4.3 輸入樣例2
- 8
- 0 2 5 6 4 3 3 4
3.1.4.4 輸出樣例2
- 12
3.1.5 數據范圍
對于40%的測試點,保證1≤𝑛≤10。
對于所有測試點,保證1≤𝑛≤1000,0≤a?≤10?。
3.1.6 編寫程序思路
分析:題目是分組優化問題:給定?n?名同學和一組討論討論積極度a??,a??,...,a??(其中a?表示一個小組恰好有k名同學時的討論積極度),目標是將所有同學劃分為若干個學習小組(每個小組至少包含 1 名同學),使得所有小組的討論討論積極度之和最大。每個同學必須被分配到恰好一個小組中,小組大小k可以是1到n之間的任意整數,且小組大小k對應的討論積極度a??由輸入給出(非負整數)。?目標函數?:最大化所有小組的討論積極度之和。?該問題可以建模為一個完全背包問題:"物品" 對應于小組大小k(k=1,2,...,n),每種物品可以無限次使用(即可以創建多個相同大小的小組);"物品重量" 為小組大小k;"物品價值" 為討論積極度a??。"背包容量" 為總人數n,要求恰好裝滿背包(所有同學都被分配)。可以使用動態規劃(DP)求解,狀態定義為:dp[i]?表示分配i?名同學時能獲得的最大討論積極度之和。初始狀態:dp[0]=0(0名同學時討論積極度為0)。狀態轉移:對于i名同學,枚舉最后一個小組的大小k(1≤k≤i),則剩余i?k名同學的最優解為dp[i?k],因此:![]() 。最終答案為dp[n]。完整參考實現代碼如下:
。最終答案為dp[n]。完整參考實現代碼如下:
n = int(input())??????? #同學總數
a = [0] + [int(i) for i in input().split()]? #n個不同人數學習小組的討論積極度。
dp = [0] * (n + 1)????? #初始化討論度為0
for i in range(1, n+1): #對每一個同學for k in range(1, i+1):dp[i] = max(dp[i], dp[i - k] + a[k]) #狀態轉移公式
print(dp[n])3.2 編程題2
- 試題名稱:最大因數
- 時間限制:6.0 s
- 內存限制:512.0 MB
3.2.1 題目描述
給定一棵有10?個結點的有根樹,這些結點依次以1,2,...,10?編號,根結點的編號為1。對于編號為k(2≤k≤10?)的結點,其父結點的編號為k的因數中除k以外最大的因數。 現在有q組詢問,第i(1≤k≤q)組詢問給定x?,y?,請你求出編號分別為x?,y?的兩個結點在這棵樹上的距離。 兩個結點之間的距離是連接這兩個結點的簡單路徑所包含的邊數。
3.2.2 輸入格式
第一行,一個正整數q,表示詢問組數。
接下來q行,每行兩個正整數x?,y?,表示詢問結點的編號。
3.2.3 輸出格式
輸出共q行,每行一個整數,表示結點x?,y?之間的距離。
3.2.4 樣例
3.2.4.1 輸入樣例1
- 3
- 1 3
- 2 5
- 4 8
3.2.4.2 輸出樣例1
- 1
- 2
- 1
3.2.4.3 輸入樣例2
- 1
- 120 650
3.2.4.4 輸出樣例2
- 9
3.2.5 數據范圍
對于60% 的測試點,保證1≤x?,y?≤1000。
對于所有測試點,保證1≤q≤1000,1≤x?,y?≤10?。
3.2.6 編寫程序思路
分析:題目給出了一棵特殊的樹,其節點編號從1到10?,根節點為1。對于編號為k(k ≥ 2)的節點,其父節點是k的?除k以外最大的因數?。例如:節點2的父節點是1(2的因數有1和2,除2外最大是1);節點3的父節點是1(3的因數有1和3);節點4的父節點是2(4的因數有1、2、4,除4外最大是2);節點6的父節點是3(6的因數有1、2、3、6,除6外最大是3)。特點是質數全連在根結點上,質數與根1的距離為1,質數間距離為2。?路徑長度?:如果兩個節點x和y在樹上的距離是d,那么它們的?最近公共祖先(LCA)?會出現在路徑中。因此,我們可以先找到x和y的LCA,然后計算從x到LCA的距離和從y到LCA的距離,最后相加。如預先計算LCA,則時間復雜度為O(n log n),對后40%數據會超時。
解決方案:由于樹高不超過O(log n),對n=10?樹高不超過30。?對于每個查詢(x, y),先分別求x、y的節點序列直到根節點,再從分別從x、y開始邊計算距離邊找它們的LCA,兩距離和即為結果。如120:節點序列為120,60,30,15,5,1(最小因素2,2,2,3,5),650:節點序列為650,325,65,13,1(最小因素2,5,5,13),LCA為1,120到1的邊數為5,650到1的邊數為4,故距離為9。
找因素的時間復雜度為O(n1?2)?,找LCA求距離的時間復雜度O(log n)。總時間復雜度為O(q*n1?2*log n))。對60%的數據n≤1000,O(q*n1?2*log n))<600*31.63* 9.966=<189135,可忽略;對40%的數據n≤10?時O(q*n1?2*log n)) <400*32000*30=384000000,10?級,基本不會超時。完整參考代碼如下:
q = int(input())???????????????? #節點組數
def factor(x):c = [x] #c[0]為初始節點為x,索引大于0為前一個節點的父節點for i in range(2, int(x**0.5+1e-7)+1): #整數唯一分解定理,因子為不下降序列while c[-1] % i == 0:??? #求最小因數i。c.append(c[-1] // i) #i為最小因素(除以i為最大),添加前一個節點的父節點if c[-1] > 1:??????????????? #最后一個質因素c.append(1)????????????? #添加根節點return c???????????????????? #節點序列for i in range(q): #q組節點對x, y = [int(i) for i in input().split()] #輸入兩個節點a = factor(x)???????? #返回a[0]為x節點,其他為其上的父節點直到根節點1b = factor(y)???????? #返回b[0]為y節點,其他為其上的父節點直到根節點1px, py = 0, 0while a[px] != b[py]: #求x、y到最近公共祖先(a[px]==b[py])距離px、pyif a[px] > b[py]:px += 1else:py += 1print(px + py)

)















如何分析和優化存儲過程?)
)