文章目錄
- 題目
- 遞歸
- 思路
- 細節
- 易錯
- 代碼
- 復雜度分析
- 迭代
- 思路
- 細節
- 易錯
- 代碼
- 復雜度分析
題目
輸入某二叉樹的前序遍歷和中序遍歷的結果,請重建該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重復的數字。
例如,給出
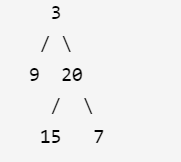
前序遍歷 preorder = [3,9,20,15,7]
中序遍歷 inorder = [9,3,15,20,7]
返回如下的二叉樹:
限制:
0 <= 節點個數 <= 5000
遞歸
思路
首先要明確最重要的一個知識:
對于任意一顆樹而言,前序遍歷的形式總是
[ 根節點, [左子樹的前序遍歷結果], [右子樹的前序遍歷結果] ]
即根節點總是前序遍歷中的第一個節點。而中序遍歷的形式總是
[ [左子樹的中序遍歷結果], 根節點, [右子樹的中序遍歷結果] ]
顯然:
- 對前序遍歷來講,找到左右子樹的遍歷結果分界線是困難的,找到根節點是簡單的
- 對中序遍歷來講,找到根節點是困難的,但找到根節點之后,左右兩側自然分成左右兩棵子樹
根據上面的特性,我們可以做出互補:
- 通過前序遍歷的結果數組的首元素確定根節點
- 根據找到的根節點結合中序遍歷數組確定左右子樹的節點數目
重復上述過程,我們也就可以通過將每個節點視作根節點,不斷遞歸生成左右子樹,無法再生成左右子樹。很顯然生成左右子樹的過程可以用遞歸思想來實現。
細節
思路有了,仍需解決幾個問題:
- 即使通過前序遍歷找到根節點,怎樣確定根節點在中序遍歷中的位置?
- 遞歸生成左右子樹的細節操作是什么?
先解決第一個問題:
普通的方法當然是拿著根節點的值,從中序遍歷結果數組inorder [0]開始遍歷,但是每次在生成根節點時都進行遍歷的話,時間復雜度較高(O(N))。因此可以使用哈希表來建設中序遍歷數組值到下標的鍵值對映射。
在構造二叉樹的過程之前,我們可以對中序遍歷的列表進行一遍掃描(O(N)),就可以構造出這個哈希映射。
在此后構造二叉樹的過程中,我們就只需要 O(1)的時間對根節點進行定位了。(一次O(N),N次O(1));否則我們必須每次都遍歷一遍中序遍歷結果數組定位根節點(N次O(N))。
再來說第二個問題:
遞歸生成左右子樹這種說法聽起來還是太“模糊”了,其實我們實際做的操作是不停的生成根節點,再進入這個根節點的左右子樹,在每個子樹中生成當前子樹的根節點,直到這個”根節點“沒有子樹為止。
易錯
寫代碼的時候沒有子樹應該返回空指針——return nullptr;,粗心大意寫成了return null;,null和nullptr是有區別的。
代碼
class Solution {
private:map<int, int> index; // 映射值給定值對應的下標
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int num = inorder.size();for (int i = 0; i < num; i++){index[inorder[i]] = i; // 建立中序遍歷數組 值到下標 的鍵值對映射,快速定位根節點}return buildRoot(preorder, inorder, 0, num - 1, 0, num - 1);}// 把每個節點都當作它自身的“根節點”,進入到每個節點遍歷生成它的左右子樹、及根節點本身 TreeNode* buildRoot(vector<int>& pre, vector<int>& in, int pre_left, int pre_right, int in_left, int in_right) {if (pre_left > pre_right) { // 沒有子樹return nullptr;}int pre_root = pre_left; // 前序遍歷的根節點就是左邊界int in_root = index[pre[pre_left]]; // 根據映射關系確定中序遍歷中的根節點TreeNode* root = new TreeNode(in[in_root]); // 建立根節點// 等價于TreeNode root = TreeNode(in[in_root]);// TreeNode *proot = &root;// 但沒必要這樣寫,可能便于理解但是過于繁瑣int lefttree_num = in_root - in_left; // 確定左子樹中節點數目// 前序遍歷 根節點(左邊界)+1 到 根節點+左子樹數量 的范圍為左子樹// 中序遍歷根節點左側為左子樹root->left = buildRoot(pre, in, pre_left + 1, pre_left + lefttree_num, in_left, in_root - 1); // 前序遍歷 根節點+左子樹數量+1 到 右邊界 的范圍為右子樹// 中序遍歷根節點右側為右子樹root->right = buildRoot(pre, in, pre_left + 1 + lefttree_num, pre_right, in_root + 1, in_right);return root;}
};
復雜度分析
時間復雜度:O(n),其中 n 是樹中的節點個數。
空間復雜度:O(n),除去返回的答案需要的 O(n)空間之外,我們還需要使用 O(n) 的空間存儲哈希映射,以及 O(h)(其中 h 是樹的高度)的空間表示遞歸時棧空間。這里 h < n,所以總空間復雜度為 O(n)。
迭代
思路
前序遍歷的相鄰節點 u 和 v 有如下關系:
- v 是 u 的左兒子;
- u 沒有左兒子。則 v 是 u 或者 u 祖先節點的右兒子。
以此樹為例:

它的前序遍歷和中序遍歷分別為
preorder = [3, 9, 8, 5, 4, 10, 20, 15, 7]
inorder = [4, 5, 8, 10, 9, 3, 15, 20, 7]
可以看到,對于3,9,8,5,4它們之間滿足第一種關系(例如:8是9的左兒子),對于4,10它們滿足第二種關系,10是4祖父節點的右兒子。
也就是前序遍歷會
- 從根節點開始,一直遍歷左子樹
- 直到左子樹遍歷完了,開始遍歷右子樹
- 如果當前的節點沒有右子樹,則會回溯遍歷祖先節點的右子樹。
那么我們可以根據這一特性,我們可以用一個棧來存儲祖先節點和左子樹,直到左子樹被遍歷完,(本例中,將3,9,8,5,4依次入棧,直到遇到10)此時開始尋找當前節點(10)是誰的右兒子。
細節
思路有了,仍需解決幾個問題:
- 當開始遍歷右子樹,怎么確定當前節點是誰的右兒子呢?
這時來看中序遍歷,我們可以發現,中序遍歷結果數組的首元素是——根節點不斷往左走達到的最終節點。 根據這一特性,我們可以創建一個指針 index 指向當前的最左子樹。
首先我們將根節點 3 入棧,再初始化 index 指向的節點為 4,隨后對于前序遍歷中的每個節點,我們依次判斷它是棧頂節點的左兒子,還是棧中某個節點的右兒子。
- 我們遍歷 9。9 一定是棧頂節點 3 的左兒子。我們使用反證法,假設 9 是 3 的右兒子,那么 3 沒有左兒子,index 應該恰好指向 3,但實際上為 4,因此產生了矛盾。所以我們將 9 作為 3 的左兒子,并將 9 入棧。
stack = [3, 9]
index -> inorder[0] = 4
- 我們遍歷 8,5 和 4。同理可得它們都是上一個節點(棧頂節點)的左兒子,所以它們會依次入棧。
stack = [3, 9, 8, 5, 4]
index -> inorder[0] = 4
- 當我們遍歷到 10,這時情況就不一樣了。我們發現此時 index 指向的節點和當前的棧頂節點一樣,都為 4,也就是說 4 沒有左兒子,那么 10 必須為棧中某個節點的右兒子。 那么如何找到這個節點呢?棧中的節點的順序和它們在前序遍歷中出現的順序是一致的,而且每一個節點的右兒子都還沒有被遍歷過, 那么這些節點的順序和它們在中序遍歷中出現的順序一定是相反的(原因如下)。
這是因為棧中的任意兩個相鄰的節點,前者都是后者的某個祖先。并且我們知道,棧中的任意一個節點的右兒子還沒有被遍歷過(前序遍歷順序——中左右),說明后者一定是前者左兒子,那么后者就先于前者出現在中序遍歷中(中序遍歷順序——左中右)。
因此我們可以先把此時的棧頂元素保存并彈出, 然后把 index 不斷向右移動,并與棧頂節點進行比較。如果 index 對應的元素恰好等于棧頂節點,那么說明上一個被彈出的節點沒有右子樹,且其本身是當前節點的左子樹, 所以重復將棧頂節點保存并彈出,然后將 index 增加 1 的過程,直到 index 對應的元素不等于棧頂節點,此時 index 對應的元素就是上一個被保存且彈出的棧頂節點的右子樹。按照這樣的過程,我們彈出的最后一個節點 x 就是 10 的父節點,這是因為 10 出現在了
x與x在棧中的下一個節點的中序遍歷之間,因此 10 就是 x 的右兒子(根據中序遍歷順序——左中右,x是中,10是右,x在棧中的下一個節點是x的父節點)。
回到我們的例子,我們會依次從棧頂彈出 4,5 和 8,并且將 index 向右移動了三次。我們將 10 作為最后彈出的節點 8 的右兒子,并將 10 入棧。
stack = [3, 9, 10]
index -> inorder[3] = 10
- 我們遍歷 20時。index 恰好指向當前棧頂節點 10,那么我們會依次從棧頂彈出 10,9 和 3,并且將 index 向右移動了三次。我們將 20 作為最后彈出的節點 3 的右兒子,并將 20 入棧。
stack = [20]
index -> inorder[6] = 15
- 我們遍歷 15,將 15 作為棧頂節點 20 的左兒子,并將 15 入棧。
stack = [20, 15]
index -> inorder[6] = 15
- 我們遍歷 7。index 恰好指向當前棧頂節點 15,那么我們會依次從棧頂彈出 15 和 20,并且將 index 向右移動了兩次。我們將 7 作為最后彈出的節點 20 的右兒子,并將 7 入棧。
stack = [7]
index -> inorder[8] = 7
此時遍歷結束,我們構造出了正確的二叉樹。
總結來講就是,遍歷前序遍歷結果數組并將其壓到棧中:
- 當
棧頂元素不等于index指向的元素時,將當前元素作為棧頂元素的左兒子,然后當前元素入棧成為新棧頂。 - 當
棧頂元素等于index指向的元素時,彈出并保存棧頂元素,同時將index遞增1,再判斷棧頂元素和index指向的元素之間的關系,相等則重復上述操作,不相等則將當前元素作為最后一個被彈出的棧頂元素的右兒子,然后將當前元素入棧成為新棧頂。
易錯
- 通過判斷前序遍歷或中序遍歷的結果數組是否為空,來確定二叉樹是否為空。
- 二叉樹不為空時,在建立左右子樹的循環操作之前,先將根節點入棧。因為根節點的建立操作與其他左右子樹不同,放到循環里面要單獨處理,反而繁瑣。
- 注意保存彈出的棧頂元素。
- 在生成右子樹的時候,棧不為空也應該是重要的循環判定條件之一。
代碼
class Solution2 { // 迭代
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if (!preorder.size()) {return nullptr;}stack<TreeNode*> st;TreeNode* root = new TreeNode(preorder[0]); // 建立根節點st.push(root); // 根節點入棧// 否則無法進行將節點歸為左兒子或者右兒子的操作// 因為進行上面的操作需要訪問棧頂元素的left或者rightint index = 0;for (size_t i = 1; i < preorder.size(); i++) {int pre = preorder[i];int in = inorder[index];auto node = st.top();if (node->val != in) { // 如果前序遍歷i位置的數和中序遍歷index位置的數不相等// 說明i位置的數是二叉樹的左子樹node->left = new TreeNode(pre);st.push(node->left);}else {while (!st.empty() && in == st.top()->val) {in = inorder[++index];node = st.top(); // 保存彈出的節點// 當跳出while時,pre的值即為該節點右子樹st.pop();}node->right = new TreeNode(pre);st.push(node->right);}}return root;}
};
復雜度分析
時間復雜度:O(n),其中 n 是樹中的節點個數。
空間復雜度:O(n),除去返回的答案需要的 O(n) 空間之外,我們還需要使用 O(h)(其中 h 是樹的高度)的空間存儲棧。這里 h < n,所以(在最壞情況下)總空間復雜度為 O(n)。

)
)
)

)
)


)









