319. 燈泡開關

初始時有?n 個燈泡處于關閉狀態。第一輪，你將會打開所有燈泡。接下來的第二輪，你將會每兩個燈泡關閉一個。

第三輪，你每三個燈泡就切換一個燈泡的開關（即，打開變關閉，關閉變打開）。第 i 輪，你每 i 個燈泡就切換一個燈泡的開關。直到第 n 輪，你只需要切換最后一個燈泡的開關。

找出并返回 n?輪后有多少個亮著的燈泡。

• 示例 1：

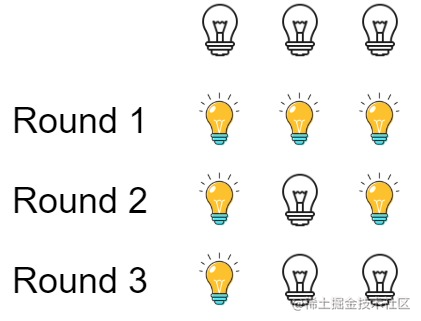
輸入：n = 3
輸出：1 
解釋：
初始時, 燈泡狀態 [關閉, 關閉, 關閉].
第一輪后, 燈泡狀態 [開啟, 開啟, 開啟].
第二輪后, 燈泡狀態 [開啟, 關閉, 開啟].
第三輪后, 燈泡狀態 [開啟, 關閉, 關閉]. 你應該返回 1，因為只有一個燈泡還亮著。示例 2：輸入：n = 0
輸出：0示例 3：輸入：n = 1
輸出：1

解題思路

1. 對于每個燈泡i來說，只要該燈泡被切換開關的次數為奇數次的時候，該燈泡最終會處于亮著的狀態。而該燈泡被切換開關的次數為偶數次的時候，該燈泡最終會處于不亮著的狀態
2. 對于第i個燈泡來說，能出現開關改變的情況，只能出現在其約數x的輪次中，例如第3個燈泡，3的約數為1和3，因此若想被改變只能在第一輪和第三輪中進行修改，并且我們發現約數往往都是成對例如8的約數為1，8，2，4.也就是說往往都是偶數的，而其中的特例就是一些完全平方數，例如9的約數為1，9，3，因為3*3=9，但是因為兩個約數是相同的，因此完全平方數就會產生奇數個約數。
3. 因此，我們需要統計的是完全平方數的個數，只需要通過sqrt(n)求出完全平方數的個數即可。

代碼

class Solution {
public:int bulbSwitch(int n) {return sqrt(0.5+n);}
};