391. 完美矩形

給你一個數組 rectangles ，其中 rectangles[i] = [xi, yi, ai, bi] 表示一個坐標軸平行的矩形。這個矩形的左下頂點是 (xi, yi) ，右上頂點是 (ai, bi) 。

如果所有矩形一起精確覆蓋了某個矩形區域，則返回 true ；否則，返回 false 。

示例 1：

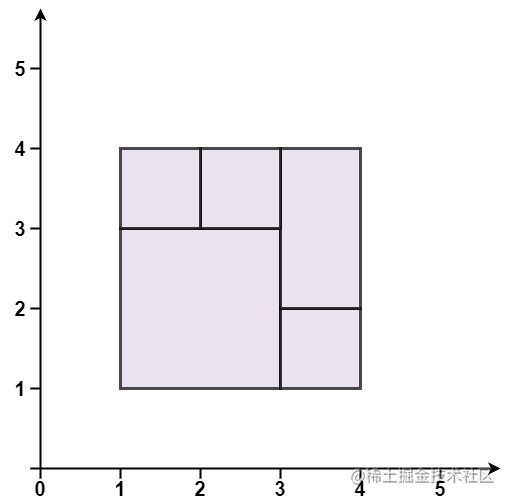
輸入：rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
輸出：true
解釋：5 個矩形一起可以精確地覆蓋一個矩形區域。
示例 2：

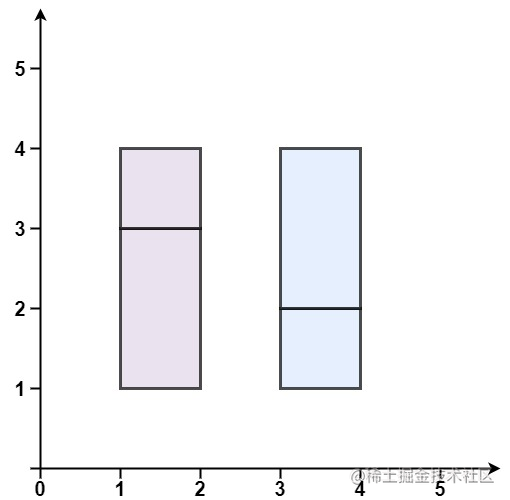
輸入：rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
輸出：false
解釋：兩個矩形之間有間隔，無法覆蓋成一個矩形。
示例 3：

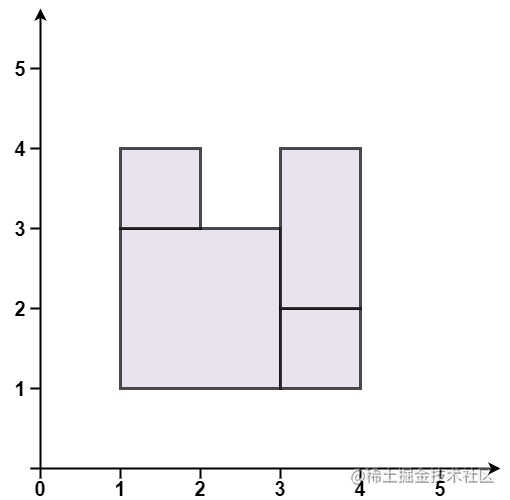
輸入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]
輸出：false
解釋：圖形頂端留有空缺，無法覆蓋成一個矩形。
示例 4：

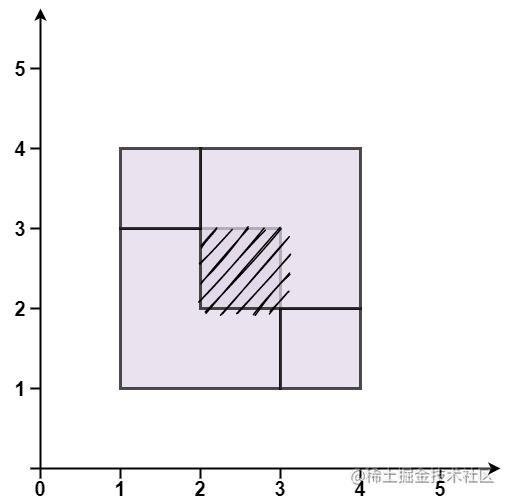
輸入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
輸出：false
解釋：因為中間有相交區域，雖然形成了矩形，但不是精確覆蓋。

提示：

• 1 <= rectangles.length <= 2 * $10^4$
• rectangles[i].length == 4
• $?10^5$ <= xi, yi, ai, bi <= $10^5$

解題思路

首先所有矩形需要組合成一個大的正常矩形，因此矩形之間不能存在空缺。并且因為矩形之間如果存在相交區域，雖然形成了矩形，但就不是精確覆蓋了。

1. 因此我們需要保證所有小矩形加起來的面積等于大矩形
2. 其次如果我們要保證沒有重疊的部分，就需要統計每個頂點出現的次數，除了大矩形的四個頂點以外，每個頂點只能出現2次或者4次。如下圖所示，如果出現了重疊的部分，那么就會出現出現次數為1的頂點
   

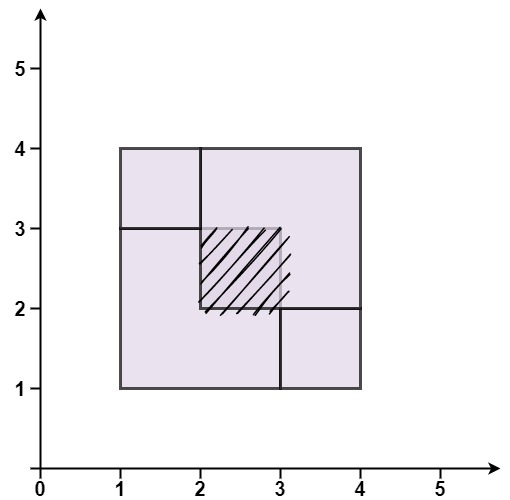
因此，在算法中，我們需要統計每個小矩形頂點的出現次數和其面積，只有當其滿足上述兩個條件，才能實現精準覆蓋

代碼

typedef pair<int, int> point;class Solution {
public:bool isRectangleCover(vector<vector<int>> &rectangles) {map<point, int> m;long long area(0);int min_x1(rectangles[0][0]),min_y1(rectangles[0][1]),max_y2(rectangles[0][3]),max_x2(rectangles[0][2]);for (auto p:rectangles) {int x1 = p[0], y1 = p[1], x2 = p[2], y2 = p[3];min_x1=min(x1,min_x1);min_y1=min(y1,min_y1);max_x2=max(x2,max_x2);max_y2=max(y2,max_y2);m[{x1,y1}]+=1;m[{x1,y2}]+=1;m[{x2,y1}]+=1;m[{x2,y2}]+=1;area+=abs(x1-x2)*abs(y1-y2);}point p1{min_x1,min_y1},p2{min_x1,max_y2},p3{max_x2,min_y1},p4{max_x2,max_y2};if ((long long )abs(min_x1-max_x2)*(long long )abs(max_y2-min_y1)!=area||!m.count(p1)||!m.count(p2)||!m.count(p3)||!m.count(p4))return false;m.erase(p1);m.erase(p2);m.erase(p3);m.erase(p4);for(auto item:m){if (item.second!=2&&item.second!=4)return false;}return true;}
};