第12章 因子投資中的機器學習

12.1 量化金融中的人工智能

隨著機器學習和人工智能在諸多領域取得重大突破，尤其是以GPT為代表的生成式AI模型展現出令人驚嘆的潛力，因子投資的學術界與業界都渴望借助機器學習算法的強大能力來提升因子投資策略。越來越多充滿熱情的實踐者開始探索AI算法的應用，但必須清醒認識到：當前AI工具在基礎自動化與初級分析方面雖已取得長足進步，但試圖讓AI直接做出投資決策或真正理解金融市場運行機制的努力尚未取得顯著成功。

• 卷積神經網絡（CNN）和循環神經網絡（RNN）是兩種對金融市場建模分析做出重要貢獻的深度學習架構。
  • CNN專為處理網格狀數據（如圖像或時間序列）設計，通過卷積運算捕捉局部特征。
    • 其卷積層對輸入數據的局部區域施加濾波器，提取空間或時間模式，從而自動從數據中學習從低級到高級的層次化特征表達。
    • 金融領域，CNN已被應用于股價預測、異常檢測和情感分析等任務，能夠從歷史價格數據、新聞文本或社交媒體情緒中提取有效模式，提升預測準確性并識別市場趨勢。
  • RNN則擅長捕捉序列依賴性，特別適合處理具有時序關聯的數據。
    • 通過內部記憶機制，RNN能保留歷史輸入信息并用于逐步預測，使其在股市預測、組合優化和信用風險評估等任務中表現卓越。
    • STM和GRU等RNN變體通過門控機制有效解決了長期依賴問題。利用金融數據的時間動態特性，RNN能建模復雜關系并揭示隱藏模式，從而提升金融預測與決策的準確性。
• CNN與RNN的混合架構（如ConvLSTM）在金融建模中展現出獨特優勢——先用CNN提取局部特征，再通過LSTM層捕捉時序依賴。該方法在金融時間序列預測、欺詐檢測和算法交易等領域成效顯著。
• 通過CNN和RNN，金融模型能夠自動從復雜數據中學習有效特征，建模空間、時間和序列關系，提供更精準的預測與洞察。
• 但需注意，這些架構的成功應用高度依賴數據質量、預處理技術以及穩健的模型訓練驗證流程。

從本書的核心關切——也是因子投資必須考量的數據分布變化問題——我們就能理解為何將金融決策權交給AI是極具挑戰的任務。當前取得輝煌成功的算法多屬歸納法，即從數據相關性中推導規律。AI在圖像和文本的識別、理解與生成方面固然取得驚人進展，但必須認識到：未來數據分布可能發生變化，這將瓦解對歷史數據分布觀測的依賴。讀者可參閱本書$第10章$了解分布不確定性何時出現，進而理解機器學習的局限性。

數學上，這暗示數據生成過程具有時變性。金融研究中常見現象包括：某些模式或因子隨時間推移失效；在發達股市有效的因子在新興市場呈現相反效應（如中美股市中的動量因子差異）。因此，算法智能生成的核心難題或許在于應對數據生成過程的分布變化。

此外，我們接觸的數據往往存在偏差且不能代表整體樣本空間。例如，分析醫院患者數據可能得出"就診者死亡率高于普通人群"的悖論，但這顯然不能推導出"就醫導致病情惡化"的結論——因為只有不適者才會就醫。要分析就醫效果，還需獲取不適卻未就醫人群的健康數據。 回到因子投資，我們使用的歷史數據僅是人類歷史的微小片段。以近年美股由科技巨頭驅動持續上漲為例，這種市場結構可能導致訓練數據識別的因子偏向大市值股票，誤將市值作為有效預測變量。但是，長期視角顯示，小市值股票往往能獲得更高超額收益（即著名的小市值因子）。

數據生成過程的分布變化可能性和觀測數據的偏差，使得未經改造的機器學習算法直接在金融領域應用難以成功。中國古代兵家智慧有云，“為將者未慮勝先慮敗”，深刻揭示了認識并準備應對失敗可能性的重要性。

我們不惜篇幅討論這些核心問題，因為理解機器學習應用于投資的困難，是開發新技術克服或緩解這些挑戰、或尋找折中方案繞開它們的第一步。這些問題可能將長期作為重要學術難題存在，其啟示在于：運用先進AI算法進行因子投資時，不應拋棄因子研究的邏輯分析——事實上因子背后的邏輯更需要被重視。因子僅是股票屬性的量化表征，理解這些表征背后的原理才至關重要。事實上，鑒于金融數據存在諸多機器學習模型假設的違背、低信噪比和非平穩性（Nagel 2021），用經濟理論指導機器學習算法正是其成功的關鍵。

本章將從機器學習視角全面闡釋因子投資的現狀與未來，為讀者提供前瞻性思考。具體安排如下：

12.2節 討論機器學習如何應用于因子投資實踐全流程；
12.3節 深入解析機器學習在實證資產定價和因子投資應用的最新進展；
12.4節 聚焦因子發現這一關鍵問題與機器學習的可能角色；
12.5節 對比因子投資中的機器學習與計量經濟學方法；
12.6節 總結全文。

12.2 量化因子投資的AI化組件：解剖學視角

本節首先采用分析視角，解構量化因子投資全流程的主要階段，思考每個階段如何引入機器學習算法。按此思路，我們逐步分析各環節，初步識別算法能顯著提升投資實踐的領域。

12.2.1 數據源拓展與預處理

除傳統結構化金融數據外，蘊含豐富市場與個股信息的非結構化數據亟待挖掘。AI可優化信息收集的全面性與及時性，基于GPT的工具能提供重要助力。

AI算法還能實時監控數據質量與異常。在非結構化數據（如新聞情緒或公司知識圖譜）的信息提取中（Bybee, Kelly and Su 2023; Bybee et al. forthcoming），AI擅長從文本與圖像中提取具有股票收益預測信息的量化指標。

此外，數據預處理中的智能化數據庫工程（如數據更新、校驗、缺失值填充（Freyberger et al. 2021; Bryzgalov et al. 2022）、向量化查詢、負載均衡存儲與分布式計算）也是AI算法的用武之地。

12.2.2 因子研究

因子研究的核心在于因子發現。因子邏輯的自動化挖掘與提取是極具前景的AI應用方向，但需要大量工程與學術支持以實現進一步發展。本章12.4節將深入探討。

12.2.3 因子模型

為解釋資產或組合橫截面預期收益，各類定價模型被提出、討論，金融學術界逐漸形成基于機器學習的研究范式（12.3節將詳述）。

當識別出大量預測因子后，如何有效整合形成可交易信號成為關鍵。

高維度和因子間相關性帶來重大挑戰，這為機器學習算法提供了廣闊應用空間。

此外，復雜因子組合模型中可納入市場環境變量，希望通過復雜模型的非線性擬合能力增強現有線性因子。當然，需警惕模型復雜度提升導致的過擬合風險，通過$必要正則化$等技術進行防控。

12.2.4 風險分析與組合優化

生成收益預測信號后，組合風險分析是核心環節。

理解收益源于特定風險承擔，風險控制優化的核心目標是在預設風險約束下最大化收益。

新興研究方向包括：建立強化學習模型與模擬環境，基于資產定價模型設定風險暴露水平，定義動作空間（股票買賣），訓練強化代理根據預測信號與定義的風險控制懲罰進行優化。

12.2.5 交易執行與監控

量化研究分析后的最終環節是實際交易執行。該過程存在大量優化機會，如前文提到的流動性對交易執行的影響。

反映短期股價走勢的高頻數據可用于開發交易算法。由于優化交易執行算法的數據頻率更高，數據分布變化程度相對較小，可采用復雜算法解析市場微觀結構與短期供需動態。

12.3 機器學習與資產定價

自Gu, Kelly和Xiu(2020)將機器學習方法正式引入實證資產定價研究以來，過去幾年學術界大量學者應用各類機器學習模型（線性和非線性）進行股票收益預測，并識別應納入定價模型或隨機貼現因子(SDF, stochastic discount factor)的因子。Kelly和Xiu(2023)提供了精彩綜述。

這一轉變主要源于因子數量的指數級增長及因子與資產收益間復雜關系——這是大數據與機器學習時代的典型特征。這些發展對基于計量方法的傳統實證研究提出了重大挑戰。雖然計量技術仍是分析簡單線性關系和參數判定的有力工具，但在處理高維預測問題時并非首選方案（12.5節將詳細對比機器學習與計量經濟學）。已在自然語言處理和圖像識別等領域驗證為有效的機器學習算法，自然成為了解決此類復雜問題的選擇。

因此，學術研究明顯從提出簡約而特殊的多因子模型（以減少市場異象為目標），轉向日益突出的機器學習方法。這催生了圍繞多因子模型和隨機貼現因子(SDF)的新研究范式，研究導向悄然從"程序性"開發轉向"實證性"驅動。采用機器學習算法進行資產定價的論文大量發表于頂級期刊是最有力的證據。同時，各類機器學習算法已進入因子投資的行業實踐，尤其在因子發現與聚合方面。

回望學術研究，深入審視這些實證工作可發現，它們在理論闡述與實證結果方面存在大量共性。精讀這些文獻能極大提升我們對機器學習算法應用于實證資產定價和因子投資的理解。本節旨在為讀者客觀呈現該領域現狀，通過五組事實與虛構的討論，厘清機器學習與資產定價的真相與誤解。

12.3.1 虛構1：數據會"自己說話"

第一個虛構觀點認為：只需將數據盲目輸入復雜機器學習算法，單純期待數據"自己說話"。

金融數據固有的低信噪比和非平穩性，足以打破"對金融數據直接套用現成機器學習 就能獲得有意義洞見"的天真幻想。
在資產定價領域，參數先驗分布、協變量縮放、正則化懲罰和調優標準選擇等諸多方面都會顯著影響結果。

• Nagel(2021)的示例雖簡單但有效地闡明了上述考量：假設用過去120天收益及其平方、立方值作為協變量，預測次日收益。
• 表12.1總結了不同設置下的預測結果，其中：
  • Method列表示采用的正則化方法（OLS表示無正則化）
  • Scaling列顯示協變量標準化方式
    • Equal表示所有協變量標準化為均值0、標準差1
    • Unequal表示標準化后標準差不同
  • CV Criterion列表示交叉驗證采用的指標（如R平方或組合預期收益）。
  • 表中OLS指普通最小二乘法，IS指樣本內，CV指交叉驗證。

Method	Scaling	CV Criterion	IS $R^2$	CV $R^2$	CV Portfolio Sharpe Ratio
OLS	Equal	N/A	5.22%	-1.18%	0.35
Ridge	Equal	$R^2$	2.63%	0.84%	0.30
Ridge	Unequal	$R^2$	2.69%	1.18%	0.37
Ridge	Unequal	$E[r_p]$	1.75%	0.89%	0.35
Lasso	Unequal	$R^2$	3.55%	0.84%	0.36

表12.1 收益預測示例 數據來源：摘編自Nagel(2021)表3.2

• 實證結果顯示，模型設定對結果影響顯著。
• 但面對海量選項時，窮舉所有排列組合既不現實也不明智，關鍵在于有效利用金融理論衍生的先驗知識。
  • 例如：
    • 若假設模型非稀疏，可能選擇嶺回歸而非Lasso；
    • 若認為協變量對收益預測重要性不同，可能選擇非等比例縮放；
    • 若從金融理論核心出發，可能選擇優化夏普比率（或最小化定價誤差）而非傳統R平方。
  • 這些決策本質上都源于資產定價理論。

12.3.2 事實1：在資產定價框架內應用機器學習

與虛構1相反，第一個事實指出：我們應在資產定價理論框架內運用大數據與機器學習算法。

實證資產定價領域從CAPM到APT/ICAPM，再到龐雜的因子動物園，無疑通過大量實證挑戰推動了學科發展。盡管范式幾經變遷，但研究核心始終圍繞資產定價理論展開。例如Bryzgalova, Pelger和Zhu（即將發表）與Chen, Pelger和Zhu(2023)這兩篇近期重要論文，前者采用決策樹，后者運用生成對抗網絡(GAN)，但都將SDF框架作為應用不同算法于資產定價的基礎。

類似地，Kelly, Pruitt和Su(2019)的工具化主成分分析(IPCA)與Gu, Kelly和Xiu(2021)的自編碼器模型，都采用潛在因子模型，將因子暴露(β)建模為協變量（如公司特征與宏觀經濟變量）的函數。二者區別在于，前者使用線性模型，后者選擇非線性模型。且由于協變量具有時變性，這兩種方法本質上都屬于條件定價模型。

實證上，這些研究的共同點是，使用遠超傳統研究數量的協變量，并通過組合樣本外表現，從而驗證方法的有效性。盡管這些論文嘗試不同機器學習算法，但鑒于SDF與多因子模型的等價性，其方法可在統一框架下檢視理解，展現了先進機器學習技術與基礎資產定價理論的融合。

12.3.3 虛構2：機器學習模型忽視可解釋性

第二個虛構觀點認為：機器學習模型是黑箱，學術研究忽視可解釋性。

可解釋性是傳統多因子模型或異象研究的精髓。例如Fama和French(2015)五因子模型基于股利貼現模型，Hou, Xue和Zhang(2015)的$q因子模型$則立足$q理論$。異象論文也提供解釋，將其歸類為風險補償或錯誤定價。當研究目標轉向通過復雜模型更準確預測資產收益時，似乎產生"弱化可解釋性重視程度"的誤解，但事實并非如此。

對線性模型（如Kozak, Nagel和Santosh(2018,2020)的主成分分析和Kelly, Pruitt和Su(2019)的IPCA），可解釋性相當直觀。
前者發現：對規模和價值構建的25個組合進行PCA得到的前兩個主成分(PC)，完美對應小減大（規模）和高減低（價值）因子。
后者雖數學表達復雜，但其底層直覺本質上是通過橫截面回歸構建管理組合的線性組合。
因此對線性模型，其可解釋性深深植根于人們熟悉的回歸與組合排序。

對非線性模型，其可解釋性雖不如線性模型直觀，但學術研究仍高度重視（事實2將討論）。探究模型預測背后的"原因"與"機制"始終是基本追求，確保即使最復雜的模型也致力于實現一定程度的透明性與清晰解釋，符合學術研究不僅追求預測準確性，也追求可理解洞察的目標。

12.3.4 事實2：機器學習揭示關鍵預測變量

作為對虛構2的回應，第二個事實指出：機器學習揭示了與大量實證資產定價發現相吻合的最重要預測變量。

Gu, Kelly和Xiu(2020)通過排列重要性識別對解釋預期收益最關鍵協變量，發現：

1. 最重要協變量與既往實證發現一致，主要分為動量/反轉、流動性相關、風險相關（如 idiosyncratic volatility）和基本面四大類（注意，這些都是本書論述的重要因子）；
2. 不同機器學習模型的最重要協變量高度重疊。

此外，Chen, Pelger和Zhu(2023)通過計算SDF權重對協變量的偏導數評估模型可解釋性，發現所有協變量中影響力最大者涉及交易摩擦、價值、無形資產、盈利能力、投資和歷史收益等方面。

另一值得關注的是Kozak(2019)，其巧妙運用核技巧，將協變量映射到高維空間而不增加計算復雜度，再對這些轉換后協變量進行PCA。非線性核的使用模糊了轉換后協變量的性質，但通過將構建的SDF映射回原始協變量的管理組合，仍可識別最重要的解釋變量。

最后，如Avramov, Cheng和Metzker(2023)所示，通過觀察不同協變量下選定股票的共性特征，也能推斷某些變量的重要性。

這些方法印證了機器學習衍生的預測因子與大量實證資產定價結果的一致性，在數據驅動的金融創新景觀中確認了基礎原則的連續性。

12.3.5 虛構3：復雜模型必然導致糟糕樣本外表現

• 初看虛構3，似乎合理：復雜模型容易樣本內過擬合，導致樣本外預測誤差大幅增加。
• 該觀點認為隨著模型復雜度提升，其捕捉和復制樣本內數據細微特征的能力增強，可能以犧牲對未見數據的泛化能力為代價。
• 這一論述基于對模型復雜度及其與欠擬合、過擬合關系的傳統理解。
  • 低復雜度時，模型傾向欠擬合，表現為低方差、高偏差；
  • 復雜度增加時，偏差降低但方差增加，導致過擬合。
  • 這種相互作用被稱為偏差-方差權衡，暗示存在使樣本外誤差（即測試風險）最小化的最優超參數集。
  • 參見圖12.1左側展示這一經典U型關系。

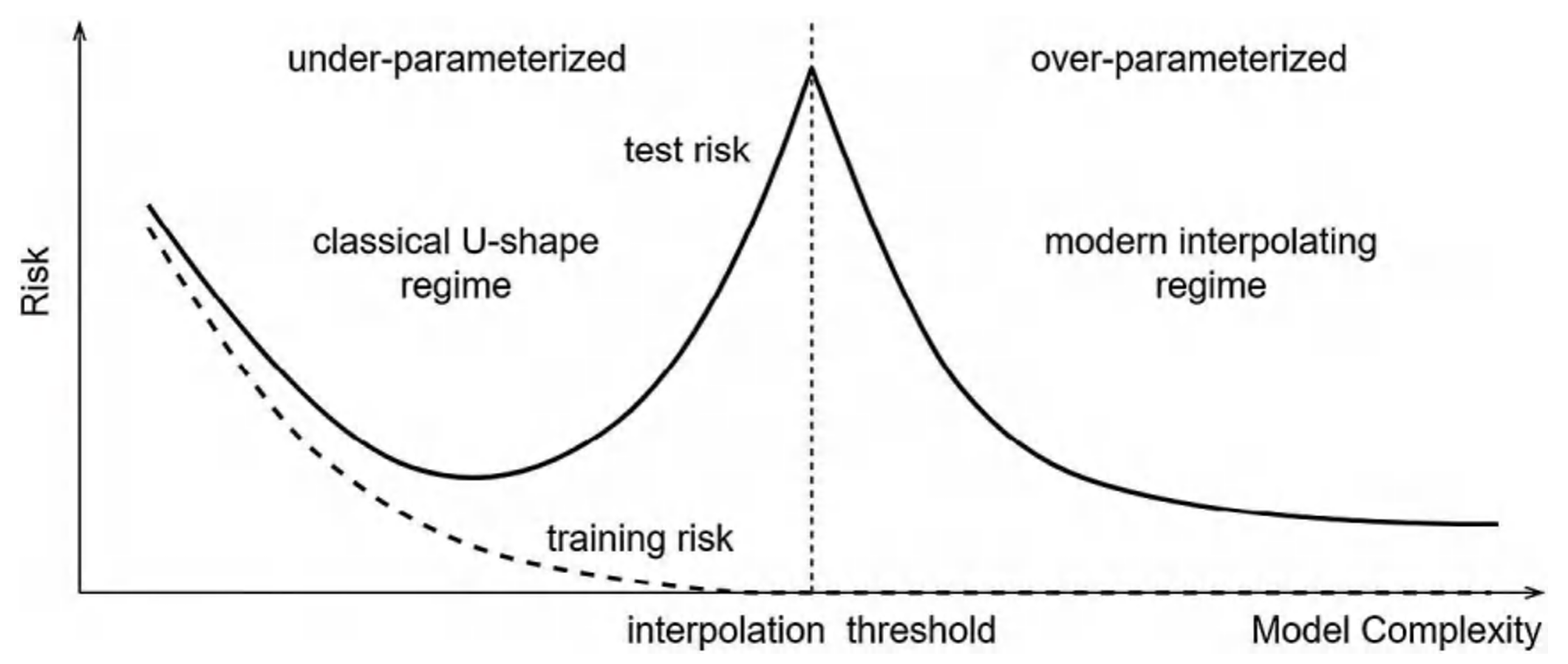
圖12.1 風險 vs. 模型復雜度

• 這種權衡也可從另一視角理解：
  • 簡單模型善于避免過擬合，但可能無法準確近似真實世界；
  • 復雜模型或許更接近現實世界現象，但確實更容易過擬合。
• 因此偏差-方差權衡也可解讀為近似-過擬合權衡。
• 機器學習與統計建模的傳統智慧由此認為：參數過多（即參數量遠超訓練數據量）會導致過擬合，因為模型會學習訓練數據中的噪聲而非底層模式。
• 因此，通常建議模型參數量應遠小于訓練數據量。

但在深度學習領域，這一傳統智慧并不總成立。盡管參數量常超過訓練數據量，但深度學習模型被發現對未見數據具有良好的泛化能力。這一現象常被稱為**"雙下降"曲線**（Loog等2020），顯示當參數量超過訓練數據規模后，模型測試性能可能再次提升。

該現象原因仍是研究熱點。有理論認為，深度學習模型結構和訓練算法的非凸優化特性具有隱式正則化效果；也有觀點認為，過參數化模型能表達更廣闊函數空間，增加找到同時擬合訓練數據且泛化良好模型的機會。盡管尚無定論，過參數化深度學習模型的有效性已是實證事實。

12.3.6 事實3：適當正則化下模型復雜度收益超越統計代價

機器學習理論發展有力反駁了虛構3，指出復雜模型能更準確逼近真實數據生成過程(DGP, data generating process)。只要施加足夠正則化，模型復雜度帶來的優勢可能超越過參數化的統計代價。

近年來機器學習領域最激動人心的發現正是雙下降現象——樣本外誤差與模型復雜度呈現非單調關系。如Belkin等(2019)指出：當模型復雜度突破樣本量限制時（傳統認為應避免的區域），樣本外總誤差非但沒有"爆炸"，反而隨復雜度增加開始單調下降（如圖12.1右側所示）。這種在插值閾值兩側均呈現誤差單調下降的現象被命名為雙下降。

該現象直覺在于：當協變量數量超過樣本量時，樣本內解不再唯一。
最優解可理解為參數方差最小的解。
隨著模型復雜度提升，最優解方差降低。
此外，需注意所有模型都是真實DGP的某種誤設。當存在模型誤設時，可以證明在變量數超過樣本量的特定范圍內，偏差也可能隨復雜度增加而降低。綜合效應導致測試風險下降。
對雙下降理論基礎感興趣的讀者可參閱Hastie等(2022)的詳細討論。

在實證資產定價中，Kelly、Malamud和Zhou(2024)將這一概念應用于美股市場擇時，觀察到類似雙下降現象：當協變量數量遠超樣本量時，樣本外夏普比率得到改善。Didisheim等(2023)進一步將該思想拓展至橫截面，研究因子定價模型中的復雜度問題。

雖然機器學習理論最新進展令人振奮，但需注意關于模型復雜度與樣本外表現的討論仍處起步階段。正則化在此過程中至關重要，該領域有待更多研究。

12.3.7 虛構4：非線性模型可輕易實現夏普比率翻倍

虛構4指錯誤認為非線性模型可輕易實現夏普比率翻倍。但是，讓我們先檢視一組看似支持該觀點的有力實證結果。

Baba-Yara、Boyer和Davis(2021)復制了近年來一些主要機器學習資產定價模型，并與傳統因子模型比較性能。表12.2匯總了部分代表性結果。

機器學習模型	機器學習模型	傳統因子模型	傳統因子模型
模型	OOS夏普	模型	OOS夏普
BPZ隨機森林	2.19	FF3	0.45
Davis神經網絡	3.21	FF5+MOM	1.03
KNS PCA	3.21	Hou-Xue-Zhang	1.10
KPS IPCA	3.39	Stambaugh-Yuan	0.61

表12.2 機器學習與傳統因子模型比較 數據來源：摘編自Baba-Yara等(2021)

結果生動地顯示了：相比傳統因子模型，機器學習模型實現的夏普比率確實達到傳統模型兩倍甚至三倍。但需牢記，傳統模型是稀疏的，構建因子時使用的協變量少得多。這種比較本質上不公平。（我們將在事實4重新審視這些結果。）

另一方面，細看可發現上述結果中PCA和IPCA模型（均為非條件線性模型）的夏普比率實際上高于采用隨機森林和神經網絡等非線性模型的成果。這似乎表明至少在引用的實證結果中，非線性模型未必優于線性模型。

12.3.8 事實4：非線性模型提供邊際增量貢獻

毫無疑問，協變量與資產收益間存在非線性關系。但在現階段，非線性模型更可能提供解釋橫截面的邊際增量貢獻。

如Nagel(2021)和大量近期實證資產定價研究所示，變量間交互作用在這些非線性關系中至關重要。對傳統線性回歸模型，隨著變量增加，考慮所有協變量對的交互項變得不切實際。這為擅長處理非線性關系的機器學習模型提供了機會。

但對非線性關系帶來的收益預測增量貢獻需保持現實預期。Chen、Pelger和Zhu(2023)的實證發現表明：他們的GAN在構建SDF時能捕捉協變量間交互作用，但也強調單個協變量對SDF的影響幾乎呈線性。

現在重新審視虛構4提到的Baba-Yara等(2021)研究。他們早期版本論文的實證期間為1990-2020年，而最新版本卻奇怪地縮短為1990-2016年。更令人困惑的是作者解釋稱比較的傳統模型之一Stambaugh-Yuan模型數據僅更新至2016年。但若早期版本能研究至2020年，為何新版本要回退至更早截止日期？真實動機不得而知。

機器學習模型	OOS夏普(2020)	傳統因子模型	OOS夏普(2020)
BPZ隨機森林	0.86(2.19)	FF3	0.61(0.45)
Davis神經網絡	2.39(3.21)	FF5+MOM	1.17(1.03)
KNS PCA	2.77(3.21)	Hou-Xue-Zhang	1.81(1.10)
KPS IPCA	3.21(3.39)	Stambaugh-Yuan	1.40(0.61)

表12.3 機器學習與傳統因子模型比較(II) 數據來源：摘編自Baba-Yara等(2021)

在這個縮短的實證期間，結果匯總于表12.3（括號內為截至2020年的結果，供比較）。耐人尋味的是：當實證截止期設為2016年，四個機器學習模型均出現不同程度惡化，而四個傳統模型全部改善。

聚焦機器學習模型，這些比較顯示不同實證期間結果存在顯著波動。同時，盡管這些研究采用滾動或擴展窗口進行訓練驗證后才預測下一年樣本外收益，但關于調參過程及不同超參數下模型穩健性的討論極少（如果有的話）。這方面應用機器學習于資產定價的研究生態遠未成熟，亟需領域領導者建立公認研究規范。

12.3.9 虛構5：機器學習模型可輕松付諸實踐

最后一個虛構觀點認為，機器學習模型可輕松在實踐中應用。雖然機器學習模型在資產定價學術研究中取得了鼓舞人心的成果，但并不意味著能輕松在實踐中獲得扣除所有成本后的顯著超額凈收益。

這方面最關鍵實證發現之一是機器學習模型構建組合的高換手率。Avramov、Cheng和Metzker(2023)復制了文獻中多個領先機器學習模型，包括Gu、Kelly和Xiu(2020)的神經網絡、Chen、Pelger和Zhu(2023)的GAN、Kelly、Pruitt和Su(2019)的IPCA，以及Gu、Kelly和Xiu(2021)的條件自編碼器。這些模型的平均月換手率如表12.4所示。
作為參照，傳統低頻風格因子（如規模和價值）通常月均換手率低于10%（即0.1）。
通過交易成本估算，Avramov等(2023)指出在這種高換手下，投資者難以通過機器學習模型獲得額外超額收益（盡管不排除部分成熟投資者能成功改造這些模型在高換手下實現超額收益）。

模型	月均換手率
Gu、Kelly和Xiu(2020)	0.976
Chen、Pelger和Zhu(2023)	1.664
Kelly、Pruitt和Su(2019)	1.186
Gu、Kelly和Xiu(2021)	1.565

表12.4 機器學習模型換手率

為解決交易成本挑戰，Jensen等(2022)提出"可實施有效前沿"概念，通過考慮成本后收益直接評估策略。該方法將包含交易成本的組合優化問題整合到機器學習框架，取得良好效果。這一進展凸顯在投資策略中部署機器學習模型時考慮交易成本等實際約束的必要性，揭示了學術成功與實際應用間的微妙差距。

12.3.10 事實5：對部分機構投資者價值有限

與虛構5相反，事實是：先進機器學習模型揭示的預測能力部分集中于高套利成本和高交易成本股票，因此對部分機構投資者的價值有限。

實證發現表明，許多異象的超額收益主要來源于空頭端(Avramov等2013)或極小市值股票(Novy-Marx和Velikov2016)。類似地，機器學習模型展現出從高套利成本和高交易成本股票中提取預測能力的長處，這削弱了其實用性。

以Avramov、Cheng和Metzker(2023)的實證結果為例，除全樣本外還檢驗三個子樣本：剔除極小市值股票、無信用評級公司和財務困境企業。結果（表12.5，括號內為t統計量）顯示主流機器學習模型（IPCA除外）在這些子樣本中相比全樣本表現顯著下降。此外，部分機器學習模型相對于FF5+MOM基準的alpha在某些子樣本中不再顯著。

模型	全樣本	剔除極小市值	剔除無信用評級	剔除財務困境
面板A：絕對收益(%)
Gu、Kelly和Xiu(2020)	1.56	1.05	1.02	0.72
	(4.53)	(3.24)	(3.18)	(2.49)
Chen、Peiger和Zhu(2023)	2.13	1.08	0.82	0.92
	(6.37)	(4.06)	(2.83)	(2.91)
Kelly、Pruitt和Su(2019)	0.95	0.91	0.89	0.73
	(5.62)	(5.57)	(5.08)	(4.08)
Gu、Kelly和Xiu(2021)	1.16	1.11	0.87	0.67
	(4.17)	(4.22)	(2.97)	(2.22)
面板B：相對FF5+MOM的alpha(%)
Gu、Kelly和Xiu(2020)	0.92	0.31	0.43	0.20
	(4.08)	(1.51)	(2.05)	(0.92)
Chen、Peiger和Zhu(2023)	1.87	0.55	0.42	0.57
	(4.86)	(2.23)	(1.46)	(1.82)
Kelly、Pruitt和Su(2019)	0.62	0.61	0.61	0.43
	(3.31)	(3.71)	(3.38)	(2.37)
Gu、Kelly和Xiu(2021)	0.75	0.39	0.19	0.05
	(3.01)	(2.03)	(0.79)	(0.20)

表12.5 不同樣本中模型表現 數據來源：摘編自Avramov等(2023)

例如，GAN模型在剔除極小市值股票子樣本中的月收益相比全樣本下降超50%。
在檢驗的四個模型中，除IPCA（線性模型）外，其余非線性模型中僅IPCA在全樣本和各子樣本中表現穩健。

值得注意的是，子樣本結果仍使用全樣本訓練模型得出，這可能引發部分讀者擔憂。
對此，Avramov等(2023)進一步使用子樣本訓練并進行樣本外預測，發現結果無實質變化，甚至某些子樣本中樣本外表現下降。
換言之，約束模型從目標樣本學習的意圖，反而因樣本量減少導致樣本外表現更差。

這些結果暗示：成功改造非線性模型使其聚焦于低套利成本和低交易成本股票，將是機器學習模型在資產定價中實際應用的關鍵前提。

12.4 自動化因子發現

隨著人工智能算法持續進步，利用算法進行因子發現以替代人工操作的興趣日益增長。本節探討這一方法的可行性。

12.4.1 端到端因子擬合

可能首先想到（雖非我們最推薦）的是，直接采用深度學習模型進行端到端因子訓練。深度學習模型具有強大的擬合能力，梯度可提供快速搜索解的優化方向。此方法中，直接預測股票收益可作為目標，但這常導致模型輸出過度相似和過擬合。

更有效的方法可能是基于金融邏輯設定眾多中間目標。該方法通過多樣化目標和為每個目標單獨建模，可增強模型輸出多樣性、并允許調整預測目標。*例如，模型可預測股票基礎屬性（如換手率、波動率、股票間相關性或收益分布），或更復雜的預測如每股收益、投資者情緒或財報提前發布概率等。*預測目標應利用人們對金融市場的理解，部分目標可根據數據可獲得性由模型預測。

此外，可采用無監督學習方法提取股票收益的潛在信息，如使用編碼器-解碼器架構。該方法將因子視為股票潛在信息的量化描述，但缺點在于缺乏對模型預測的透明理解和潛在錯誤的識別。盡管可采用必要技術防控過擬合，但其仍是固有風險。

12.4.2 自動化符號化因子

除直接模型擬合外，對量化因子研究者更復雜但可靠的方法是挖掘數據-算子組合。本書討論的許多金融邏輯因子可分解為多個子邏輯，每個子邏輯通過算子應用于一個或多個變量。這種逐步邏輯鏈可表達復雜因子。圖12.2通過示例說明這一概念。

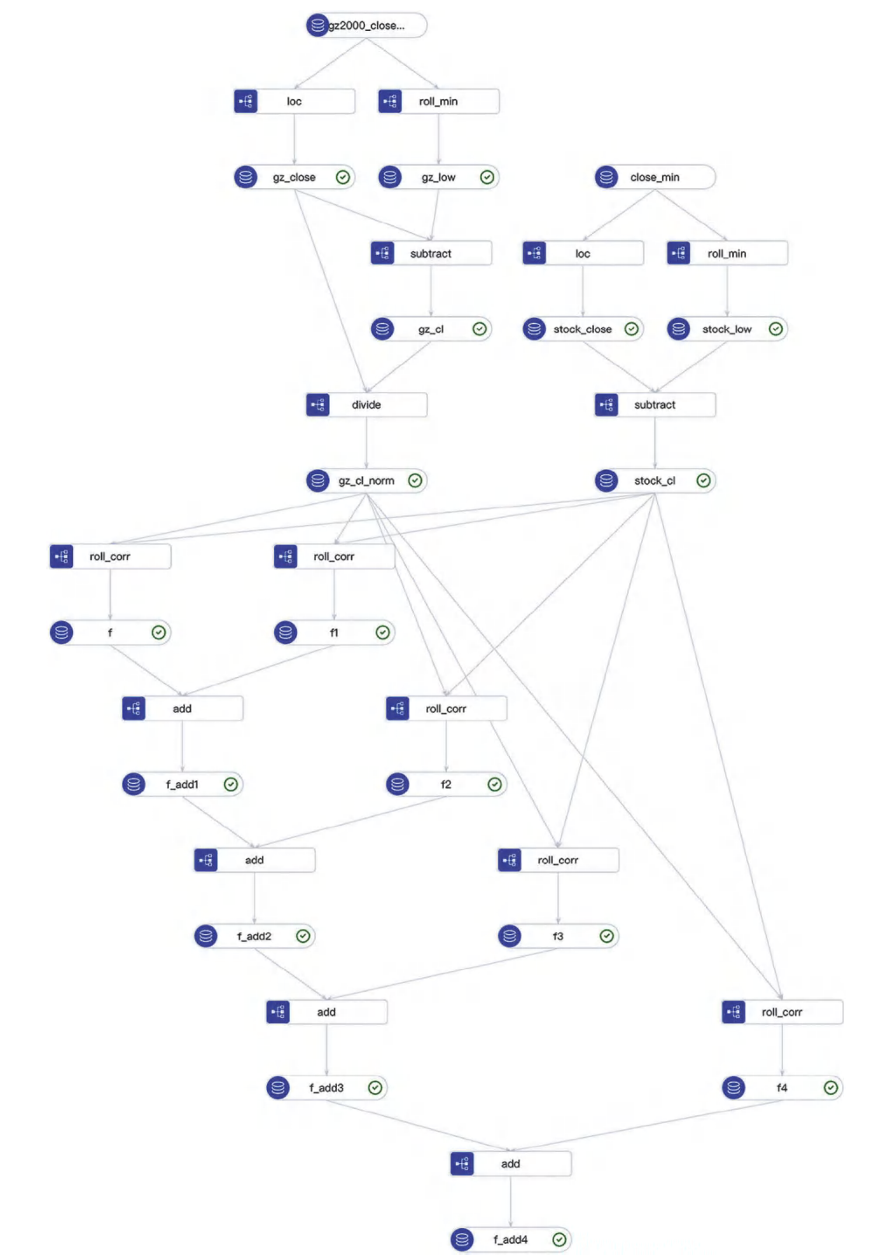
圖12.2 自動化符號化因子

實現因子自動搜索需要以下組件：

1. 操作數空間：用于因子挖掘的元因子，如價格、成交量、行業分類、限價訂單簿特征、分析師/財報統計數據、投資者情緒信號等。
   • 該空間應豐富包含反映股票內在屬性的變量（如前面章節討論）。
   • 理論上更廣闊、更高維的操作數空間能提供更有意義邏輯發現的可能性。
2. 操作符空間：用于處理因子的操作符，如平方根、對數、排序、均值、分位數等，以及后處理操作符（如離群值裁剪的縮尾處理和數據標準化）。
   • 與操作數空間類似，多樣化的操作符集合能增強搜索能力。
3. 搜索算法：旨在發現有效因子，方法包括隨機組合的蒙特卡洛(MC)算法，更復雜的馬爾可夫鏈蒙特卡洛(MCMC)和遺傳編程等。
   • 最新研究探索使用生成模型和LangChain基于金融邏輯提出操作數和操作符組合。
4. 評估：簡單標準包括信息系數(IC)、年化收益和夏普比率。
   • 為避免高相關性因子冗余，可采用數據驅動的解釋算法增強搜索因子的邏輯連貫性。
5. 迭代：研究者需持續理解生成結果，識別系統缺陷，并根據結果調整搜索算法或擴展操作數和操作符。
   • 迭代改進對建立功能性因子發現系統至關重要。

Cheng和Tang(2024)研究了GPT-4生成因子的能力。
研究表明：ChatGPT利用GPT-4能力生成的因子在收益和風險方面表現優異，展現出可觀的夏普比率和超越傳統因子模型的年化收益軌跡。通過模型平均范式，ChatGPT生成的35個因子集合顯示出卓越的多空年化收益和顯著夏普比率，優于傳統數據挖掘技術。
GPT-4因子生成過程的突出優勢是時間效率——不同于依賴大量數據挖掘的傳統方法，GPT-4基于知識的推理允許無需大量金融數據即可快速生成因子。重要的是ChatGPT提供基于經濟理論的生成因子全面解析，這區別于純數據挖掘方法，增強了因子的可解釋性和穩健性。
該研究凸顯了ChatGPT等大型語言模型(LLM)在因子生成中日益增長的相關性。

金融市場收益預測傳統依賴詞袋法，無法捕捉文本句法和語義。而自然語言處理領域最先進的LLM提供的語境化表征能更全面理解新聞文本。Chen等(2024)探索使用16個國家股票市場和13種語言新聞數據，研究語境化表征在收益預測中的功效。這些表征捕獲文本的語境信息和細微差別，克服了詞袋法的局限（尤其涉及否定詞的情況）。研究發現，新聞信息以非有效延遲方式納入股價，但利用實時新聞提醒的交易策略能利用新聞誘導的收益可預測性，產生了更高夏普比率。

關于因子可解釋性，Guo等(2023)的方法包括：

1. 股票解釋：提供股票與其他股票關系、股票相似性、領先-滯后效應和行業趨勢的洞見，有助于更好理解其行為及在分析和預測中相比傳統方法的潛在優勢。但確定適當相似性指標、識別領先-滯后效應及評估行業貢獻和特征交互等方面存在挑戰。
2. 時間解釋：提供特定時點市場特征和異常的洞察，包括極端市場狀況、日歷效應、風格轉換和突發事件影響。通過分解收益、識別重要日歷因子、檢測風格轉換和分析事件影響，投資者可調整策略以應對市場動態。
3. 因子解釋：分析股票對不同因子隨時間變化的敏感性，識別因子間交互效應。因子可根據數據源、金融特征和時間尺度等多方面分類，計算其對組合收益的貢獻。通過特征交叉技術揭示因子交互作用，使用層次聚類等技術創建因子相似性的層次化描述。

這種利用AI算法進行因子研究的多維方法，強調了將先進技術整合到因子投資的復雜性和潛力，凸顯了在這一演進領域持續探索和完善的重要性。

12.5 機器學習 vs. 計量經濟學

毫無疑問，機器學習已逐漸取代計量經濟學方法，成為當代資產定價和因子投資的主導工具。但在結束本章前，從統計建模視角檢視這兩種方法的差異頗具啟發性（Mullainathan和Spiess 2017, Athey和Imbens 2019）。這種比較能加深我們對方法論的理解，從而為手頭問題選擇合適技術。

12.5.1 兩種文化

• Leo Breiman在其開創性論文《統計建模：兩種文化》（Breiman 2001）中深入探討統計建模的兩種主流文化。
  • 第一種是數據建模文化，假設數據生成過程基于某個隨機模型，并據此進行統計推斷。
    • 其主要目標是理解數據結構和內部關系，即傳統數據建模文化的本質在于通過一系列假設和理論框架理解數據生成機制。
    • 該文化中廣為人知的計量經濟學方法，依賴建立顯式模型解釋變量間關系，通常假設線性關系和誤差正態分布。
    • 該方法主要目標是參數估計而非預測，旨在闡明變量間因果關系。
      • 當數據符合模型假設時，該方法可提供強有力的因果解釋。時間序列回歸或Fama和MacBeth(1973)橫截面回歸等實證研究方法都屬于這一文化。
      • 但當預測精度優先于無偏參數估計時，會發生什么？
  • 第二種是算法建模文化，優先考慮預測精度而非模型可解釋性。
    • 該方法不對數據生成過程做嚴格結構假設，而是采用數據驅動方法直接從數據中學習。
    • 機器學習模型是這一文化的典型代表。其靈活性使其能處理復雜、非線性和高維數據，無需預設數據結構。
      • 但機器學習模型常因"黑箱"特性受到批評。
    • 該文化中不對數據結構做任何假設，而是選擇一類模型（如神經網絡）并根據給定損失函數從數據中學習模型參數。
    • 機器學習建模核心是優化模型樣本外泛化性能，或等價于最小化泛化誤差，由此引入正則化這一關鍵概念。
    • 相比計量經濟學，機器學習方法無需明確定義模型形式即可逼近非線性、高維和復雜函數關系，使其自然適合解決當代實證資產定價挑戰。
• 通過這兩種文化視角觀察計量經濟學與機器學習，它們的差異顯而易見。如Breiman(2001)強調：傳統統計方法與機器學習的根本分歧在于，
  • 前者在已知數據模型假設下聚焦參數估計和統計檢驗，
  • 而后者在不假設已知數據模型情況下最大化預測精度。
• 換言之，
  • 對計量經濟學，參數估計先于預測精度；
  • 對機器學習，預測精度先于參數估計。
• 若考慮資產定價實證研究目標，
  • 計量經濟學主要關注定價模型能否在樣本內定價測試資產，
  • 而機器學習聚焦基于模型預測構建的組合能否在樣本外實現最優風險調整收益。

12.5.2 機器學習與計量經濟學的協同

在資產定價和因子投資領域，兩種文化不應被視為對立力量，而應作為互補方法（Kelly和Xiu 2023）。計量經濟學原理與機器學習預測能力的融合，可豐富我們的理解并提升投資策略效力。

例如，將計量經濟學的因果檢驗納入機器學習流程，有助于識別&驗證背后有真實經濟邏輯的預測因子，從而降低偽相關風險。
此外，計量經濟學強調理解底層DGP可指導機器學習模型的特征選擇，確保輸入變量不僅是統計假象。這種綜合方法也能促進機器學習模型的可解釋性。例如，模型無關的可解釋性工具可應用于機器學習模型，闡明輸入特征與預測間關系，從而提供類似計量經濟學模型的洞見（Ribeiro、Singh和Guestrin 2016）。
再者，計量經濟學對不確定性和推斷的嚴謹處理能增強機器學習在金融中的應用。例如，研究機器學習模型預測的漸近分布，能讓投資者更細致地理解模型生成預測信號的風險和可靠性。

反過來，機器學習能揭示傳統計量經濟學方法可能忽略的新實證規律，從而豐富經濟學和金融學的假設檢驗與理論發展。機器學習的數據驅動特性使其能發現金融數據中復雜的非線性模式和交互作用，這些可能并非立即顯現或理論預期。例如，機器學習技術能識別大量市場指標和經濟信號間錯綜復雜的關系，揭示資產收益或經濟周期此前未被認識的預測因子。

總之，計量經濟學嚴謹性與機器學習靈活性間的相互作用，為推進資產定價和因子投資提供了肥沃土壤。通過結合兩種方法的優勢——計量經濟學對因果性、可解釋性和嚴格推斷的關注，與機器學習處理復雜非線性關系和大數據的能力——金融界能開發更穩健、深刻和有效的因子。這種互補協同凸顯了金融研究中多學科視角的必要性，既要擁抱計量經濟學的豐富傳統，也要接納機器學習的創新潛力（Varian 2014）。

12.6 結論

總結本章，我們反思了機器學習在資產定價和因子投資領域的變革性作用。機器學習算法與該領域的整合不僅增強了研究者和實踐者的分析能力，更開啟了金融建模與預測的新紀元。

本章同時強調了融合計量經濟學理論與機器學習自適應能力的協同方法的重要性。這種多學科策略確保了我們開發的模型不僅預測能力強，而且立足經濟原理并具可解釋性。面對不斷演進的市場動態，保持模型可信度與相關性需依賴這種平衡。

展望未來，機器學習在因子投資中的潛力看似無限。但這一征程并非沒有挑戰。過擬合、可解釋性和穩健驗證框架需求等問題仍是我們考量的重點。未來的征程無疑需要學界與業界的協同努力以有效應對這些挑戰。隨著我們持續探索這一激動人心的前沿領域，計量經濟學智慧與機器學習創新的融合，有望在復雜的金融世界中釋放更深刻的洞見并創造更有效的投資策略。