前言

依舊是只會寫簽到題的一場。

---

A.約數個數和

題目傳送門：約數個數和

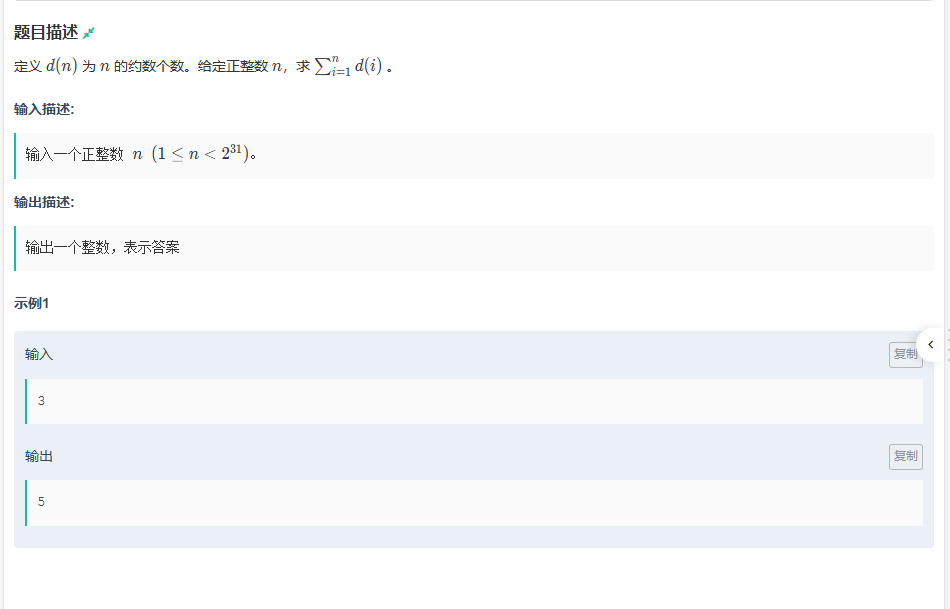
這一題利用到了整除分塊，如果不這樣的話，數據太大，會時間超限。
AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll ans=0;
void solve()
{ll n;cin>>n;for(ll l=1,r;l<=n;l=r+1){r=n/(n/l);ans+=(n/l)*(r-l+1);}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;}

整除分塊(相當于約數求和)

介紹：整除分塊（也叫數論分塊）是數論和算法競賽中常用的優化技巧，主要用于高效計算形如
$$\sum _{i=1}^{n}f(i)?g\left(?\frac{n}{i}?\right)$$ 的求和式，核心思想是利用「整除的周期性」，將求和式中結果相同的區間合并，減少計算次數。
一、整除分塊的核心原理：
利用整除的「周期性」對于固定的 n，當 i 從 1 到 n 變化時，$$?\frac{n}{i}?$$ 的值會分段相同。
例如：(n=10) 時，$$?\frac{10}{i}?$$ 的取值如下：

可以看到，$$?\frac{n}{i}?$$ 的值會形成連續的區間段（如 i=4,5 時，值都是 2；$$i=6～10$$時，值都是 1）。關鍵發現：
對于某個值 $$k=?\frac{n}{i}?$$，所有能使 $$?\frac{n}{i}?=k$$的 i 會構成一個連續區間 ([l, r])，其中：左端點 l 是當前區間的起始右端點 r 滿足：
$$r=?\frac{n}{k}?=?\frac{n}{?\frac{n}{l}?}?$$
利用這一性質，我們可以將原本需要遍歷 n 次的求和，優化為遍歷所有不同的 k 對應的區間段，$$時間復雜度從O(n)降到O(\sqrt{n})（因為不同的k最多有2\sqrt{n}個）$$。
模板：

long long sum = 0;
for (int l = 1, r; l <= n; l = r + 1) {int k = n / l;r = n / k;  // 計算當前段的右端點sum += (r - l + 1) * k;
}

相關例題：取模

題目傳送門：取模



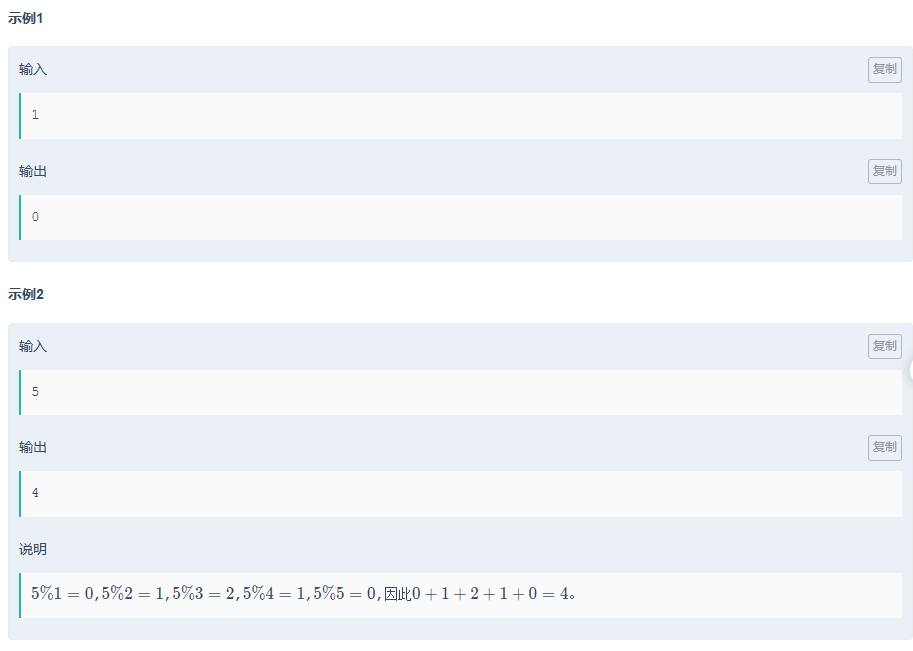
對于這一題，同樣可以通過一系列推理，將其轉換到整除分塊
利用取模的數學定義：
$$n\%i=n?i??\frac{n}{i}?$$因此，原求和式可展開為：
$$\sum _{i=1}^n\left(n\%i\right)=\sum _{i=1}^n\left(n?i??\frac{n}{i}?\right)$$拆分求和式：
$$\sum _{i=1}^n\left(n\%i\right)=\sum _{i=1}^{n}n?\sum _{i=1}^n\left(i??\frac{n}{i}?\right)$$
對于i求和，可以通過等差數列求和推理出來
AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
const ll mod=998244353;
void solve()
{ll n;cin>>n;__int128 ans=0;//特別注意類型，因為數據范圍非常大for(__int128 l=1,r;l<=n;l=r+1){ll k=n/l;r=n/k;ans+=k*((r-l+1)*(r-l)/2+(r-l+1)*l)%mod;}ll an=((__int128)n*(__int128)n-ans)%mod;cout<<an<<endl;
}
signed main()
{IOS;ll t=1;// cin>>t;while(t--)solve();return 0;
}

B.異或期望的秘密

題目傳送門：異或期望的秘密

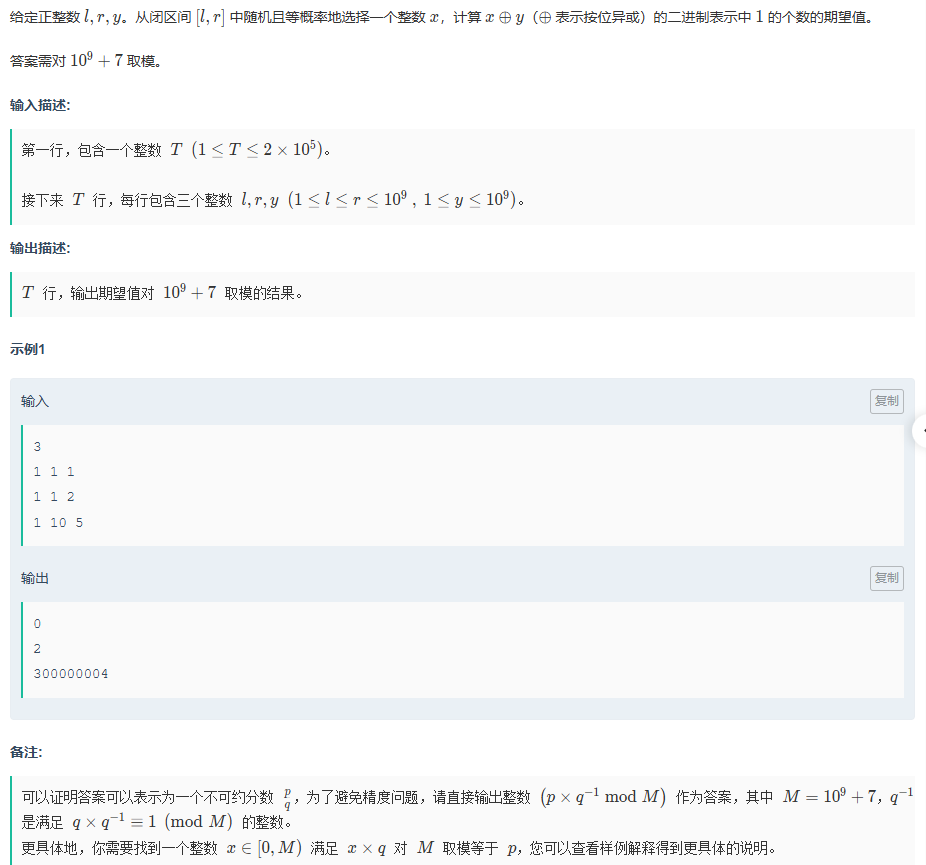
這一題用到的知識就很多了，有關于二進制的規律，以及乘法逆元，還有數學期望的計算；
思路：
通過數據范圍可以發現，直接進行循環肯定會時間超限，為此就有了一個很妙的方法，利用到異或以及二進制的規律，通過遍歷y在bitset的每一位，通過當前y在二進制下的0與1，與L到R之間相同位數下的1的個數來進行判斷，由于異或的性質，相同為0，由此來反著推出貢獻為1的總數，最后再通過乘法逆元。
AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
const ll mod=1e9+7;
ll qmod(ll x,ll y)//乘法逆元（快速冪）
{ll sum=1;while(y){if(y&1){sum*=x;sum%=mod;}x*=x;x%=mod;y>>=1;}return sum;
}
ll f(ll x,ll i)//計算x第i位的1的個數
{if(x==0)return 0;ll sum=0;ll val=1ll<<i;//每個周期的貢獻值ll curr=1ll<<(i+1);//一個周期的大小ll re=x%curr-val+1;//計算不足一個周期的貢獻值sum+=val*(x/curr);//計算整周期的貢獻sum+= max((ll)0,re);//比較剩余周期是否有貢獻值sum%=mod;return sum;
}
void solve()
{ll l,r,y;cin>>l>>r>>y;ll k=r-l+1;ll ans=0;bitset<31>m(y);//方便進行異或for(ll i=0;i<=29;i++){ll num=f(r,i)-f(l-1,i);//計算當前位數的區間1的個數總和if(m[i]==1)num=k-num;//貢獻為0的反推出貢獻為1的ans+=num;ans%=mod;}cout<<(ans*qmod(k,mod-2))%mod<<endl;//乘法逆元
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)solve();return 0;
}

二進制的規律

1 —— 00001
2 —— 00010
3 —— 00011
4 —— 00100
5 —— 00101
6 —— 00110
7 —— 00111
8 —— 01000
9 —— 01001
10 ——01010
11 —— 01011
12 —— 01100
13 —— 01101
14 —— 01110
15 —— 01111
16 —— 10000
17 —— 10001
18 —— 10010
19 —— 10011
20 —— 10100
通過觀察會發現，每一位的周期就是權值的2倍，而權值又是該當前位數的
(2ⁱ ),注意位數i是從0開始的，故而周期為2ⁱ⁺¹ .
至于求余數的貢獻值時，會發現在周期的一半的前一位值是1，故而需要多加上1，因為其是余數減去一半的周期。
關鍵點：

    if(x==0)return 0;ll sum=0;ll val=1ll<<i;//每個周期的貢獻值ll curr=1ll<<(i+1);//一個周期的大小ll re=x%curr-val+1;//計算不足一個周期的貢獻值sum+=val*(x/curr);//計算整周期的貢獻sum+= max((ll)0,re);//比較剩余周期是否有貢獻值

相關例題

累加器

題目傳送門：累加器


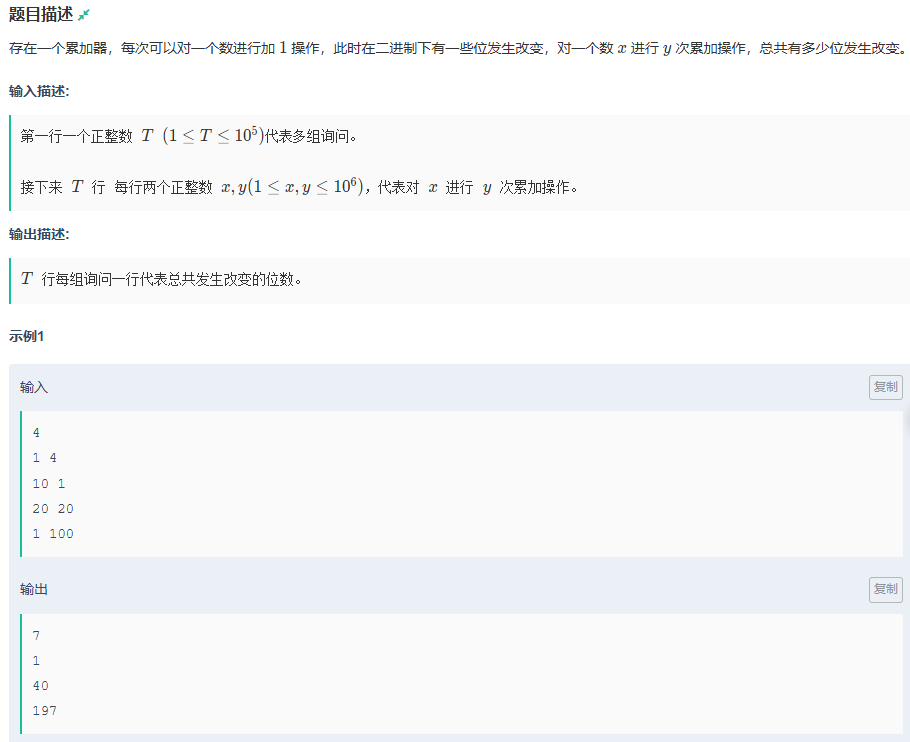
通過觀察樣例會發現，每位改變的位數，都與當前的2的位數次方
AC代碼;

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
const ll N=1e6+10;
ll f(ll x)//進行前綴和
{ll sum=0;ll y=log2(x);for(ll i=0;i<y;i++){ll k=(ll)pow(2,i);//關鍵規律sum+=x/k;}return sum;
}
void solve()
{ll x,y;cin>>x>>y;cout<<f(x+y)-f(x)<<endl;
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)solve();return 0;
}

小藍的二進制詢問

題目傳送門：小藍的二進制詢問

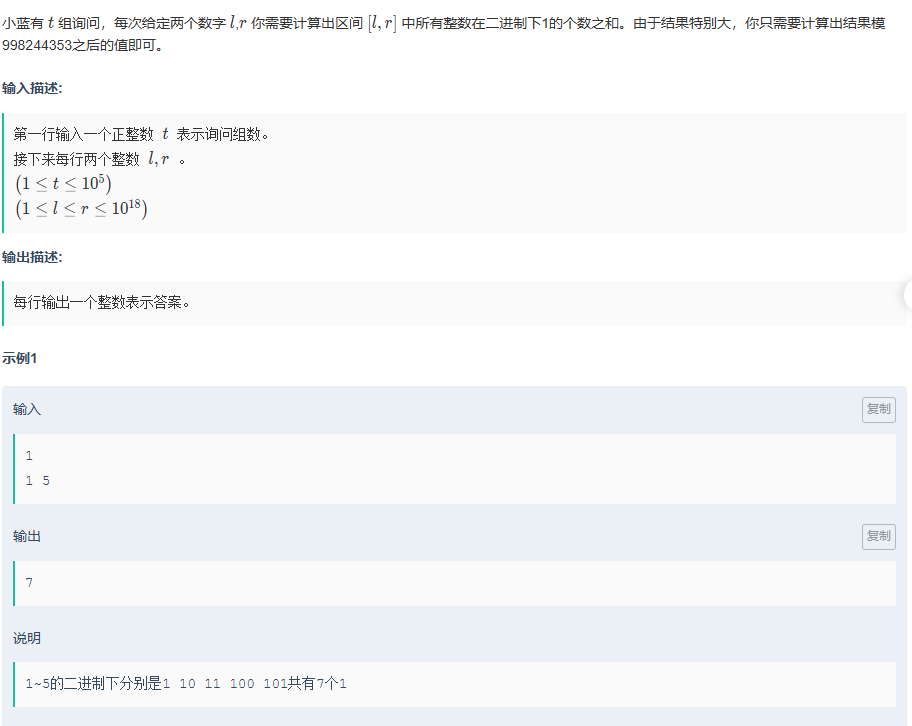
這一題便是之前的規律了；
AC代碼

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
const ll N=1e6+10;
const ll mod=998244353;
ll f(ll x)
{ll sum=0;ll y=log2(x)+1;//計算當前的位數if(x==0)return 0;ll val=1;for(ll i=0;i<=y;i++){val=1ll<<i;//權值ll curr=val*2;//周期sum+=val*(x/curr);//完整周期總和ll re=x%curr-val+1;//剩余周期的貢獻sum+=max((ll)0,re);//判斷是否有貢獻sum%=mod;}return sum%mod;
}
void solve()
{ll x,y;cin>>x>>y;cout<<(f(y)-f(x-1)+mod)%mod<<endl;
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)solve();return 0;
}

乘法逆元

1. 概念

在數學中，乘法逆元是一個與乘法運算相關的重要概念，它描述了兩個數之間的一種特殊關系。簡單來說，對于給定的數 a，如果存在另一個數 b，使得它們的乘積等于乘法單位元（通常是 1），那么 b 就被稱為 a 的乘法逆元。

2.基本定義

設 a 是一個數（或更廣泛的代數結構中的元素），若存在數 b 滿足：$$a\times b=b\times a=1$$
則稱 b 是 a 的乘法逆元，記作 $$b=a^{?1}$$（讀作 “a 的逆”）。這里的 “1” 是乘法單位元，即與任何數相乘都不改變該數的特殊元素（例如整數乘法中，1 就是單位元）。

3.費馬小定理

1.定理內容

若 p 是一個質數，且整數 a 不是 p 的倍數$$（即a與p互質，\gcd (a,p)=1)$$，
則有：$$a^{p?1}\equiv 1(\mathrm{mod}p)$$
符號解釋：$$\equiv (\mathrm{mod}p)表示“模p同余”，即a^{p?1}除以p的余數等于1。$$

2.重要推論

費馬小定理的一個關鍵應用是求模運算中的乘法逆元。
由定理 $$a^{p?1}\equiv 1(\mathrm{mod}p)$$
變形可得：$$a\times a^{p?2}\equiv 1(\mathrm{mod}p)$$
這表明：當 p 是質數且 a 與 p 互質時，$$a^{p?2}\mathrm{mod}p$$
就是 a 模 p 的乘法逆元$$（即a^{?1}\equiv a^{p?2}(\mathrm{mod}p)）$$。

根據費馬小定理，當 p 是質數且 $$\gcd (a,p)=1時$$，
有：$$a^{p?1}\equiv 1(\mathrm{mod}p)$$
將等式左邊因式分解$$（把a^{p?1}拆成a\times a^{p?2}），得到：a\times a^{p?2}\equiv 1(\mathrm{mod}p)$$

D.開羅爾網絡的備用連接方案

題目傳送門：開羅爾網絡的備用連接方案


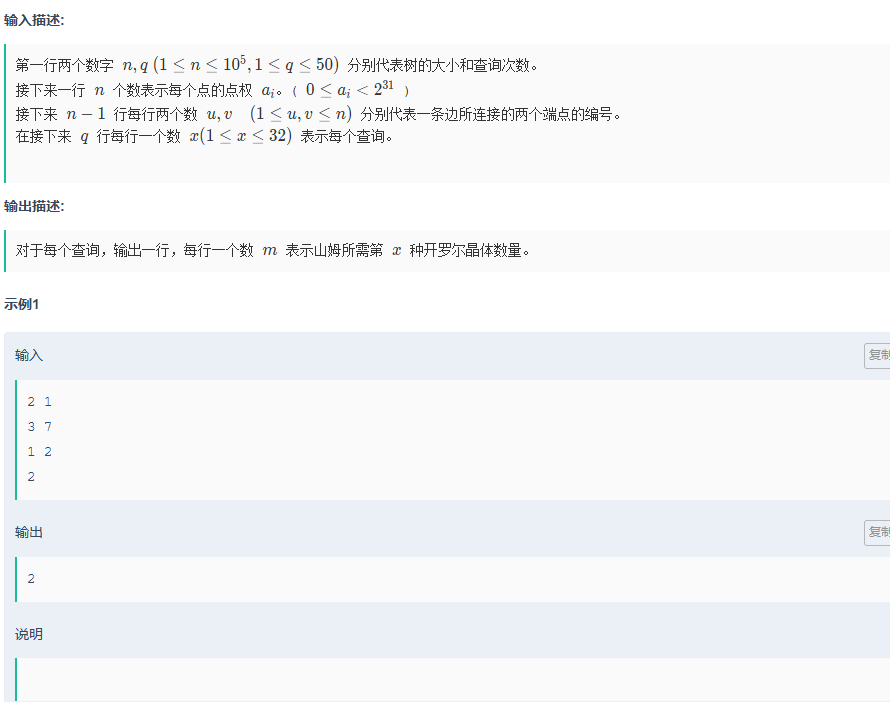
通過題目，可以發現就是一個加權無向圖，來求取經過按位與之后該數二進制下1的個數，

AC代碼

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e5+10;
vector<ll> p[N];//用來存邊
ll a[N];//存該節點的權值
ll ans[N];//保存種類數目
void dfs(ll x,ll w,ll f)
{ll c=a[x]&w;//每次都進行按位與bitset<40>b(c);//為了更好的求1的個數ans[b.count()]++;//統計種類for(ll i:p[x]){if(i!=f)//防止重邊也就是防止一個節點遍歷兩次{dfs(i,c,x);//繼續往下搜索i代表的是子節點，c則是要更新的值，x則代表的是父節點}}
}
void solve()
{ll n,q;cin>>n>>q;for(ll i =1;i<=n;i++)cin>>a[i];for(ll i=1;i<n;i++){ll x,y;cin>>x>>y;p[x].push_back(y);//存邊，即雙向邊p[y].push_back(x);}dfs(1,-1,0);//從節點1開始進行搜索while(q--){ll x;cin>>x;cout<<ans[x]<<endl;}
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;
}

E.咕咕嘎嘎!!!(easy)

題目傳送門：咕咕嘎嘎!!!(easy)


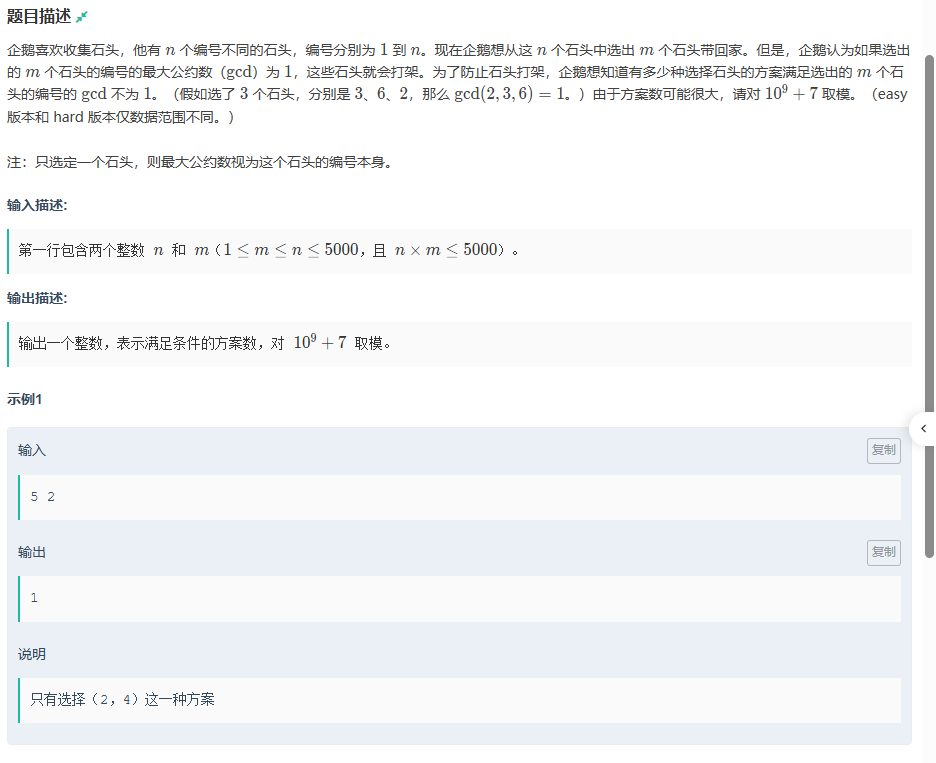
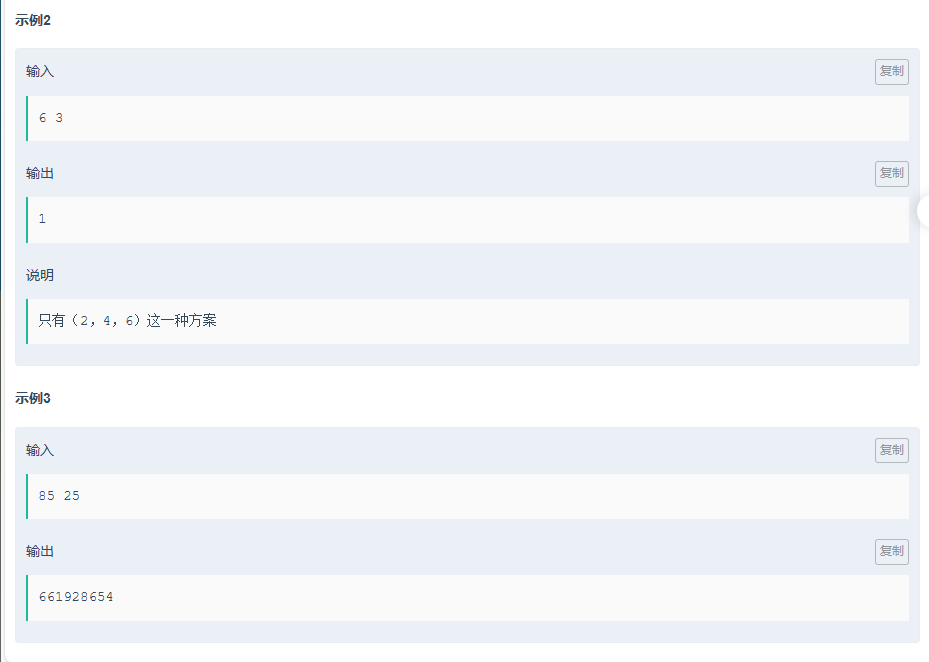
對于這一題，既然最大公因數為1的不滿足，那就求出最大公因數大于等于2的。

一、問題轉化：補集思想 + 容斥原理
題目要求 選 m 個石頭，且它們的 gcd 不為 1 的方案數。直接計算較復雜，采用 補集思想 + 容斥原理 轉化問題：
補集思想
總合法方案 = 所有 gcd 為 d（d≥2）的方案數之和。
但直接枚舉 d 會重復計算（比如 gcd 為 6 的方案會被 d=2 和 d=3 重復統計），因此需要容斥：從大到小枚舉 d，減去其倍數的貢獻。
容斥原理
定義 f[d] 為選 m 個石頭、且它們的 gcd 恰好為 d 的方案數。
但直接求 f[d] 困難，因此先定義 g[d] 為選 m 個石頭、且它們的 gcd 是 d 的倍數（即所有選中的數都是 d 的倍數）的方案數。
則根據容斥關系：$$f[d]=g[d]?\sum _{k>d,d|k}f[k]$$
通過從大到小枚舉 d，用 f[d] -= f[k] 的方式實現容斥。
二，預處理：求組合數
遞推：s[i][j] = s[i-1][j-1] + s[i-1][j]（選第 i 個元素則從 i-1 選 j-1，不選則從 i-1 選 j）。
這樣可以在 O(n^2) 時間內預處理出所有需要的組合數，避免重復計算。
三，核心流程
1. 計算 g[d]：選 m 個 d 的倍數的方案數
對于每個 d（從 1 到 n）：
統計 1~n 中是 d 的倍數的數的個數，記為 num = n / d（因為 d, 2d, 3d, …, kd ≤n → k = n/d）。
若 num ≥ m，則從 num 個數中選 m 個的方案數為組合數 s[num][m]，即 g[d] = s[num][m]；否則 g[d] = 0（不夠選 m 個）。

for(ll i=1;i<=n;i++){ll num=n/i;if(num>=m)f[i]=s[num][m];elsef[i]=0;}

2. 容斥修正：從大到小枚舉 d
為了得到恰好 gcd 為 d 的方案數 f[d]，需要減去所有 d 的倍數 k=2d, 3d, … 的 f[k]：

for(ll i=n;i>=2;i--) {for(ll j=2*i;j<=n;j+=i) {f[i] = (f[i] - f[j] + mod) % mod;}ans = (ans + f[i] + mod) % mod;
}

從大到小枚舉：保證處理 d 時，其倍數 k>d 已經被處理過，這樣減去的 f[k] 是 “恰好 gcd 為 k” 的方案數，避免重復計算。
(f[i] - f[j] + mod) % mod：防止負數，用 mod 調整。
AC代碼

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=5e3+10;
const ll mod=1e9+7;
ll s[N][N];
ll f[N];
void pre()//預處理組合數
{for(ll i=0;i<=N;i++){s[i][0]=0;s[i][i]=1;for(ll j=0;j<i;j++){s[i][j]=(s[i-1][j-1]+s[i-1][j]+mod)%mod;}}
}
void slove()
{ll n,m;cin>>n>>m;ll ans=0;for(ll i=1;i<=n;i++){ll num=n/i;//1~n中i的倍數的個數if(num>=m)// 若數量足夠選m個f[i]=s[num][m];elsef[i]=0;}// 第二步：容斥原理計算f[d] = 選m個數且gcd恰好為d的方案數// 從大到小枚舉d，確保處理d時其倍數已被處理for(ll i=n;i>=2;i--){// 減去所有i的倍數的f[j]（這些是gcd為j的方案，已被包含在g[i]中）for(ll j=2*i;j<=n;j+=i){f[i]=(f[i]-f[j]+mod)%mod;}// 累加所有gcd≥2的方案數ans=(ans+f[i]+mod)%mod;}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;pre();// cin>>t;while(t--)slove();return 0;
}

I.猜數游戲(easy)

題目傳送門：猜數游戲(easy)

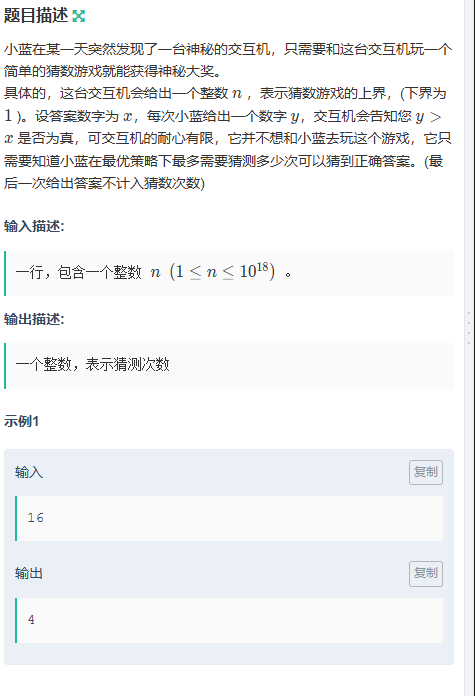
簽到題沒啥說的
AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll ans=0;
void solve()
{ll n;cin>>n;ll sum=1;while(sum<=n){sum*=2;ans++;}if(sum/2==n)cout<<ans-1<<endl;elsecout<<ans<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;}

K.打瓦

題目傳送門：打瓦

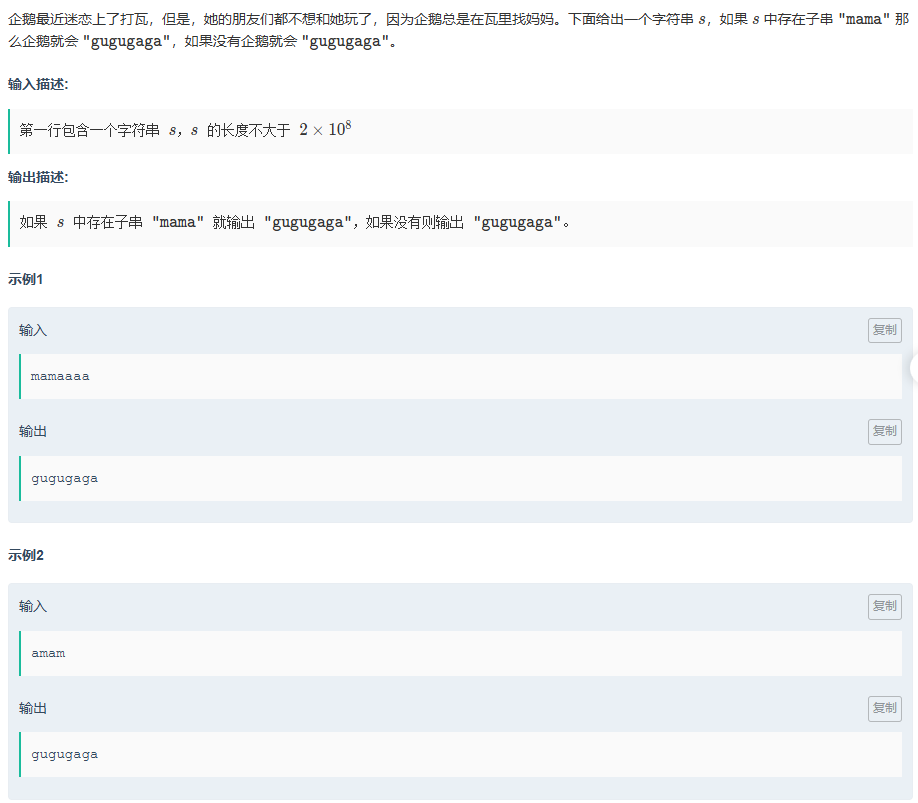
同樣簽到題
AC代碼

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
void solve()
{string s;cin>>s;cout<<"gugugaga"<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;}

M.米婭逃離斷頭臺

題目傳送門：米婭逃離斷頭臺


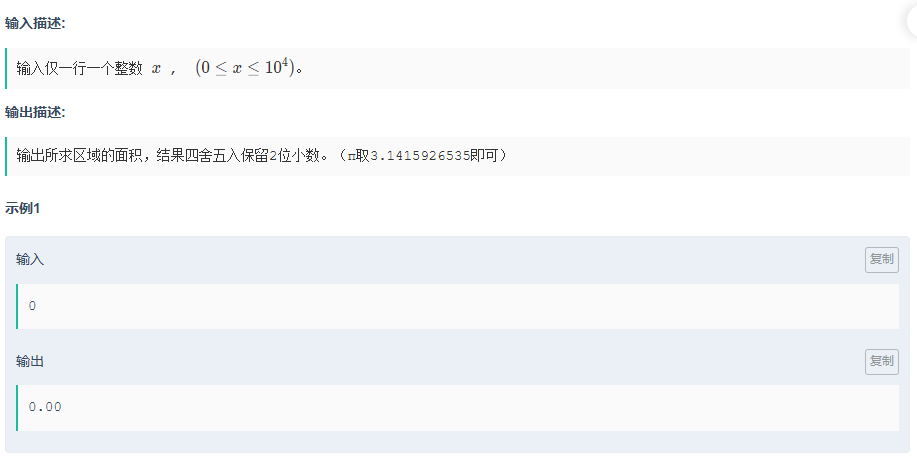
簡單的數學題
AC代碼

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
double x;
void solve()
{cin>>x;double sum=3.1415926535;double ans=0;if(x==0){printf("0.00\n");return ;}else{ans=(sum*x*x)/8;printf("%.2lf\n",ans);}
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)solve();return 0;}

總結

對于其他題，尤其a題就是屬于沒思路的一題
而D題，才開始題目沒看太懂，沒有建立無向邊，建立的是有向邊，等到后續給了題目更近一步的解釋時，越來越迷糊，圖論還是接觸的少。