BitDistiller：通過自蒸餾釋放 Sub-4-Bit 大語言模型的潛力

溫馨提示：
本篇文章已同步至"AI專題精講" BitDistiller：通過自蒸餾釋放 Sub-4-Bit 大語言模型的潛力

摘要

大語言模型（LLMs）的規模不斷擴大，在自然語言處理方面取得了令人矚目的進展，但這也帶來了顯著的部署挑戰。權重量化已成為廣泛采用的解決方案，用于降低內存和計算需求。本文提出了 BitDistiller，一個融合了量化感知訓練（Quantization-Aware Training, QAT）與知識蒸餾（Knowledge Distillation, KD）的框架，用以提升超低精度（sub-4-bit）LLMs 的性能。具體而言，BitDistiller 首先引入了一個定制的非對稱量化與裁剪技術，以最大程度地保留量化權重的精度；隨后提出了一種新穎的置信感知 Kullback-Leibler 散度（Confidence-Aware Kullback-Leibler Divergence, CAKLD）目標函數，并以自蒸餾的方式應用于訓練過程中，從而實現更快的收斂速度和更優的模型性能。實驗結果表明，BitDistiller 在3-bit和2-bit配置下，在通用語言理解和復雜推理任務中均顯著優于現有方法。值得注意的是，BitDistiller 在資源效率方面也更具優勢，所需的數據和訓練資源更少。代碼開源于：https://github.com/DD-DuDa/BitDistiller。

1 引言

擴大模型規模是大語言模型（LLMs）取得成功的關鍵因素，使其在多種自然語言處理任務中展現出前所未有的性能（Brown et al., 2020；Touvron et al., 2023；Kaplan et al., 2020）。然而，模型規模的不斷增長也帶來了部署方面的重大挑戰，尤其是在資源受限的設備上，由于模型的內存占用和計算需求極為龐大。

權重量化作為一種提高 LLM 效率和可部署性的常用策略，能夠在盡量不犧牲性能的前提下大幅壓縮模型體積（Gholami et al., 2022）。在實際應用中，4-bit 量化因其在壓縮比與性能保留之間的良好平衡，被廣泛采用（Lin et al., 2023；Frantar et al., 2022；Liu et al., 2023a）。
在這里插入圖片描述

然而，sub-4-bit 量化會顯著降低模型權重的保真度，進而導致模型性能下降，尤其是在小模型或需要復雜推理的任務中更為明顯（Dettmers 和 Zettlemoyer，2023）。為應對這一問題，研究者提出了多種后訓練量化（Post-Training Quantization, PTQ）和量化感知訓練（Quantization-Aware Training, QAT）方法（Chee 等，2023；Shao 等，2023）。PTQ 的優勢在于無需重新訓練模型，但在極低比特精度下很難維持模型性能。相比之下，QAT 將量化過程融入訓練環節，使模型能動態適應精度降低，從而更好地保留精度（Liu 等，2023b；Kim 等，2023a）。盡管早期成果令人鼓舞，但要在極低比特的 QAT 場景中實現優異的模型性能，仍需解決兩個核心難題：如何在量化中最大限度保留權重精度，以及如何在訓練中有效學習低比特表示。

在本文中，我們提出了 BitDistiller —— 一個將 QAT 與知識蒸餾（Knowledge Distillation, KD）有機融合的新型框架，旨在顯著提升 sub-4-bit 量化 LLM 的性能。為盡量減少量化誤差，BitDistiller 采用了定制的非對稱量化與裁剪策略，以盡可能保留全精度模型的能力，尤其是在超低比特設定下。為了有效且高效地學習低比特表示，BitDistiller 采用了一種簡潔而高效的自蒸餾機制，即使用全精度模型作為教師模型，引導低比特學生模型的訓練。值得一提的是，BitDistiller 創新性地引入了置信感知 Kullback-Leibler 散度（Confidence-Aware Kullback-Leibler Divergence, CAKLD）**作為目標函數，從而優化知識遷移效果，實現更快的收斂速度與更佳的模型性能。

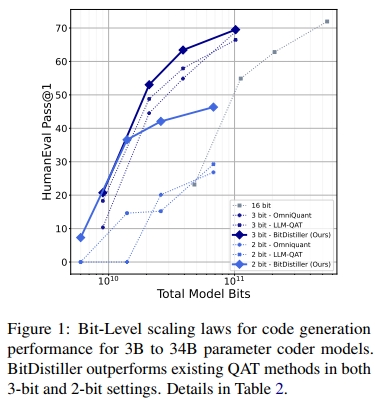
我們在涵蓋通用語言理解、數學推理與代碼生成等多種任務的基準上進行了實證評估，結果表明 BitDistiller 在 sub-4-bit 量化領域顯著優于現有的 PTQ 與 QAT 方法。如圖 1 所示，BitDistiller 在代碼推理基準上，于 3-bit 與 2-bit 配置下均取得了最優的擴展性能表現（scaling law）。此外，BitDistiller 在資源效率方面也表現突出，對訓練數據與資源的需求更低，標志著在資源受限設備上部署強大 LLMs 邁出了重要一步。

2 背景與相關工作

2.1 面向 LLM 的權重量化

PTQ 與 QAT
后訓練量化（Post-Training Quantization, PTQ）直接應用于預訓練模型，無需額外訓練。LLM 的 PTQ 方法通常依賴于誤差調整策略（Frantar 等，2022；Chee 等，2023）或優先保留關鍵權重（Dettmers 等，2023b；Lin 等，2023；Kim 等，2023b）。然而，由于缺乏重新訓練過程，PTQ 在極低比特精度下容易導致模型性能大幅下降。相比之下，量化感知訓練（Quantization-Aware Training, QAT）將量化過程整合到訓練階段，使模型能學習更適用于低比特權重的表示方式。已有的 QAT 方法如 LLM-QAT（Liu 等，2023b）、OmniQuant（Shao 等，2023）、PB-LLM（Shang 等，2023）和 BitNet（Wang 等，2023）在提升模型性能方面已取得顯著成效。盡管如此，QAT 依然面臨對大量訓練數據與資源的高度依賴，仍有較大優化空間。在本研究中，我們結合 QAT 與知識蒸餾（Knowledge Distillation, KD），以增強在 sub-4-bit 場景下量化 LLM 的性能。

量化粒度與格式優化
大量研究表明，采用更細粒度的量化策略（如分組量化）相比于逐層（layer-wise）或通道級（channel-wise）量化方法能獲得更高精度（Shen 等，2020；Frantar 等，2022）。此外，在 LLM 的量化中，浮點數格式（如 FP8、FP4、NF4）被證明比整數格式（如 INT8、INT4）具有更好的精度表現（Kuzmin 等，2022；Dettmers 和 Zettlemoyer，2023；Zhang 等，2023b）。尤其值得注意的是，非對稱量化（asymmetric quantization）在浮點格式中優于對稱量化，因為它能更好地適應模型權重的分布特性（Zhang 等，2023a）。BitDistiller 遵循這些經驗，采用更細粒度的分組方式與非對稱量化策略來提升性能。

2.2 面向 LLM 的知識蒸餾

在大語言模型領域，白盒知識蒸餾（white-box KD）因教師模型的可訪問性而愈發流行，這種方式可以更有效地將教師模型的知識表示傳遞給學生模型（Hinton 等，2015；Zhu 等，2023）。例如，MINILLM（Gu 等，2023）使用反向 KL 散度（KLD）來保證語言生成的準確性與保真性。GKD（Agarwal 等，2023）則探索了更廣義的 Jensen-Shannon 散度（JSD），并通過從學生模型中采樣輸出緩解分布失配的問題。

為了實現極高的壓縮比，將 KD 與模型量化相結合是一種有前景的策略，KD 能有效緩解量化后模型的精度損失（Zhang 等，2020；Kim 等，2022）。在應用 QAT 與 KD 結合的前沿研究中，TSLD（Kim 等，2023a）考慮了過擬合風險，并結合了 logit 蒸餾與真實標簽損失；LLM-QAT 則利用教師模型生成的隨機數據進行無數據蒸餾（data-free distillation）。與 TSLD 和 LLM-QAT 不同，我們的方法在極低比特量化精度下實現了更優的性能表現與更高的資源效率。

3 方法

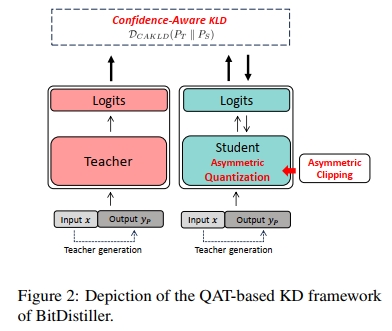
在這里插入圖片描述

在本節中，我們介紹 BitDistiller ——一個面向大語言模型（LLMs）的量化感知訓練（QAT）與自蒸餾框架，如圖 2 所示。為了在量化過程中最大程度地保留權重的保真性，我們首先提出一種非對稱量化與截斷方法（見第 3.1 節）。其次，為了抵消因精度降低而帶來的性能下降，我們引入知識蒸餾（Knowledge Distillation），并提出一種新的置信度感知 KL 散度（Confidence-Aware KL Divergence，CAKLD）作為目標函數，在該目標中，全精度模型作為教師模型，而低精度模型則作為學生模型（見第 3.2 節）。

算法 1 概述了 BitDistiller 的整體流程。給定全精度權重 ww，BitDistiller 首先對 ww 應用非對稱截斷操作，以緩解異常值的影響（第 1 行），該步驟在訓練循環之前進行。隨后，在每一個訓練步驟中，BitDistiller 使用量化后的權重 wQtw_{Qt} 進行前向傳播（forward），并通過所提出的 CAKLD 損失函數 計算損失值（第 4-5 行），然后更新全精度權重（第 6-7 行）（Bengio 等人，2013）。當訓練結束后，BitDistiller 輸出最終的量化權重。

3.1 非對稱量化與截斷

在大語言模型（LLMs）的權重量化中，采用更細粒度（即更小的分組規模）通常會導致權重分組呈現非對稱分布，并且伴隨離群值的出現。在低比特的后訓練量化（PTQ）場景中，若要維持模型性能，恰當處理這種非對稱性是至關重要的。

我們的研究發現：在極低比特的量化感知訓練（QAT）中（如 3 比特和 2 比特配置），非對稱性帶來的影響更為顯著，因此需要定制的策略加以應對。

因此，在 BitDistiller 中，我們引入了非對稱量化技術，并結合非對稱截斷策略，以提升量化權重的表達保真度，最大限度地保留全精度模型的能力。
在這里插入圖片描述
非對稱量化
已有研究表明，在 LLM 量化中，浮點格式（如 FP、NF）通常優于整數格式（INT）（Dettmers 等，2023a；Liu 等，2023a）。然而，當量化精度降低至 2-bit 時，我們觀察到 FP/NF 格式的效果明顯下降。FP/NF 格式之所以在高比特位中表現良好，是由于其非均勻分布特性，能夠捕捉更廣泛的數值范圍，這種非均勻分布與 LLM 中權重張量的自然分布更加契合。

但在 2-bit 場景中，由于其僅能表示四個離散值，表示能力受限，導致非均勻分布的優勢無法有效發揮，從而阻礙了每個數值的有效利用。基于以上觀察，我們在 2-bit 以上的量化中采用 NF 格式，而在 2-bit 場景下則改用 INT 格式。

對于 NF 格式（如 NF3），我們采用 AFPQ 方法（Zhang 等，2023a）實現非對稱量化：為正權重 $w\_{pos}$ 和負權重 $w\_{neg}$ 分別設定獨立的縮放因子 $s\_{pos}$ 與 $s\_{neg}$ ，如公式 (1) 所示。
對于 INT 格式（如 INT2），我們則采用傳統的非對稱方法：使用一個單一的縮放因子和一個指定的零點（zero point），如公式 (2) 所示。

$\left\{ \begin{array} { l l } { { \lfloor { \frac { w _ { p o s } } { s _ { p o s } } } \rceil } , } & { { \mathrm { i f ~ } } w > 0 } \\ { { \lfloor { \frac { w _ { n e g } } { s _ { n e g } } } \rceil } , } & { { \mathrm { i f ~ } } w \leq 0 } \end{array} \right. }\quad(1)$

$\cdot } A s y m : Q ( w ) = \lfloor \frac { w - z } { s } \rceil\quad(2)$

非對稱剪枝（Asymmetric Clipping）
剪枝（clipping）是一種通過限制權重數值范圍來提高量化后模型精度的策略，已有研究證實了其在保持量化精度方面的重要作用（Sakr 等，2022；Shao 等，2023）。然而，樸素的剪枝方法通常效果有限，而更先進的剪枝技術又存在高計算成本的問題，不適用于實際的 QAT 訓練過程（Li 等，2019；Jung 等，2019）。

為克服這一難題，我們提出僅在 QAT 初始化階段使用非對稱剪枝策略。在訓練開始之前進行非對稱剪枝，能夠為模型提供良好的初始點，在不引入迭代剪枝優化的高昂成本的前提下，顯著提升最終量化模型的精度。

具體而言，為了在 QAT 初始化中實現非對稱剪枝，我們利用從一小部分校準數據中緩存得到的輸入特征 $X$ ，為模型的每一層自動搜索兩個最優的剪枝閾值 $α\alpha$ 和 $β\beta$ 。這兩個值的目標是最小化量化前后的輸出差異。形式上，我們優化以下目標函數：
$α?,β?=argmin?α,β∣∣Q(wc)X?wX∣∣\alpha ^ { * } , \beta ^ { * } = \operatorname * { a r g m i n } _ { \alpha , \beta } \lvert \lvert Q ( w _ { c } ) X - w X \rvert \rvert$

$wc=Clip(w,α,β){α∈[min_val,0)β∈(0,max_val](3)w_c = \text{Clip}(w, \alpha, \beta) \begin{cases} \alpha \in [\text{min\_val}, 0) \\ \beta \in (0, \text{max\_val}] \end{cases}\quad(3)$

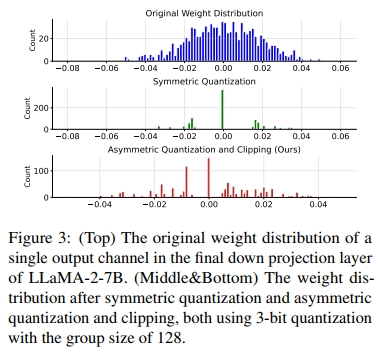
為了展示非對稱量化和裁剪的有效性，我們進行了張量級別的分析。我們從 LLaMa-2-7B 模型中隨機選取了一個權重張量，重點關注其中的一個輸出通道。如圖 3 所示，我們采用的非對稱量化和裁剪方法相比對稱量化能夠更好地保持高保真度。關于非對稱量化和裁剪對模型性能影響的更詳細消融研究，見第 4.4 節的表 3。

在這里插入圖片描述

3.2 帶有 CAKLD 的自我蒸餾

為更好地抵消精度降低帶來的性能下降，我們提出在量化感知訓練（QAT）中采用知識蒸餾（KD），其中全精度模型作為教師，量化后的模型作為學生：

$D(P_T \parallel P_S)\quad(4)$

式中， $D$ 表示兩個分布之間的散度度量， $P_T$ 和 $P_S$ 分別代表全精度模型和量化模型。

知識蒸餾（KD）的直覺可以從兩個方面理解。首先，學習 token 級別的概率分布有助于量化模型更好地模仿其全精度對應模型（Hinton 等，2015），從而重新獲得強大的下游任務性能。其次，鑒于大型語言模型（LLM）的生成特性，利用全精度模型來擴展用于量化感知訓練（QAT）的數據規模變得十分容易。

用于蒸餾的散度度量 $D$ 選擇至關重要。Agarwal 等（2023）發現，反向 KL 散度（即 $D_{KL}(P_S \| P_T)$ ）所倡導的“模式尋求”行為在指令調優（Chung 等，2022）任務中表現優于正向 KL 散度（即 $D_{KL}(P_T \| P_S)$ ），而正向 KL 散度促進“模式覆蓋”，在摘要等通用文本生成任務（Narayan 等，2018）中表現更好。為了給 QAT 提供一種通用方案，我們旨在自動權衡“模式尋求”與“模式覆蓋”的行為，而不是基于對下游任務的經驗理解手動選擇。
在這里插入圖片描述
為此，我們提出了一種新穎的置信感知 KL 散度，簡稱 CAKLD。它通過一個由平均 token 概率估計的系數 $γ$ ，將反向 KL 和正向 KL 混合起來，從而使得“模式尋求”和“模式覆蓋”的行為能夠根據全精度模型對訓練數據的置信度自動權衡：
$DCAKLD(PT∥PS)=γDKL(PS∥PT)+(1?γ)DKL(PT∥PS)D_{\text{CAKLD}}(P_T \parallel P_S) = \gamma D_{KL}(P_S \parallel P_T) + (1 - \gamma) D_{KL}(P_T \parallel P_S)$

$DKL(PT∥PS)=E(x,y)～D[1∣y∣∑i=1∣y∣Ec～PT(?∣x,y<i)[log?PT(c∣x,y<i)PS(c∣x,y<i)]](5)D_{KL}(P_T \parallel P_S) = \mathbb{E}_{(x,y) \sim D} \left[ \frac{1}{|y|} \sum_{i=1}^{|y|} \mathbb{E}_{c \sim P_T(\cdot | x, y_{<i})} \left[ \log \frac{P_T(c | x, y_{<i})}{P_S(c | x, y_{<i})} \right] \right]\quad(5)$

$γ=E(x,y)～D[1∣y∣∑i=1∣y∣PT(yi∣x,y<i)]\gamma = \mathbb{E}_{(x,y) \sim D} \left[ \frac{1}{|y|} \sum_{i=1}^{|y|} P_T(y_i | x, y_{<i}) \right]$

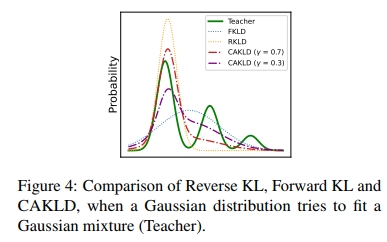
直觀來看，當全精度模型對訓練數據較為自信時，CAKLD 會更傾向于“模式尋求”的行為；反之，當全精度模型對數據不確定時，CAKLD 會更傾向于“模式覆蓋”的行為，因為僅僅建模單一模式并非最優。圖 4 展示了在高斯分布擬合高斯混合分布時，反向 KL 散度、正向 KL 散度與 CAKLD 之間的差異。顯然，CAKLD 能夠通過系數有效權衡“模式尋求”和“模式覆蓋”的行為。有關詳細的性能對比和深入分析，請參見圖 6 及附錄 A.2。

溫馨提示：
閱讀全文請訪問"AI深語解構" BitDistiller：通過自蒸餾釋放 Sub-4-Bit 大語言模型的潛力