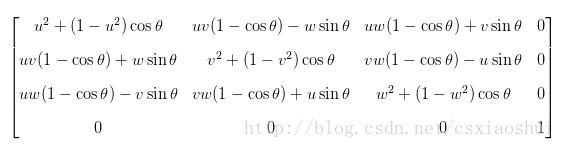1. 簡介
計算機圖形學中的應用非常廣泛的變換是一種稱為仿射變換的特殊變換,在仿射變換中的基本變換包括平移、旋轉、縮放、剪切這幾種。本文以及接下來的幾篇文章重點介紹一下關于旋轉的變換,包括二維旋轉變換、三維旋轉變換以及它的一些表達方式(旋轉矩陣、四元數、歐拉角等)。
2. 繞原點二維旋轉
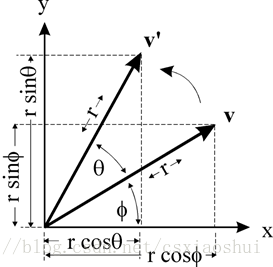
首先要明確旋轉在二維中是繞著某一個點進行旋轉,三維中是繞著某一個軸進行旋轉。二維旋轉中最簡單的場景是繞著坐標原點進行的旋轉,如下圖所示:
如圖所示點v 繞 原點旋轉θθ?角,得到點v’,假設 v點的坐標是(x, y) ,那么可以推導得到 v’點的坐標(x’, y’)(設原點到v的距離是r,原點到v點的向量與x軸的夾角是???)?
x=rcos?y=rsin?x=rcos?y=rsin??
x′=rcos(θ+?)y′=rsin(θ+?)x′=rcos(θ+?)y′=rsin(θ+?)?
通過三角函數展開得到?
x′=rcosθcos??rsinθsin?x′=rcosθcos??rsinθsin??
y′=rsinθcos?+rcosθsin?y′=rsinθcos?+rcosθsin??
帶入x和y表達式得到?
x′=xcosθ?ysinθx′=xcosθ?ysinθ?
y′=xsinθ+ycosθy′=xsinθ+ycosθ?
寫成矩陣的形式是:?
盡管圖示中僅僅表示的是旋轉一個銳角θθ的情形,但是我們推導中使用的是三角函數的基本定義來計算坐標的,因此當旋轉的角度是任意角度(例如大于180度,導致v’點進入到第四象限)結論仍然是成立的。
?
3. 繞任意點的二維旋轉
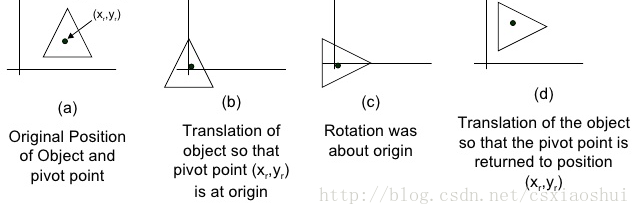
繞原點的旋轉是二維旋轉最基本的情況,當我們需要進行繞任意點旋轉時,我們可以把這種情況轉換到繞原點的旋轉,思路如下:?
1. 首先將旋轉點移動到原點處?
2. 執行如2所描述的繞原點的旋轉?
3. 再將旋轉點移回到原來的位置
也就是說在處理繞任意點旋轉的情況下需要執行兩次平移的操作。假設平移的矩陣是T(x,y),也就是說我們需要得到的坐標 v’=T(x,y)*R*T(-x,-y)(我們使用的是列坐標描述點的坐標,因此是左乘,首先執行T(-x,-y))
在計算機圖形學中,為了統一將平移、旋轉、縮放等用矩陣表示,需要引入齊次坐標。(假設使用2x2的矩陣,是沒有辦法描述平移操作的,只有引入3x3矩陣形式,才能統一描述二維中的平移、旋轉、縮放操作。同理必須使用4x4的矩陣才能統一描述三維的變換)。
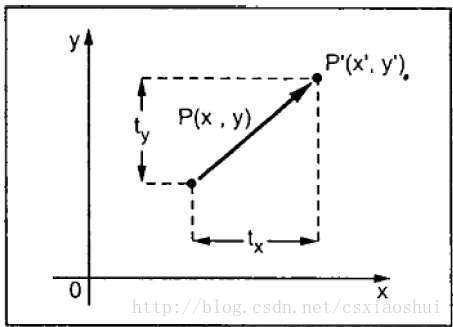
對于二維平移,如下圖所示,P點經過x和y方向的平移到P’點,可以得到:
x′=x+txy′=y+tyx′=x+txy′=y+ty?
由于引入了齊次坐標,在描述二維坐標的時候,使用(x,y,w)的方式(一般w=1),于是可以寫成下面矩陣的形式
?
按矩陣乘法展開,正好得到上面的表達式。也就是說平移矩陣是?
如果平移值是(-tx,-ty)那么很明顯平移矩陣式?
我們可以把2中描述的旋轉矩陣也擴展到3x3的方式,變為:?
從平移和旋轉的矩陣可以看出,3x3矩陣的前2x2部分是和旋轉相關的,第三列與平移相關。有了上面的基礎之后,我們很容易得出二維中繞任意點旋轉的旋轉矩陣了,只需要把三個矩陣乘起來即可:
?
?
?
4. 三維基本旋轉
我們可以把一個旋轉轉換為繞基本坐標軸的旋轉,因此有必要討論一下繞三個坐標值x、y、z的旋轉。?
本文在討論過程中使用的是類似于OpenGL中定義的右手坐標系,同時旋轉角度的正負也遵循右手坐標系的約定。如下圖所示
4.1 繞X軸的旋轉
在三維場景中,當一個點P(x,y,z)繞x軸旋轉θθ角得到點P’(x’,y’,z’)。由于是繞x軸進行的旋轉,因此x坐標保持不變,y和z組成的yoz(o是坐標原點)平面上進行的是一個二維的旋轉,可以參考上圖(y軸類似于二維旋轉中的x軸,z軸類似于二維旋轉中的y軸),于是有:?
x′=xx′=x?
y′=ycosθ?zsinθy′=ycosθ?zsinθ?
z′=ysinθ+zcosθz′=ysinθ+zcosθ?
寫成(4x4)矩陣的形式?
?
4.2 繞Y軸旋轉
繞Y軸的旋轉和繞X軸的旋轉類似,Y坐標保持不變,除Y軸之外,ZOX組成的平面進行一次二維的旋轉(Z軸類似于二維旋轉的X軸,X軸類似于二維旋轉中的Y軸,注意這里是ZOX,而不是XOZ,觀察上圖中右手系的圖片可以很容易了解到這一點),同樣有:?
x′=zsinθ+xcosθx′=zsinθ+xcosθ?
y′=yy′=y?
z′=zcosθ?xsinθz′=zcosθ?xsinθ?
寫成(4x4)矩陣的形式?
?
4.3 繞Z軸旋轉
與上面類似,繞Z軸旋轉,Z坐標保持不變,xoy組成的平面內正好進行一次二維旋轉(和上面討論二維旋轉的情況完全一樣)?
?
4.4 小結
上面描述了三維變換中繞單一軸旋轉的矩陣表達形式,繞三個軸旋轉的矩陣很類似,其中繞y軸旋轉的矩陣與繞x和z軸旋轉的矩陣略有點不同(主要是三個軸向順序和書寫矩陣的方式不一致導致的,繞三個不同坐標旋轉軸以及其他二個坐標軸組成平面的順序是: XYZ(繞x軸) YZX(繞y軸) ZXY(繞z軸),其中繞y軸旋轉,其他兩個軸是ZX,這和我們書寫矩陣按
的方式不一致,而導致看起來繞Y軸旋轉的矩陣似乎是和其他兩個矩陣不一致。如果我們顛倒寫法,將公式寫成?
的方式,那么這三個旋轉矩陣看起來在形式上就統一了,都是?
這種表現形式了(左上角都是?sinθ?sinθ)
?
5. 繞任意軸的三維旋轉
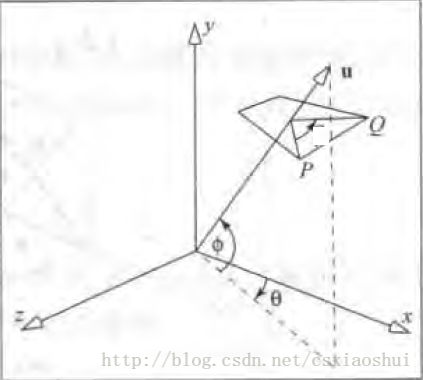
繞任意軸的三維旋轉可以使用類似于繞任意點的二維旋轉一樣,將旋轉分解為一些列基本的旋轉。繞任意軸旋轉如下圖所示:
P點繞向量u旋轉θθ角,得到點Q,已知P點的坐標和向量u,如何求Q點的坐標。?
我們可以把向量u進行一些旋轉,讓它與z軸重合,之后旋轉P到Q就作了一次繞Z軸的三維基本旋轉,之后我們再執行反向的旋轉,將向量u變回到它原來的方向,也就是說需要進行的操作如下:?
1. 將旋轉軸u繞x軸旋轉至xoz平面?
2. 將旋轉軸u繞y軸旋轉至于z軸重合?
3. 繞z軸旋轉θθ角?
4. 執行步驟2的逆過程?
5. 執行步驟1的逆過程?
原始的旋轉軸u如下圖所示:

第1、2、3步驟如下圖所示:?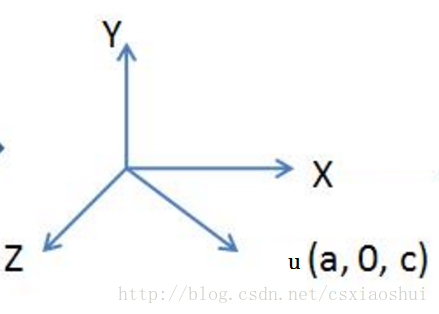
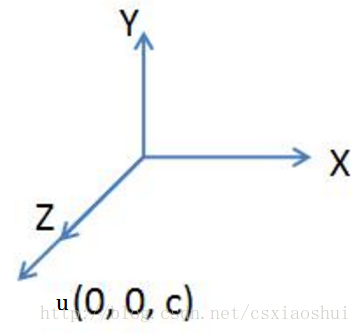
步驟1將向量u旋轉至xoz平面的操作是一個繞x軸的旋轉操作,步驟2將向量u旋轉到與z軸重合,第1、2步驟的示意圖如下:
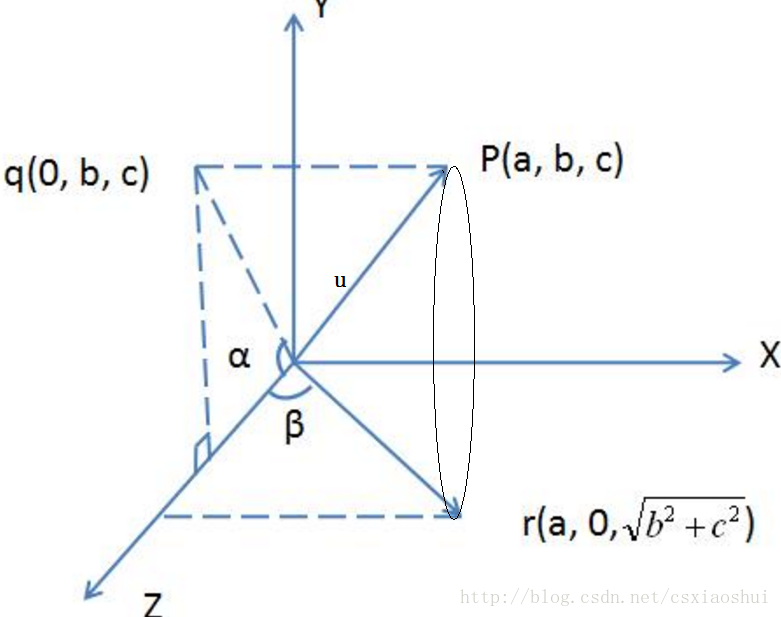
作點P在yoz平面的投影點q,q的坐標是(0, b, c),原點o與q點的連線oq和z軸的夾角就是u繞x軸旋轉的角度。通過這次旋轉使得u向量旋轉到xoz平面(圖中的or向量)【步驟1】?
過r點作z軸的垂線,or與z軸的夾角為ββ, 這個角度就是繞Y軸旋轉的角度,通過這次旋轉使得u向量旋轉到與z軸重合【步驟2】
步驟1中繞x軸旋轉的是一次基本的繞x軸的三維旋轉,按照之前的討論,旋轉矩陣是:?
這里的θθ就是圖中所示的αα角 (注意αα角度是繞x旋轉的正的角度)?
從圖中我們還可以得到:?
于是旋轉矩陣(記作?Rx(α)Rx(α))為:?
在完成步驟1之后,向量u被變換到了r的位置,我們繼續步驟2的操作,繞y軸旋轉負的ββ角(注意:這里的ββ是負的),經過這次變換之后向量u與z軸完全重合,由于這一步也是執行的一次繞Y軸的基本旋轉,旋轉矩陣(記作?Ry(?β)Ry(?β))為:?
使用?β?β替換表達式中的θθ,此外根據圖中描述,我們可以計算得到:?
帶入上面的表達式,于是旋轉矩陣(記作?Ry(?β)Ry(?β))為:?
?
在完成前面兩個步驟之后,u方向和z軸完全重合,因此執行旋轉θθ角,執行的是一次繞z軸的基本三維旋轉(記作?R(θ)R(θ),根據之前的討論,我們可以得到:?
最后兩步驟是前面1和2的逆操作,也就是繞Y軸旋轉ββ?和繞X軸旋轉?α?α,這兩個矩陣分別記作?Ry(β)Ry(β)?和?Rx(?α)Rx(?α),得到它們的方式很簡單,只需要將上面步驟1和步驟2中的角度修改成相反數即可,也就是:
?
?
?
最終得到 繞任意軸u旋轉的旋轉矩陣是【因為使用的列向量,因此執行的是左乘(從右往左)】:
?
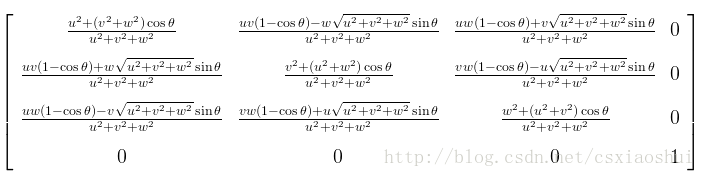
(注:式中的(u,v,w)對應上文中向量(a,b,c),公式我自己筆算過,為了減少編輯公式的時間(使用LaTex編輯太繁瑣,因此找了一張公式的圖片貼在此處)
?
如果向量是經過單位化的(單位向量),那么有a2+b2+c2=1a2+b2+c2=1,可以簡化上述的公式,得到:
參考文獻:
- Wiki Rotation (mathematics)
- Euler’s rotation theorem
- Maths - Rotation Matrices
- 繞任意軸旋轉
- Rotation About an Arbitrary Axis in 3 Dimensions
- Rotation about an Arbitrary Axis (Line)