by Alo?s Bissuel, Vincent Grosbois and Benjamin Heymann

Alo?sBissuel，Vincent Grosbois和Benjamin Heymann撰寫

The recent media debate on COVID-19 drugs is a unique occasion to discuss why decision making in an uncertain environment is a complicated but fundamental topic in our technology-based, data-fueled societies.

最近有關COVID-19藥物的媒體辯論是討論我們為何在以技術為基礎，以數據為動力的社會中為什么在不確定的環境中進行決策是一個復雜而基本的話題的難得的機會。

Aside from systematic biases — which are also an important topic —any scientific experiment is subject to a lot of unfathomable, noisy, or random phenomena.For example when one wants to know the effect of a drug on a group of patients, one may always wonder “If I were to take a similar group to renew the test, would I get the same result?” Such an experiment would at best end up with similar results. Hence the right question is probably something like “Would my conclusions still hold?” Several dangers await the uncautious decision-maker.

除了系統性偏見(這也是一個重要的話題)之外，任何科學實驗都受到許多難以理解，嘈雜或隨機現象的影響。例如，當一個人想知道某種藥物對一組患者的作用時，可能總是納悶：“如果我要參加一個類似的小組來延長考試時間，我會得到相同的結果嗎？” 這樣的實驗充其量只能得到相似的結果。 因此，正確的問題可能類似于“我的結論還成立嗎？” 謹慎的決策者有幾個危險等待著。

A first danger comes from the design and context of the experiment. Suppose you are given a billion dices, and that you roll each dice 10 times. If you get a dice that gave you ten times a 6, does it mean it is biased?This is possible, but on the other hand, the design of this experiment made it extremely likely to observe such an outlier, even if all dices are fair. In this case, the eleventh throw of this dice will likely not be a 6 again

第一個危險來自實驗的設計和環境 。 假設給您十億個骰子，并且將每個骰子擲10次。 如果您得到的骰子是6的10倍，是否表示它有偏見？這是可能的，但另一方面，本實驗的設計使其極有可能觀察到這樣的異常值，即使所有骰子都是公平。 在這種情況下，此骰子的第11次擲出可能不再是6

A second danger comes from human factors. In particular incentives and cognitive bias.Cognitive bias, because when someone is convinced of something, he is more inclined to listen to — and report — a positive rather than a negative signal.Incentives, because society — shall it be in the workplace, the media or scientific communities — is more inclined to praise statistically positive results than negative ones.For instance, suppose an R&D team is working on a module improvement by doing A/B tests. Suppose also that positive outcomes are very unlikely, and negative ones very likely, and that the result of experiments is noisy. An incautious decision-maker is likely to roll out more negative experiments than positive ones, hence the overall effort of the R&D team will end up deteriorating the module.

第二個危險來自人為因素 。 特別是動機和認知偏見 。 認知偏見 ，因為當某人確信某件事時，他更傾向于傾聽并報告正面的信號，而不是負面的信號。 激勵措施是因為社會(無論是在工作場所，媒體還是科學界)都應該贊揚統計學上的積極結果，而不是消極的結果。例如，假設一個研發團隊正在通過A / B測試來改進模塊。 還假設積極的結果是極不可能的，而消極的結果是極有可能的，并且實驗的結果是嘈雜的。 一個不謹慎的決策者可能會推出更多的負面實驗，而不是正面的實驗，因此研發團隊的整體努力最終會使模塊惡化。

At Criteo, we use A/B testing to make decision while coping with uncertainty. It is something we understand well because it is at the heart of our activities.Still, A/B testing raises many questions that are technically involved, and so require some math and statistical analysis. We propose to answer some of them in this blog post.

在Criteo，我們使用A / B測試來做出決策，同時應對不確定性。 我們很了解這是因為它是我們活動的核心。仍然，A / B測試提出了許多技術上涉及的問題，因此需要一些數學和統計分析。 我們建議在此博客文章中回答其中一些問題。

We will introduce several statistical tools to determine if an A/B-test is significant, depending on the type of metric we are looking at. We will focus first on additive metrics, where simple statistical tools give direct results, and then we will introduce the bootstrap method which can be used in more general settings.

我們將介紹幾種統計工具來確定A / B檢驗是否有效，具體取決于我們正在查看的指標類型。 我們將首先關注簡單的統計工具可直接得出結果的加性指標，然后我們將介紹可在更一般的設置中使用的引導方法。

如何總結A / B測試的重要性 (How to conclude on the significance of an A/B-test)

We will present good practices based on the support of the distribution (binary / non-binary) and on the type of metric (additive / non-additive).In the following sections, we will propose different techniques that allow us to assess if an A/B-test change is significant, or if we are not able to confidently conclude that the A/B-test had any effect.

我們將基于分布的支持(二進制/非二進制)和度量類型(加法/非加法)提出良好做法。在以下各節中，我們將提出不同的技術，使我們能夠評估A / B測試更改意義重大，或者如果我們無法自信地得出結論，A / B測試有效。

We measure the impact of the change done in the A/B-test by looking at metrics. In the case of Criteo, this metric could for instance be “the number of sales made by a user on a given period”.

我們通過查看指標來衡量在A / B測試中所做更改的影響。 在Criteo的情況下，該指標例如可以是“用戶在給定時期內的銷售數量”。

We measure the same metric on two populations: The reference and the test population. Each population has a different distribution, from which we gather data points (and eventually compute the metric). We also assume that the A/B-test has separated the population randomly and that the measures are independent with respect to each other.

我們在兩個總體上測量相同的指標：參考總體和測試總體。 每個總體都有不同的分布，從中我們可以收集數據點(并最終計算指標)。 我們還假設A / B檢驗已隨機分離了總體，并且這些度量相對于彼此是獨立的。

累加指標的一些特殊情況 (Some special cases for additive metrics)

Additive metrics can be computed at small granularity (for instance at the display or user level), and then summed up to form the final metric. Examples might include the total cost of an advertiser campaign (which is the sum of the cost of each display), or number of buyers for a specific partner.

可以以較小的粒度(例如在顯示級別或用戶級別)計算附加指標，然后將其加起來以形成最終指標。 例如，可能包括廣告客戶活動的總費用(即每次展示費用的總和)，或特定合作伙伴的購買者數量。

指標僅包含零或一 (The metric contains only zeros or ones)

At Criteo, we have quite a few binary metrics that we use for A/B-test decision making. For instance, we want to compare the number of users who clicked on an ad or better yet, the number of buyers in the two populations of the A/B-test. The base variable here is the binary variable X which represents if a user has clicked an ad or bought a product.

在Criteo，我們有很多二進制指標可用于A / B測試決策。 例如，我們要比較點擊廣告的用戶數量或更好的用戶，即A / B測試兩個人群中的購買者數量。 這里的基本變量是二進制變量X，它表示用戶是否單擊了廣告或購買了產品。

For this type of variable, the test to use is a chi-squared Pearson test.

對于此類變量，要使用的檢驗是卡方皮爾遜檢驗。

Let us say we want to compare the number of buyers between the reference population and the test population. Our null statistical hypothesis H0 is that the two populations have the same buying rate. The alternative hypothesis H1 is that the two populations do not have the same buying rate. We will fix the p-value to 0.05 for instance (meaning that we will accept a deviation of the test statistic to its 5% extremes under the null hypothesis before we reject it).

假設我們要比較參考人口和測試人口之間的購買者數量。 我們的無效統計假設H0是兩個總體具有相同的購買率。 備選假設H1是兩個總體的購買率不同。 例如，我們會將p值固定為0.05(這意味著在我們接受無效假設之前，我們將接受檢驗統計量與其5％極值之間的偏差)。

We have gathered the following data:

我們收集了以下數據：

Under the null hypothesis, population A and B are sampled from the same distribution, so that the empirical distribution of the sum of the two populations can be taken as the generative reference distribution. Here we get a conversion rate close to 1%.

在零假設下，從相同的分布中采樣總體A和B，因此可以將兩個總體之和的經驗分布作為生成參考分布。 在這里，我們獲得了接近1％的轉化率。

Using this conversion rate for both populations, as the null hypothesis states, we can compute the expected distribution of buyers for populations A and B.

如原假設所述，使用兩個人口的轉換率，我們可以計算人口A和人口B的購買者的預期分布。

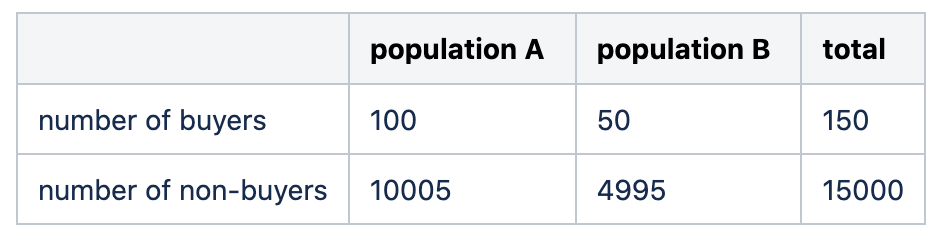
The chi-2 statistics is the sum, for all cells, of the square of the difference between the expected value and the real value, divided by the expected value. Here we get x2 = 0.743. We have chosen a p-value of 0.05, and thus for this two degree of freedom chi-2 distribution, the statistic needs to be inferior to 3.8. We accept the H0 hypothesis so that we deem this A/B-test as neutral.

chi-2統計量是所有單元格的期望值和實際值之差的平方的總和除以期望值。 在這里我們得到x2 = 0.743。 我們選擇的p值為0.05，因此對于這兩個自由度chi-2分布，統計量應低于3.8。 我們接受H0假設，因此我們認為此A / B檢驗為中性。

Note that this test naturally accommodates unbalanced populations (as here the population B is half the size of the population A).

請注意，此測試自然可以容納不平衡的總體(因為此處的總體B是總體A的一半)。

加性指標的一般情況 (General case for an additive metric)

When the additive metric is not composed of only zeros and ones, the central limit theorem can be used to derive instantly the confidence interval of the metric. The central limit theorem tells us that the distribution of the mean of i.i.d. variables follows a normal distribution of known parameters. By multiplying by the total number of summed elements, this gives us the confidence bound for the sum.

當加性度量不僅由零和一組成時，可以使用中心極限定理立即導出度量的置信區間。 中心極限定理告訴我們， iid變量的均值分布遵循已知參數的正態分布。 通過將求和元素的總數乘以，便得出了求和結果的置信區間。

In the case of an A/B-test, things are a little bit more complicated as we need to compare two sums. Here, the test to use is a variant of the Student t-test. As the variance of the two samples are not expected to be the same, we have to use the specific version of the test which is adapted to this situation. It is called the Welch’s t-test. As for any statistical test, one needs to compute the statistic of the test, and compare it to the decision value given by the p-value chosen beforehand.

在A / B測試的情況下，由于我們需要比較兩個總和，所以事情要復雜一些。 在這里，要使用的測試是Student t-test的變體。 由于兩個樣本的方差預計不會相同，因此我們必須使用適合這種情況的特定版本的測試。 這稱為韋爾奇t檢驗 。 對于任何統計檢驗，都需要計算檢驗的統計量，并將其與預先選擇的p值給出的決策值進行比較。

This method has a solid statistical basis and is computationally very efficient, as it only needs the mean and the variance of the statistic over the two populations.

該方法具有扎實的統計基礎，并且計算效率很高，因為它只需要兩個總體的統計量的均值和方差即可。

指標沒有特殊屬性 (The metric has no special property)

The bootstrap method enables to conclude in this general case. We will present two versions of it. First, we introduce the exact one, which happens to be non-distributed. To accommodate larger data sets, a distributed version will be presented afterwards.

引導程序方法可以在這種一般情況下得出結論。 我們將介紹它的兩個版本。 首先，我們介紹確切的一個，它恰好是非分布式的。 為了容納更大的數據集，之后將提供分布式版本。

引導程序方法(非分布式) (Bootstrap method (non-distributed))

Bootstrapping is a statistical method used for estimating the distribution of a statistic. It was pioneered by Efron in 1979. Its main strength is its ease of application on every metric, from the most simple to the most complicated. There are some metrics where you cannot apply the Central Limit Theorem, as for instance the median (or any quantile), or for a more business-related one, the cost per sale (it is a ratio of two sums of random variables). Its other strength lies in the minimal amount of assumptions needed to use it, which makes it a method of choice in most situations.

自舉是一種統計方法，用于估計統計信息的分布。 它是埃夫隆(Efron)于1979年率先提出的。它的主要優點是易于在每個度量標準中使用，從最簡單到最復雜。 在某些度量標準中，您無法應用中央極限定理，例如中位數(或任何分位數)，或者與業務相關的度量標準，即每次銷售成本(它是兩個隨機變量之和的比率)。 它的其他優勢在于使用它所需的最少假設量，這使其成為大多數情況下的一種選擇方法。

The exact distribution of the metric can never be fully known. One good way to get it would be to reproduce the experiment which led to the creation of the data set many times and compute the metric each time. This would be of course extremely costly, not to mention largely impractical when an experiment cannot be run exactly the same twice (such as when some sort of feedback exists between the model being tested in the experiment and the results).

指標的確切分布永遠無法完全了解。 獲得它的一種好方法是重現導致多次創建數據集的實驗，并每次計算度量。 當然這將是極其昂貴的，更不用說當實驗不能完全相同地運行兩次時(例如，當實驗中的模型與結果之間存在某種反饋時)，這在很大程度上是不切實際的。

Instead, the bootstrap method starts from data set as an empirical distribution and replays “new” experiments by drawing samples (with replacement) from this data set. This is infinitely more practical than redoing the experiment many times. It has, of course, a computational cost of recreating (see below for a discussion of how many) an entire data set by sampling with replacement. The sampling is done using a binomial law of parameters (n, 1/n).

相反，bootstrap方法從數據集開始作為經驗分布，并通過從該數據集中抽取樣本(替換)來重放“新”實驗。 這比多次重做實驗更加實用。 當然，通過替換采樣來重新創建整個數據集會產生一定的計算成本(請參閱下文中的討論)。 使用參數(n，1 / n)的二項式定律進行采樣。

引導方法：實用的演練 (Bootstrap method: A practical walk-through)

1. First, decide on the number k of bootstraps you want to use. A reasonable number should be at least a hundred, depending on the final use of the bootstraps.

   首先，確定您要使用的引導程序的數量k 。 合理的數量應至少為一百，這取決于引導程序的最終用途。

2. For every bootstrap to be computed, recreate a data set from the initial one with random sampling with replacement, this new data set having the same number of examples than the reference data set.
   對于要計算的每個引導程序，請從初始樣本集重新創建一個數據集，并通過隨機抽樣進行替換，該新數據集的示例數與參考數據集相同。
3. Compute the metric of interest on this new data set.
   計算此新數據集上的關注指標。

4. Use the k values of the metric either to conclude on the statistical significance of the test.

   使用度量的k值可以得出測試的統計顯著性。

在A / B測試的情況下如何使用引導程序 (How to use bootstraps in the case of an A/B-test)

When analyzing an A/B-test, there is not only one but two bootstraps to be made. The metric has to be bootstrapped on both populations. The bootstrapped difference of the metric between the two populations can be simply computed by subtracting the unsorted bootstraps of the metric of one population with the other. For additive metrics, this is equivalent to computing on the whole population a new metric which the same on one population and minus the previous one on the other population.

分析A / B測試時，不僅要進行一次引導，而且要進行兩次引導。 該指標必須在兩個人群中都具有優勢。 可以通過將一個總體的指標的未排序引導程序與另一個總體相減來簡單計算兩個指標之間的自舉差異。 對于加性指標，這等效于在整個總體上計算一個新指標，該新指標在一個總體上相同，而在另一個總體上減去前一個指標。

The bootstrapping has to be done in a fashion compatible with the split used for the A/B-test. Let us illustrate this by an example. At Criteo, we do nearly all our A/B-tests on users. We also think that most of the variability we see in our metrics comes from the users, so we bootstrap our metrics on users.

自舉必須以與用于A / B測試的拆分兼容的方式進行。 讓我們通過一個例子來說明這一點。 在Criteo，我們幾乎對用戶進行所有A / B測試。 我們還認為，我們在指標中看到的大多數可變性都來自用戶，因此我們將指標引導到用戶身上。

Finally, if the populations have different sizes, additive metrics need to be normalized so that the smaller population is comparable to the larger. This is not neccessary for intensive metrics (such as conversion rate or averages). For instance, to compare the effect of lighting conditions on the number of eggs laid in two different chicken coops, one larger than the other, the number of eggs has to be resized so that the two chicken coops are made of the same arbitrary size (note that here, we do not resize the number of chicken, as there might be no fixed relation between the size of the coop and the number of chicken). But studying the average number of eggs laid by every hen, no such resizing is needed (as it is already done by the averaging).

最后，如果總體大小不同，則需要對附加指標進行標準化，以便較小的總體與較大的總體具有可比性。 對于密集指標(例如轉化率或平均值)，這不是必需的。 例如，為了比較光照條件對兩個不同雞舍產下的雞蛋數量(一個大于另一個)的影響，必須調整雞蛋的大小，以使兩個雞舍都具有相同的任意大小(請注意，在這里，我們沒有調整雞的數量，因為雞舍的大小和雞的數量之間可能沒有固定的關系。 但是，通過研究每只母雞產下的雞蛋的平均數量，就不需要進行這種大小調整(因為平均已經完成了)。

如何得出A / B檢驗的重要性的結論？ (How to conclude on the significance of the A/B-test?)

The bootstrap method gives an approximation of the distribution of the metric. This can be used directly in a statistical test, either non-parametric or parametric. For instance, given the distribution of the difference of some metric between the two populations, a non-parametric test would be, given H0 “the two population are the same, ie the difference of the metric should be zero” and a p-value of 0.05, to compute the quantiles [ 2.5%, 97.5%] by ordering the bootstrapped metric, and conclude that H0 is true if 0 is inside this confidence interval. Other methods exist for computing a confidence interval from a bootstrapped distribution. A parametric test would for example interpolate the distribution of the metric by a normal one (using the mean and the variance computed from the bootstraps) and conclude that H0 is true if 0 is less than (approximately) two standard deviations away from the mean. This is true only for metrics whose distribution is approximately normal (for instance a mean value, where the central limit theorem will apply).

引導程序方法給出了度量分布的近似值。 這可以直接用于非參數或參數的統計測試中。 例如，給定兩個總體之間某個度量標準差的分布，則給定H0，“兩個總體相同，即度量標準差應為零”，并給出p值，這將是一個非參數檢驗。取0.05，以通過對自舉度量進行排序來計算分位數[2.5％，97.5％]，并得出結論，如果0在此置信區間內，則H0為真。 存在用于根據自舉分布計算置信區間的其他方法 。 例如，參數測試將通過一個正態插值來度量的分布(使用均值和自舉計算得出的方差)，并得出結論：如果0小于(近似)遠離均值的兩個標準差，則H0為真。 這僅適用于分布近似正態的度量(例如，平均值，將應用中心極限定理)。

圖解的例子 (An illustrated example)

To explain how to use the bootstrap method for A/B-testing, let us go through a very easy example. Two populations A and B have both one million users each, and we are looking at the number of people who bought a product. For our synthetic example, population A has a conversion rate of exactly one percent, whereas population B has a conversion rate of 1.03%. We simulate the two datasets using Bernouilli trials, and end up with 10109 buyers in population A, and 10318 buyers in population B. Note that the empirical conversion rate of population A deviates far more from the true rate than for population B. The question asked is “Is the difference of the number of buyers significant?”. The null hypothesis is that the two populations are generated from the same distribution. We will take a confidence interval of [2.5%; 97.5%] to conclude.

為了說明如何使用引導方法進行A / B測試，我們來看一個簡單的示例。 A和B這兩個人群分別擁有100萬用戶，我們正在研究購買產品的人數。 對于我們的綜合示例，群體A的轉化率恰好為1％，而群體B的轉化率為1.03％。 我們使用Bernouilli試驗模擬這兩個數據集，最終得到人口A的10109個購買者和人口B的10318個購買者。請注意，人口A的經驗轉化率與真實比率的偏離遠大于人口B的真實轉化率。是“購買者數量差異顯著嗎？”。 零假設是兩個總體由相同的分布生成。 我們將置信區間為[2.5％； 97.5％]得出結論。

We use a thousand bootstraps to see the empirical distribution of the number of buyers in both populations. Here is a plot below of the histogram of the bootstraps:

我們使用一千個引導程序來查看兩個人群中購買者數量的經驗分布。 這是引導程序直方圖的下方圖：

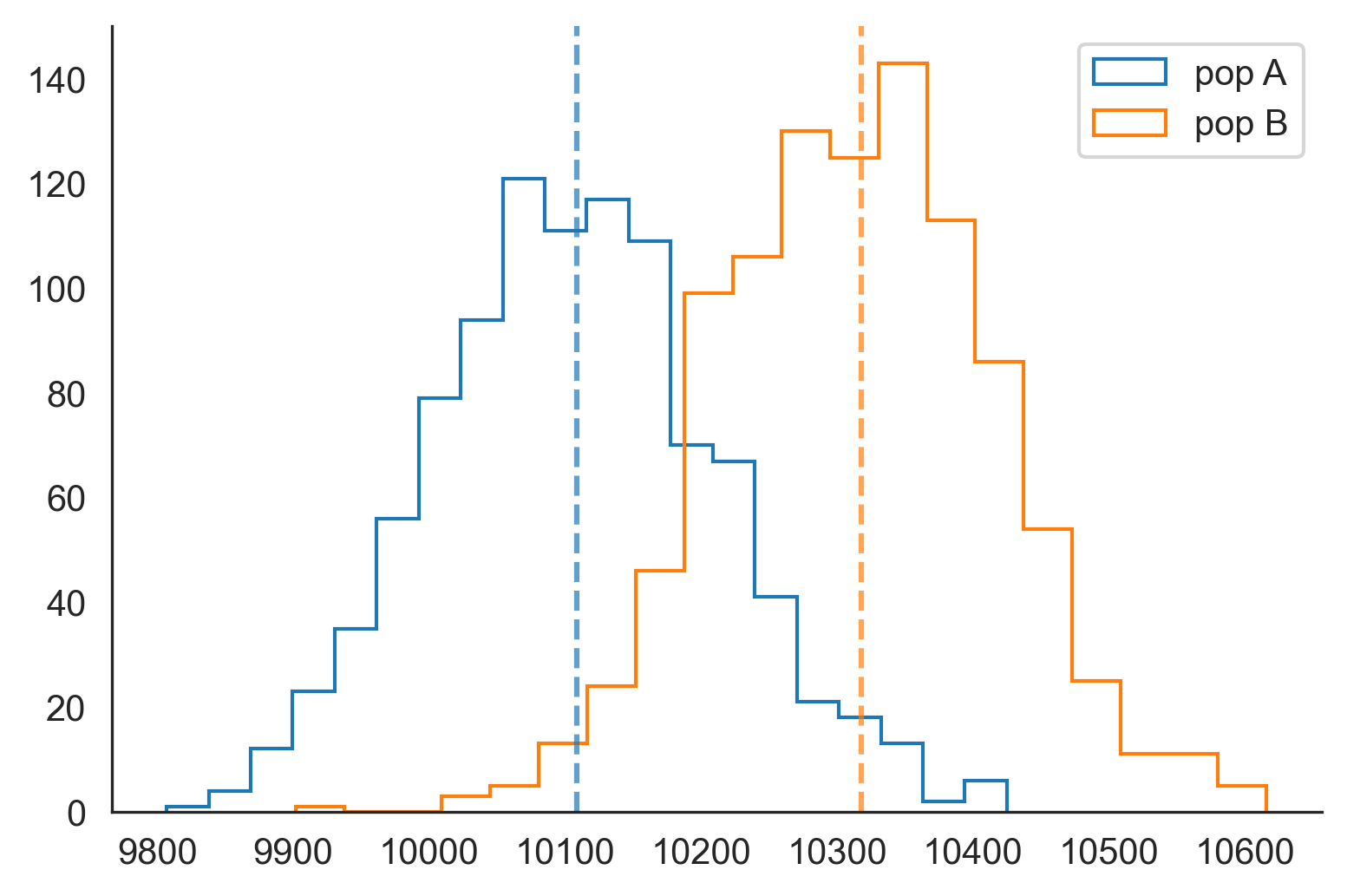
As predicted by the central limit theorem, the distributions are roughly normal and centered around the empirical number of buyers (dashed vertical lines). The two distributions overlap.

正如中心極限定理所預測的那樣，分布大致呈正態分布，并以購買者的經驗數量為中心(垂直虛線)。 這兩個分布重疊。

To find the distribution of the difference of the number of buyers, the bootstraps of both populations are randomly shuffled and subtracted one by one. Another way to look at it is to concatenate the two data sets together and create a metric with a +1 for a buyer in A and -1 for a buyer in B. The sum of this metric gives the difference of number of buyers in the two populations. If the random sampling is compatible with the population split, this gives exactly the same result. Below is the result of this operation. As expected by the central limit theorem, this is a normal distribution. The color indicates if a bootstrap is positive or negative.

為了找到購買者數量差異的分布，隨機調整兩個種群的引導程序，并一一減去。 另一種看待它的方法是將兩個數據集連接在一起，并創建一個度量標準，其中A中的買方為+ 1，B中的買方為-1。該度量的總和給出了A中買方的數量差異。兩個人口。 如果隨機抽樣與總體劃分兼容，則得出的結果完全相同。 以下是此操作的結果。 正如中心極限定理所期望的，這是一個正態分布。 顏色指示引導程序是正還是負。

In this case, the number of positive bootstraps is 74 out of 1000. This means that only 7.4% of bootstraps show a positive difference inside the confidence interval of [2.5%; 97.5%] which we decided earlier on. Subsequently, we cannot reject the null hypothesis. We can only say that the A/B-test is inconclusive.

在這種情況下，正引導程序的數量為1000的74。這意味著，只有7.4％的引導程序在置信區間[2.5％; 97.5％]。 隨后，我們不能拒絕原假設。 我們只能說A / B測試沒有定論。

Bootstrap方法(分布式) (Bootstrap method (distributed))

When working with large-scale data, several things can happen to the data set:

當使用大規模數據時，數據集可能會發生幾件事情：

• The data set is distributed across machines and too big to fit into a single’s machine memory
  數據集分布在計算機之間，并且太大而無法容納一個人的計算機內存
• The data set is distributed across machines and even though it could fit into a single machine, it is costly and impractical to collect everything on a single machine
  數據集分布在多臺計算機上，即使它可以放入一臺計算機中，也要在一臺計算機上收集所有數據，這既昂貴又不切實際

• The data set is distributed across machines and even the values of an observation are distributed across machines. For instance, it happens if the observation we are interested in is “how much did the user spend for all his purchases in the last 7 days” and if our data set contains data at purchase-level. To apply the previous methods, we would first need to regroup our purchase-level data set into a user-level data set, which can be costly.

  該數據集跨機器分布和觀察甚至值被跨越機器分布。 例如，如果我們感興趣的觀察結果是“用戶在過去7天內花了多少錢購買所有商品”并且我們的數據集包含購買級別的數據，就會發生這種情況。 要應用先前的方法，我們首先需要將購買級別的數據集重新分組為用戶級別的數據集，這可能會花費很大。

In this section, we describe a bootstrap algorithm that can work in this distributed setting. As it is also able to work on any distribution type, it is thus the most general algorithm to get confidence intervals.Let us first define k, the number of resamplings that we will do over the distribution of X (usually, at least 100). To get S1, the sum of the first resampled draw, we would normally draw with replacement n elements from the series of X_i, and then sum them.

在本節中，我們描述了可以在此分布式設置中工作的引導程序算法。 由于它也可以處理任何分布類型，因此它是獲取置信區間的最通用算法。讓我們首先定義k，即在X的分布上(通常至少100)進行重采樣的次數。 。 為了得到S1，即第一次重采樣的和，我們通常用X_i系列中的替換n個元素進行繪畫，然后將它們求和。

However, in a distributed setting, it might be impossible or too costly to do a draw with replacement of the distributed series X_i. We instead use an approximation: Sum each element of the data set, weighted with a weight drawn from a Poisson(1) distribution. This weight is also “seeded” by both; the bootstrap population id (so from 1 to k) and also an identifier that represents the aggregation level our data should be grouped by. Doing this ensures that, if we go by the previous example, purchases made by the same user get the same weight for a given bootstrap resampling: We get the same end result as if we had already grouped the data set by user in the first place.

但是，在分布式環境中，用替換分布式系列X_i進行抽獎可能是不可能的，或者成本太高。 相反，我們使用一個近似值：對數據集的每個元素求和，并使用從Poisson(1)分布中得出的權重進行加權。 雙方也都“擔負”了這一責任； 引導程序人口ID(從1到k)，以及代表我們的數據應歸類的聚合級別的標識符。 這樣做可以確保，如果我們按照前面的示例進行操作，則在給定的引導程序重采樣下，同一用戶購買的商品將獲得相同的權重：我們得到的最終結果與首先將用戶對數據集進行分組的結果相同。

We thus obtain S1, an approximate version of the sum from resampled data. Once we obtain the S1… S_k series, we use this as a proxy for the real distribution of S and can then take the quantiles from this series. Note that this raises 2 issues:

因此，我們從重新采樣的數據中獲得S1，即總和的近似版本。 一旦獲得S1…S_k系列，就可以將其用作S實際分布的代理，然后可以從該系列中獲取分位數。 請注意，這引起了兩個問題：

• An approximation error is made due to the fact that the number of bootstraps is finite (the bootstrap method converges for an infinite number of resampling)
  由于引導程序的數量是有限的，所以會產生近似誤差(引導程序方法收斂于無限數量的重采樣)

• An approximation error that induces a bias in the measure of quantiles is made due to the fact that the resampling is done approximately. This comes from the fact that for a given resampling, the sum of the weights is not exactly equal to n (this is only true on average). For further reading, check out this great blog post and the associated scientific paper.

  由于重采樣是近似完成的，所以會產生一個近似誤差，該誤差會導致分位數的度量產生偏差。 這源于以下事實：對于給定的重采樣，權重的總和不完全等于n(這僅在平均值上正確)。 如需進一步閱讀，請查看這篇出色的博客文章和相關的科學論文 。

摘要 (Summary)

比較利弊 (Comparative pro/cons)

Here is a short table highlighting the pros and cons of each method.

這是一張簡短的表格，突出了每種方法的優缺點。

結論 (Conclusion)

In this article, we have detailed how to analyze A/B-tests using various methods, depending on the type of metric which is analyzed and the amount of data. While all methods have their advantages and their drawbacks, we tend to use bootstraps most of the time at Criteo, because it is usable in most cases and lends itself well to distributed computing. As our data sets tend to be very large, we always use the distributed bootstraps method. We would not be able to afford the numerical complexity of the exact bootstrap method.

在本文中，我們詳細介紹了如何根據所分析的指標類型和數據量，使用各種方法來分析A / B測試。 盡管所有方法都有其優點和缺點，但我們大多數時候傾向于在Criteo中使用引導程序，因為它在大多數情況下都可用并且非常適合于分布式計算。 由于我們的數據集往往非常大，因此我們始終使用分布式引導程序方法。 我們將無法負擔精確自舉方法的數值復雜性。

We also think that using the Chi-2 and T-test methods from time to time is useful. Using these methods forces you to follow the strict statistical hypothesis testing framework, and ask yourself the right questions. As you may find yourself using the bootstrap method a lot, it allows to keep a critical eye on it, and not take blindly its figures for granted!

我們還認為，不時使用Chi-2和T檢驗方法是有用的。 使用這些方法會迫使您遵循嚴格的統計假設檢驗框架，并向自己提出正確的問題。 您可能會發現自己經常使用bootstrap方法，因此它可以使您始終保持批判的眼光，而不會盲目地將其數字視為理所當然！

關于作者 (About the authors)

Alo?s Bissuel, Vincent Grosbois and Benjamin Heymann work in the same team at Criteo, working on measuring all sorts of things.

Alo?sBissuel，Vincent Grosbois和Benjamin Heymann在Criteo的同一團隊中工作，致力于測量各種事物。

Benjamin Heymann is a senior researcher, while Alo?s Bissuel and Vincent Grosbois are both senior machine learning engineers.

Benjamin Heymann是高級研究員，而Alo?sBissuel和Vincent Grosbois都是高級機器學習工程師。

Like what you are reading? Check out our latest articles on Medium.

喜歡您正在閱讀的內容嗎？ 查看我們有關Medium的最新文章。

Interested in joining Criteo and help continue this article? Check out our current openings!

有興趣加入Criteo并幫助繼續本文嗎？ 查看我們當前的空缺！