因為這章內容比較多，分開來敘述，前面先講理論后面是講代碼。最重要的是代碼部分，結合代碼去理解思想。

SGD優化器

思想：

根據梯度，控制調整權重的幅度

公式：

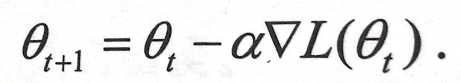
權重(新) = 權重(舊) - 學習率 × 梯度

Adam優化器

思想：

在我看來，Adam優化器重點是能動態調整學習率，防止學習率較大時反復震蕩，比如說當梯度一直為正的時候，權重一直減小，這時直到梯度為負的時候，權重不應該一下子增長太多，而是應該緩慢增長。

這個公式可以在Diy框架代碼中找到對應的代碼并進行了解釋。

優勢：

1. 實現簡單，計算高效，對內存需求少
2. 超參數具有很好的解釋性，且通常無需調整或僅需很少的微調
3. 更新的步長能夠被限制在大致的范圍內（初始學習率）
4. 能夠表現出自動調整學習率
5. 很適合應用于大規模的數據及參數的場景
6. 適用于不穩定目標函數
7. 適用于梯度稀疏或梯度存在很大噪聲的問題

BP反向傳播

傳播過程：

1.根據輸入x和模型當前權重，計算預測值y’

2.根據y’和y使用loss函數計算loss

3.根據loss計算模型權重的梯度

4.使用梯度和學習率，根據優化器調整模型權重

Pytorch框架下實現代碼：

import torch
import torch.nn as nn
import numpy as np
import copy"""
基于pytorch的網絡編寫
實現梯度計算和反向傳播
加入激活函數
"""class TorchModel(nn.Module):def __init__(self, hidden_size):super(TorchModel, self).__init__()self.layer = nn.Linear(hidden_size, hidden_size, bias=False)    #線性層,輸入輸出維度都是hidden_sizeself.activation = torch.sigmoid     #套一個激活函數（不套也可以）self.loss = nn.functional.mse_loss  #loss采用均方差損失#當輸入真實標簽，返回loss值；無真實標簽，返回預測值def forward(self, x, y=None):y_pred = self.layer(x)          #將輸入放入線性層中，獲得預測值y_pred = self.activation(y_pred)    #將預測值激活if y is not None:return self.loss(y_pred, y)else:return y_predx = np.array([1, 2, 3, 4])  #輸入
y = np.array([3, 2, 4, 5])  #預期輸出#torch實驗
torch_model = TorchModel(len(x))    #給torchmodel函數傳入x的維度作為hidden_size
torch_model_w = torch_model.state_dict()["layer.weight"]
print(torch_model_w, "初始化權重")
numpy_model_w = copy.deepcopy(torch_model_w.numpy())    #拷貝一下，用于diy中對初始權重計算torch_x = torch.FloatTensor([x])
torch_y = torch.FloatTensor([y])#torch的前向計算過程，得到loss
torch_loss = torch_model.forward(torch_x, torch_y)
print("torch模型計算loss：", torch_loss)#設定優化器
learning_rate = 0.1
optimizer = torch.optim.SGD(torch_model.parameters(), lr=learning_rate)     #SGD優化器
#torch_model.parameters傳遞模型中所有的參數，也可以只有選擇想傳遞的參數
# optimizer = torch.optim.Adam(torch_model.parameters())		#Adam優化器
optimizer.zero_grad()   #先把優化器歸零#pytorch的反向傳播操作
torch_loss.backward()       #完成梯度計算
print(torch_model.layer.weight.grad, "torch 計算梯度")  #查看某層權重的梯度#torch梯度更新
optimizer.step()#查看更新后權重
update_torch_model_w = torch_model.state_dict()["layer.weight"]
print(update_torch_model_w, "torch更新后權重")

接下來是DIY手動框架實現

"""
手動實現梯度計算和反向傳播
加入激活函數
"""
#自定義模型，接受一個參數矩陣作為入參
class DiyModel:def __init__(self, weight):self.weight = weightdef forward(self, x, y=None):y_pred = np.dot(self.weight, x)y_pred = self.diy_sigmoid(y_pred)if y is not None:return self.diy_mse_loss(y_pred, y)else:return y_pred#sigmoiddef diy_sigmoid(self, x):return 1 / (1 + np.exp(-x))#手動實現mse，均方差lossdef diy_mse_loss(self, y_pred, y_true):return np.sum(np.square(y_pred - y_true)) / len(y_pred)#手動實現梯度計算def calculate_grad(self, y_pred, y_true, x):#前向過程與反向過程對比看# wx = np.dot(self.weight, x)# sigmoid_wx = self.diy_sigmoid(wx)# loss = self.diy_mse_loss(sigmoid_wx, y_true)#反向過程（通過前向的loss來獲得對權重w的導數）# 均方差函數 (y_pred - y_true) ^ 2 / n 的導數 = 2 * (y_pred - y_true) / ngrad_loss_sigmoid_wx = 2/len(x) * (y_pred - y_true)# sigmoid函數 y = 1/(1+e^(-x)) 的導數 = y * (1 - y)grad_sigmoid_wx_wx = y_pred * (1 - y_pred)# wx對w求導 = xgrad_wx_w = x#導數鏈式相乘grad = grad_loss_sigmoid_wx * grad_sigmoid_wx_wxgrad = np.dot(grad.reshape(len(x),1), grad_wx_w.reshape(1,len(x)))  #轉化為矩陣形式相乘return grad#sgd梯度更新
def diy_sgd(grad, weight, learning_rate):return weight - grad * learning_rate#adam梯度更新
def diy_adam(grad, weight):#參數應當放在外面，此處為保持后方代碼整潔簡單實現一步alpha = 1e-3  #學習率beta1 = 0.9   #超參數（推薦）beta2 = 0.999 #超參數（推薦）eps = 1e-8    #超參數t = 0         #初始化mt = 0        #初始化vt = 0        #初始化#開始計算t = t + 1gt = gradmt = beta1 * mt + (1 - beta1) * gt      #前面的mt累積在后面的mt中，使前面的梯度占高比例，本輪的占低比例vt = beta2 * vt + (1 - beta2) * gt ** 2mth = mt / (1 - beta1 ** t)     #分母不斷增大，mth不斷減小vth = vt / (1 - beta2 ** t)weight = weight - alpha * mth / (np.sqrt(vth) + eps)    #alpha學習率動態調整return weight#手動實現loss計算
diy_model = DiyModel(numpy_model_w)
diy_loss = diy_model.forward(x, y)
print("diy模型計算loss：", diy_loss)#手動實現反向傳播
grad = diy_model.calculate_grad(diy_model.forward(x), y, x)
print(grad, "diy 計算梯度")     #梯度的維度應與矩陣維度一致#手動梯度更新
diy_update_w = diy_sgd(grad, numpy_model_w, learning_rate)	#grad優化器
# diy_update_w = diy_adam(grad, numpy_model_w)		#adam優化器
print(diy_update_w, "diy更新權重")

運行結果：

SGD優化器情況下：

Adam優化器的情況下：