In a previous article, I outlined the limitations of conventional time series models such as ARIMA when it comes to forecasting extreme temperature values, which in and of themselves are outliers in the time series.

在上一篇文章中 ，我概述了常規時間序列模型(如ARIMA)在預測極端溫度值時的局限性，而極端溫度值本身就是時間序列中的異常值。

When dealing with extreme values, a Monte Carlo simulation can be a better solution in terms of quantifying the probability of an extreme event occurring.

在處理極端值時，就量化極端事件發生的可能性而言，蒙特卡洛模擬可能是更好的解決方案。

背景 (Background)

In the last example, the mean minimum monthly temperature values for Braemar, Scotland were used in training and validating an ARIMA model forecast. This was done using monthly Met Office data from January 1959 — July 2020 (contains public sector information licensed under the Open Government Licence v1.0).

在最后一個示例中，蘇格蘭Braemar的平均最低最低氣溫值用于訓練和驗證ARIMA模型預測。 這是使用1959年1月至2020年7月的大都會辦公室每月數據 (包含根據《公開政府許可證v1.0》 許可的公共部門信息)完成的。

In this instance, a Monte Carlo simulation is built on the same data in an attempt to generate a scenario analysis of a range of temperature values.

在這種情況下，基于相同的數據進行蒙特卡洛模擬，以嘗試生成一系列溫度值的方案分析。

Firstly, let’s take a closer look at the data itself.

首先，讓我們仔細看看數據本身。

This is the mean monthly minimum temperature for Braemar:

這是Braemar的平均每月最低溫度：

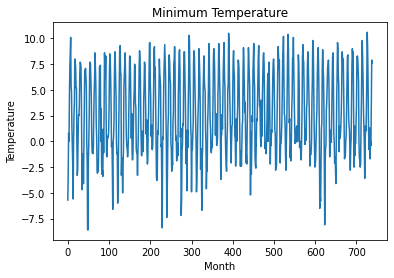
Let’s analyse the time series in more detail. Firstly, let’s plot a histogram of the distribution:

讓我們更詳細地分析時間序列。 首先，讓我們繪制分布的直方圖：

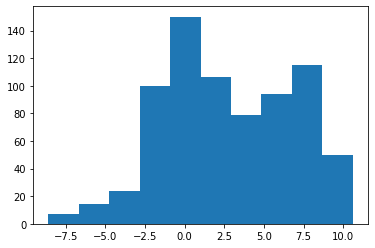
From looking at the histogram, we can see that the distribution shows negative skew. Let’s calculate this to confirm.

通過查看直方圖，我們可以看到分布顯示為負偏斜。 讓我們計算一下以確認。

>>> series = value;
>>> skewness = series.skew();
>>> print("Skewness:");
>>> print(round(skewness,2));Skewness:
-0.05

From this analysis, we observe that the distribution is negatively skewed, and therefore doesn’t necessarily follow a normal distribution (at least not fully).

通過此分析，我們觀察到分布呈負偏斜，因此不一定遵循正態分布(至少不完全呈正態分布)。

Here is a QQ plot of the residuals:

這是殘差的QQ圖：

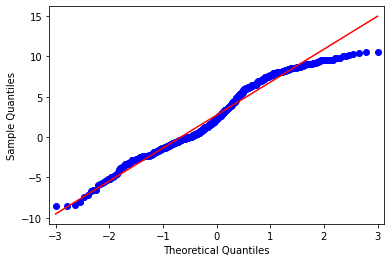
In particular, we can see that values in the upper quantiles deviate from the normal distribution line. With a median temperature of 2.2°C and a mean temperature of 2.72°C (Braemar is one of the coldest areas of the United Kingdom), values significantly above this lie outside the bounds of a normal distribution — we would expect that with lower temperatures recorded in the upper quantiles — the distribution would assume a more normally-shaped pattern.

特別是，我們可以看到較高分位數中的值偏離了正態分布線。 平均溫度為2.2°C，平均溫度為2.72°C(寶馬山是英國最冷的地區之一)，高于此值的值不在正態分布范圍內-我們希望溫度較低時記錄在較高的分位數中-分布將呈現更正常的形狀。

Additionally, modelling weather patterns can be quite tricky as the distribution will vary based on geography. For instance, temperature distribution at the equator will be quite different to that of the poles. In this regard, understanding the distribution of the time series in question is necessary in order to model weather simulations accurately.

此外，對天氣模式進行建模可能會非常棘手，因為分布會根據地理位置而變化。 例如，赤道的溫度分布將與兩極的溫度分布完全不同。 在這方面，有必要了解有關時間序列的分布，以便準確地模擬天氣模擬。

蒙特卡羅模擬 (Monte Carlo Simulation)

For this simulation, 1000 random values are generated. Since the distribution has been identified as negatively skewed, this means that the generated random values must also follow a similar negatively skewed distribution.

對于此仿真，將生成1000個隨機值。 由于已將分布標識為負偏斜，因此這意味著生成的隨機值也必須遵循類似的負偏斜分布。

預測每月最低溫度 (Forecasting Monthly Temperature Minimums)

To do this, skewnorm from the scipy library can be used. As was previously indicated, a (or the skew parameter) is set to -0.05.

為此， skewnorm 可以從scipy庫中使用。 如前所述，a(或偏斜參數)設置為-0.05 。

from scipy.stats import skewnorm
a=-0.05
distribution = skewnorm.rvs(a, size=1000)

Here is a sample of the generated array:

這是生成的數組的示例：

array([ 1.10993586e-01,  1.92293755e+00, -1.29797928e+00, -1.36817895e+00,
       -4.08836917e-01, -2.20566871e-01, -1.80936352e+00,
...
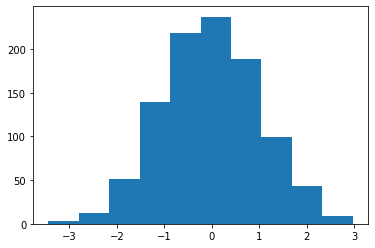
-1.59656083e-01,  2.10239315e+00,  1.98068918e-01, -2.23784665e-01])

Here is a plot of the generated data, which shows a very slight negative skew:

這是生成的數據圖，顯示了非常輕微的負偏斜：

The mean and standard deviation for the original series is calculated:

計算原始序列的均值和標準差：

>>> mu=np.mean(value)
>>> mu
2.7231393775372124>>> sigma=np.std(value)
>>> sigma
4.082818933287181

Now, the generated random numbers that form the assumed distribution are multiplied by sigma (standard deviation), with the product then added to mu (the mean).

現在，將形成假定分布的生成的隨機數乘以sigma(標準差)，然后將乘積加到mu(平均值)上。

y = mu + sigma*distribution
num_bins = 50

Here is another example of this procedure (with a normal distribution being assumed). Let’s generate a histogram of the temperature simulations:

這是此過程的另一個示例 (假設正態分布)。 讓我們生成溫度模擬的直方圖：

# Histogram
plt.hist(y, num_bins, facecolor='green', alpha=0.5)
plt.xlabel('Values')
plt.ylabel('Frequency')
plt.title(r'Histogram of Temperature Simulations')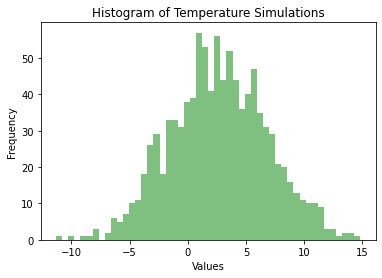

You will notice that the lowest simulated temperature of -11.32°C lies just below the lowest mean monthly temperature value of -8.6°C as recorded in the original data. From that standpoint, the model did reasonably well in estimating the extreme minimum values that could be expected on a monthly basis.

您會注意到，最低模擬溫度-11.32°C恰好低于原始數據中記錄的最低平均每月溫度值-8.6°C。 從這個角度來看，該模型在估計每月可能期望的極小最小值方面表現相當不錯。

預測每日最低溫度 (Forecasting Daily Temperature Minimums)

That said, a limitation in this example is that we are working with monthly data — not daily.

就是說，此示例中的局限性在于我們正在使用每月數據，而不是每天。

Suppose we wished to predict the lowest daily minimum temperature instead. Would this model be of use in this scenario?

假設我們希望預測最低的每日最低溫度。 此模型在這種情況下會有用嗎？

In fact, the lowest recorded daily minimum temperature for Braemar came in at -27.2°C on 10 January 1982, which greatly exceeds the lowest simulated temperature of -11.32°C by the Monte Carlo model.

實際上，1982年1月10日， 寶馬汽車的最低記錄每日最低溫度為-27.2°C，大大超過了蒙特卡洛模型的最低模擬溫度-11.32°C。

This indicates that the distribution may be more negatively skewed than the monthly data suggests. Use of daily data might show greater negative skew, and may be more informative for the Monte Carlo simulation.

這表明該分布可能比月度數據顯示的負偏斜更大。 每日數據的使用可能顯示更大的負偏斜，并且對于蒙特卡洛模擬可能更有用。

Let’s lower a (our skew parameter) down to -2 and see what happens.

讓我們將 (我們的偏斜參數)降低到-2，看看會發生什么。

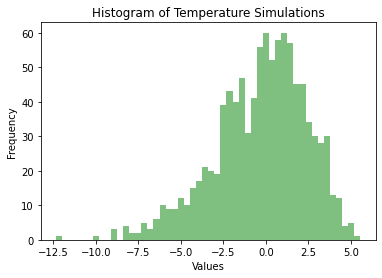
A minimum mean monthly temperature of -12.34°C is recorded. This is still much higher than the minimum daily temperature recorded.

記錄的最低平均每月溫度為-12.34°C。 這仍然遠高于記錄的最低每日溫度。

In this regard, while a Monte Carlo simulation was useful for modelling monthly data — such a simulation still cannot compensate for a scenario where we do not have the data we want.

在這方面，雖然蒙特卡洛模擬對于建模月度數據很有用，但這種模擬仍無法彌補我們沒有所需數據的情況。

The likelihood is that taking daily temperature data for Braemar would mean a much more negatively skewed distribution. That said, the mean and standard deviation of that series would also likely vary significantly — without knowledge of these parameters then the Monte Carlo Simulation is limited in terms of being able to estimate daily values.

可能是，獲取Braemar的每日溫度數據將意味著分布出現更大的負偏斜。 就是說，該系列的平均值和標準偏差也可能會發生很大變化-如果不了解這些參數，則蒙特卡洛模擬在能夠估計每日值方面受到限制。

A Monte Carlo simulation can be strong when we have the right data — but it does not necessarily make up for a lack of data.

當我們擁有正確的數據時，蒙特卡洛模擬可能會很強大，但不一定能彌補數據的不足。

結論 (Conclusion)

This has been an introduction to how a Monte Carlo simulation can be used to model extreme weather events.

這是對如何使用蒙特卡洛模擬法對極端天氣事件進行建模的介紹。

In particular, we saw:

特別是，我們看到了：

• The importance of identifying the correct distribution for the time series in question
  確定有關時間序列的正確分布的重要性

• Use of skewnorm in scipy for generating random numbers with a defined skew

  在scipy中使用skewnorm生成具有定義的偏斜的隨機數

• Implementation of a Monte Carlo simulation for identifying extreme potential values
  實施蒙特卡羅模擬以識別極高的潛在價值

Many thanks for your time, and any questions or feedback are greatly appreciated. You can find the GitHub repository for this example here.

非常感謝您的寶貴時間，任何問題或反饋都將不勝感激。 您可以在此處找到此示例的GitHub存儲庫。

Disclaimer: This article is written on an “as is” basis and without warranty. It was written with the intention of providing an overview of data science concepts, and should not be interpreted as professional advice in any way. The findings and interpretations in this article are those of the author and are not endorsed by or affiliated with the UK Met Office in any way.

免責聲明：本文按“原樣”撰寫，不作任何擔保。 它旨在提供數據科學概念的概述，并且不應以任何方式解釋為專業建議。 本文中的發現和解釋僅歸作者所有，并不以任何方式得到英國氣象局的認可或附屬。