邏輯回歸 (Logistic Regression)
目前最流行,使用最廣泛的一種學習算法。
分類問題,要預測的變量 y 是離散的值。
邏輯回歸算法的性質是:它的輸出值永遠在 0 到 1 之間。
邏輯回歸模型的假設是:
其中:
X 代表特征向量
g 代表logistic function,是一個常用的Sigmoid function。
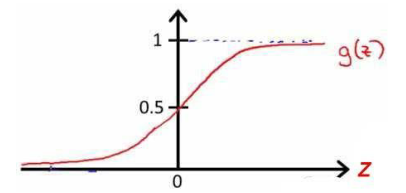
Sigmoid function:一個良好的閾值函數
導數:f'(x)=f(x)*[1-f(x)]
公式為:
圖像為:
合起來,得到Logistic回歸模型的假設:
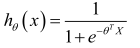
對于給定的輸入變量,根據選擇的參數計算輸出變量=1 的可能性(estimated probablity):
即
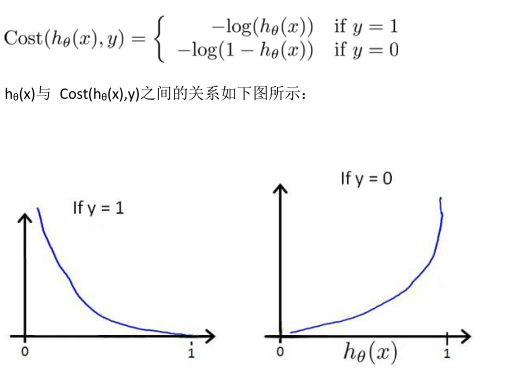
代價函數:
整理得:
帶入到代價函數(凸函數):
得到代價函數后, 便可以用梯度下降算法來求得能使代價函數最小的參數了。
算法為:
注:?
1、雖然得到的梯度下降算法表面上看上去與線性回歸的梯度下降算法一樣, 但是這里的 hθ(x)=g(θTX)與線性回歸不同,
所以實際上是不一樣的。
2、在運行梯度下降算法之前,進行特征縮放依舊是非常必要的。?
邏輯回歸,這是一種非常強大,甚至可能世界上使用最廣泛的一種分類算法。?
————————————————————————————————————————————————————————
高級優化(Advanced Optimization)
梯度下降并不是我們可以使用的唯一算法,還有其他一些算法,更高級、更復雜。
共軛梯度法 BFGS (變尺度法) 和 L-BFGS (限制變尺度法) 就是其中一些更高級的優化算法。
它們需要有一種方法來計算 J(θ),以及需要一種方法計算導數項, 然后使用比梯度下降更復雜的算法來最小化代價函數。?
這些算法的具體細節超出了本門課程的范疇。
實際上你最后通常會花費很多天,或幾周時間研究這些算法,你可以專門學一門課來提高數值計算能力。
這些算法有許多優點:?一個是使用這其中任何一個算法, 你通常不需要手動選擇學習率 α。
實際上, 我過去使用這些算法已經很長一段時間了, 也許超過十年了, 使用得相當頻繁。
而直到幾年前我才真正搞清楚共軛梯度法 BFGS 和 L-BFGS 的細節。?
我們實際上完全有可能成功使用這些算法, 并應用于許多不同的學習問題, 而不需要真正理解這些算法的內環間在做什么。
?如果說這些算法有缺點的話, 那么我想說主要缺點是它們比梯度下降法復雜多了。
特別是你最好不要使用 L-BGFS、 BFGS 這些算法, 除非你是數值計算方面的專家。
實際上,我不會建議你們編寫自己的代碼來計算數據的平方根,或者計算逆矩陣。
因為對于這些算法,我還是會建議你直接使用一個軟件庫。
比如說,要求一個平方根, 我們所能做的就是調用一些別人已經寫好用來計算數字平方根的函數。?
幸運的是現在我們有 Octave 和與它密切相關的 MATLAB 語言可以使用。?
所以當我有一個很大的機器學習問題時,我會選擇這些高級算法,而不是梯度下降。
有了這些概念, 你就應該能將邏輯回歸和線性回歸應用于更大的問題中, 這就是高級優化的概念。?
————————————————————————————————————————————————————————
(Multiclass Classification_ One-vs-all)
有幾類,就訓練幾個分類器。
預測時,將所有的分類機都運行一遍,選擇最高可能性。
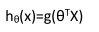
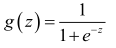
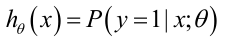

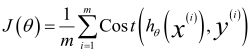
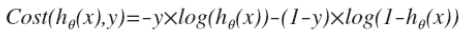
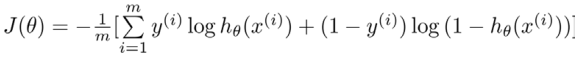
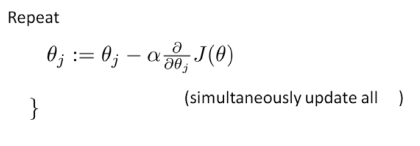
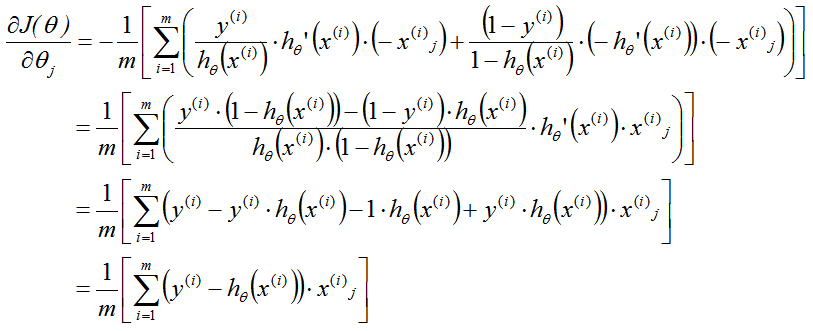





)

又稱為邏輯回歸分析,是分類和預測算法中的一種。通過歷史數據的表現對未來結果發生的概率進行預測。例如,我們可以將購買的概率設置為因變量,將用戶的)







)
--接口測試工具介紹(詳解))


