?什么是導數

　　導數是高數中的重要概念，被應用于多種學科。

　　從物理意義上講，導數就是求解變化率的問題；從幾何意義上講，導數就是求函數在某一點上的切線的斜率。

　　我們熟知的速度公式：v = s/t，這求解的是平均速度，實際上往往需要知道瞬時速度：

　　當t趨近于t₀，即t-t₀趨近于0時，得到的就是順時速度。設Δt=t-t₀，s是t的函數s=f(t)，瞬時速度用數學表示就是：

　　為什么s=f(t)呢？請看下圖：

　　將橫軸作為距離，以時間為單位分隔，在t₀時間經過的距離是f(t₀)=S₀，在t時間經過的距離是f(t)=s

　　在幾何上，如下圖所示：

　　直線a與曲線相切于點Q，直線b與曲線相割于點Q和點P。b的斜率，k=(y-y₀)/(x-x₀)，當b以Q為軸心沿著曲線旋轉時，鉉長|PQ|趨近于0，即x->x₀時，極限存在：

　　有上述兩個問題可以看出，變化率和切線的問題都可以歸結為下面的公式：

　　定義Δx = x-x₀, Δy = y - y0 = f(x) – f(x₀) = f(x₀?+ Δx) - f(x₀)，上面的公式可以寫成：

　　由此得出導數的概念，設函數y=f(x)在點x₀的某個鄰域內有定義，當自變量x在x₀處取得增量Δx（點x0+Δx仍在該鄰域內）時，相應地函數y取得增量Δy；如果Δy與Δx之比當Δx->0時的極限存在，則稱函數y=f(x)在點x₀處可導，并稱這個極限為函數y=f(x)在點x₀處的導數，記作f’(x₀)?：

　　也記作：

　　簡寫為：

1/x求導

　　根據導數公式，代入f(x) = 1/x

　　這就OK了，所以說導數很簡單，因為它僅有一個公式，但沒完，因為上式沒有任何意義，僅僅是看起來更復雜了。如果我們直接觀察導數公式，對于所有求導，當Δx->0時，分母為0，所以必須將導數進一步簡化。

　　需要注意的是，求f’(x)的完整說法是求f(x)在定義域某一點的導數，所以x是已知的，求某一點的導數，當然要知道這個點是什么。

求切線所在三角形的面積

　　如下圖所示，直線MN是曲線1/x的切線，切點是(x0,y0)，求S_△MON

　　S_△MON?= 1/2(MO * ON)，已知條件是切點(x₀,y₀)，需要求解的未知條件是MO和NO。

　　直線MN的公式是y=kx+b，根據上節的介紹，1/x在（x₀,y₀）的導數是MN的斜率 -1/x₀²，代入得：

　　y₀=-1/x₀^2?+ b ??=>

　　?1/x_0?= (-1/x₀²) x₀+ b? =>

　　? b = 2/x₀

　　設N點的坐標是(x,0)，代入y=kx+b得：

?????? 0=(-1/x₀²)x+2/x_0??=> x = 2x₀

　　即OM = 2x₀

　　同理，MO=2y₀

　　S_△MON?= 1/2(MO * ON) = 1/2(2x₀2y₀) = 1/2(2x₀)(2/x₀) = 2

冪函數求導

　　f(x) = Xⁿ的導數：f’(x) = nx^n-1

　　例：(3x⁶)’ = 3 * 6x^6-1?= ?18x⁵

　　該公式可以擴展到多項式中：

　　(3x³?+ 6x¹⁰)' = 3 * 3x^3-1?+ 6 * 10 x^10-1?= 9x²?+ 60x⁹

sin和cos求導

　　下面是sinx和cosx的去曲線圖：

sinx

cosx

　　sin0°= 0，sin90°= sin(π/2) = 1

　　求導時需要用到幾個公式：

　　1、2不解釋，3、4后面會給出證明：

(sinx)’

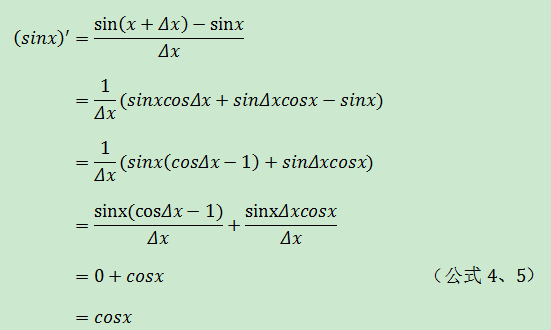
(cosx)’

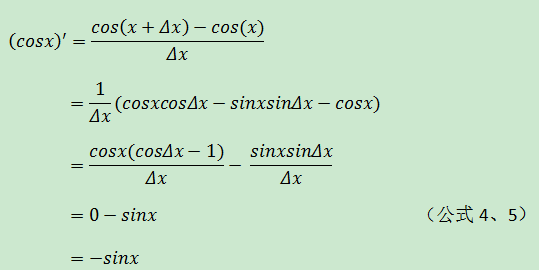
為什么會有公式3、4

　　，需要從幾何意義上證明。

　　上圖是一個單位圓，將Δx用θ替換。由于單位圓r=1，弧長MN=(2πr ) (θ/360) = (2πr)(θ/2π) =θ。

　　公式3：

　　當θ趨近于0時，PN比弧長MN更快地趨近于0，所以公式3成立。

　　公式4：sinθ=MP/OM=MP. 當θ趨近于0時，MP越來越趨近與MN（趨近但不等于0），所以

函數可導的條件

　　如果一個函數的定義域為全體實數，即函數在其上都有定義，那么該函數是不是在定義域上處處可導呢？答案是否定的。函數在定義域中一點可導需要一定的條件：函數在該點的左右兩側導數都存在且相等。這實際上是按照極限存在的一個充要條件（極限存在，它的左右極限存在且相等）推導而來。

　　可導的函數一定連續；連續的函數不一定可導，不連續的函數一定不可導。

　　下面是兩個不可導的例子：

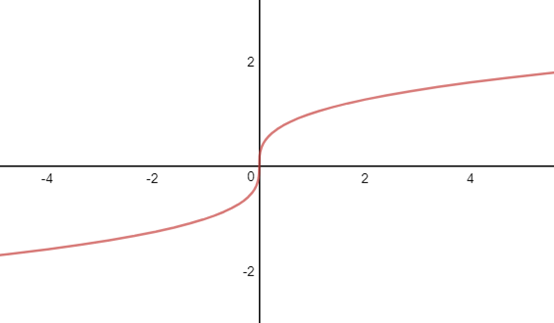
f(x)=x^1/3

　　f(x)=x^1/3，f’(x)=x^-2/3/3在x=0處分母為0，所以在x=0處不可導。實際上該函數在x=0處的切線是y軸，導數趨近于無窮，不符合導數的定義。

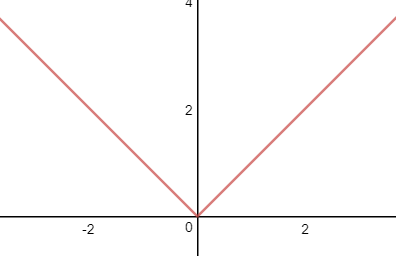
f(x)=|x|

　　幾何上，切線指的是一條剛好觸碰到曲線上某一點的直線。更準確地說，當切線經過曲線上的某點（即切點）時，切線的方向與曲線上該點的方向是相同的。f(x)=|x|在x=0點時，曲線沒有唯一方向，即在x=0點沒有切線，所以該函數在x=0點不可導。

總結

1. 導數的物理意義：描述變化率，幾何意義：切線的斜率
2. 導數公式:
3. 基本函數求導公式

1)?????? (C)’ = 0

2)?????? (1/x)’ = -1/x²

3)?????? (xⁿ)’ = nx^n-1

4)?????? (sinx)’ = cosx

5)?????? (cosx)’=-sinx

　　4.可導的充要條件，它的左右極限存在且相等；可導的函數一定連續；連續的函數不一定可導，不連續的函數一定不可導。