正則化(Regularization)
過擬合問題(Overfitting):
如果有非常多的特征,通過學習得到的假設可能能夠非常好地適應訓練集 :代價函數可能幾乎為 0),
但是可能會不能推廣到新的數據。
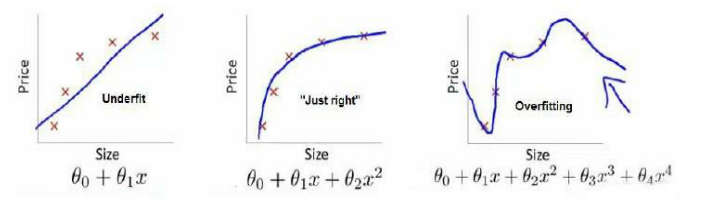
第一個模型是一個線性模型,欠擬合,不能很好地適應我們的訓練集;
第三個模型是一個四次方的模型,過于強調擬合原始數據,而丟失了算法的本質:預測新數據。
我們可以看出,若給出一個新的值使之預測,它將表現的很差,是過擬合,
雖然能非常好地適應我們的訓練集但在新輸入變量進行預測時可能會效果不好;而中間的模型似乎最合適。?
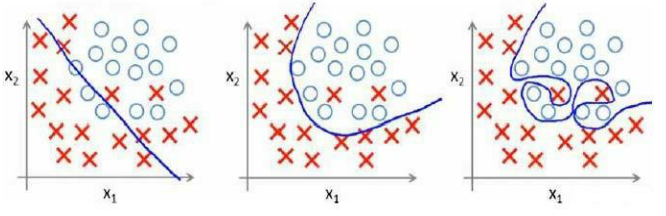
分類問題中也存在這樣的問題:
就以多項式理解,x 的次數越高,擬合的越好,但相應的預測的能力就可能變差。?
問題是,如果我們發現了過擬合問題,應該如何處理??
1. 丟棄一些不能幫助我們正確預測的特征。可以是手工選擇保留哪些特征,或者使用一些模型選擇的算法來幫忙(例如 PCA)。?
2. 正則化。 保留所有的特征,但是減少參數的大小(magnitude)。?
————————————————————————————————————————————————————————
代價函數:
上面的回歸問題中如果我們的模型是:?
我們可以從之前的事例中看出, 正是那些高次項導致了過擬合的產生。
所以如果能讓這些高次項的系數接近于 0 的話,我們就能很好的擬合了。
所以我們要做的就是在一定程度上減小這些參數 θ 的值, 這就是正則化的基本方法。?
我們決定要減少 θ3 和 θ4 的大小,我們要做的便是修改代價函數,在其中 θ3和 θ4 設置一點懲罰。
這樣做的話,我們在嘗試最小化代價時也需要將這個懲罰納入考慮中,并最終導致選擇較小一些的 θ3 和 θ4。
修改后的代價函數如下:?
通過這樣的代價函數選擇出的 θ3和 θ4對預測結果的影響就比之前要小許多。
假如我們有非常多的特征,我們并不知道其中哪些特征我們要懲罰。
我們將對所有的特征進行懲罰,并且讓算法自動來選擇這些懲罰的程度。
這樣的結果是得到了一個較為簡單的能防止過擬合問題的假設:?
其中 λ 又稱為正則化參數(Regularization Parameter)。
注:根據慣例,我們不對 θ0 進行懲罰。
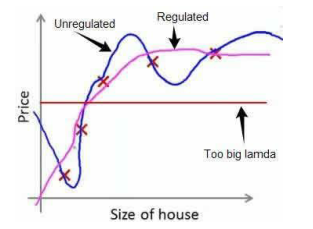
經過正則化處理的模型與原模型的可能對比如下圖所示:
如果選擇的正則化參數 λ 過大,則會把所有的參數都最小化了,導致模型變成 hθ(x)=θ0 。
也就是上圖中紅色直線所示的情況,造成欠擬合。?
因為如果我們令λ的值很大的話, 為了使 Cost Function 盡可能的小, 所有的 θ 的值 (不包括 θ0)都會在一定程度上減小。?
但若λ的值太大了,那么 θ(不包括 θ0)都會趨近于 0,這樣我們所得到的只能是一條平行于 x 軸的直線。?
所以對于正則化,我們要取一個合理的λ的值,這樣才能更好的應用正則化。?
回顧一下代價函數, 為了使用正則化, 讓我們把這些概念應用到線性回歸和邏輯回歸中去,那么我們就可以讓他們避免過度擬合了。
—————————————————————————————————————————————————————————
正則化線性回歸(Regularized Linear Regression)
隨機梯度下降:
正規方程:
—————————————————————————————————————————————————————————
正則化Logistic回歸(Regularized Logistic Regression)
注意:
1、雖然正則化的邏輯回歸中的梯度下降和正則化的線性回歸中的表達式看起來一樣,但由于兩者h(x)不同,所以差別很大。
2、 θ0不參與其中的任何一個正則化。
—————————————————————————————————————————————————————————————————————————————
小結:
目前大家對機器學習算法可能還只是略懂, 但是一旦你精通了線性回歸、Logistic回歸、高級優化算法和正則化技術,
坦率地說,你對機器學習的理解可能已經比許多工程師深入了。
現在,你已經有了豐富的機器學習知識, 目測比那些硅谷工程師還厲害, 或者用機器學習算法來做產品。 ?
接下來的課程中,我們將學習一個非常強大的非線性分類器,無論是線性回歸,還是Logistic回歸,都可以構造多項式來解決。
你將逐漸發現還有更強大的非線性分類器,可以用來解決多項式回歸問題。
我們接下來將將學會,比現在解決問題的方法強大 N 倍的學習算法。?
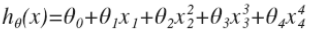
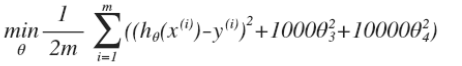
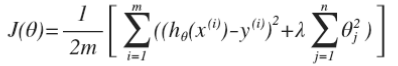
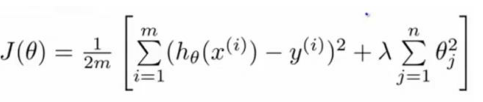
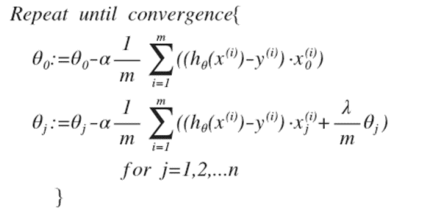
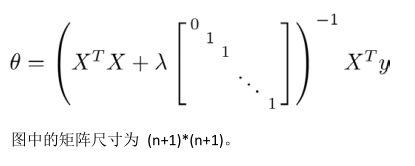
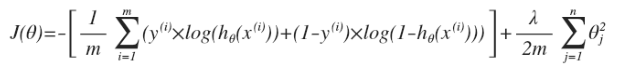
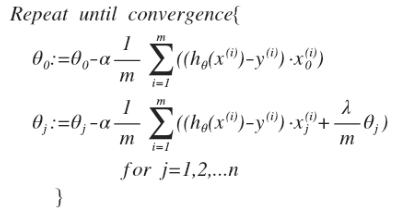

)

又稱為邏輯回歸分析,是分類和預測算法中的一種。通過歷史數據的表現對未來結果發生的概率進行預測。例如,我們可以將購買的概率設置為因變量,將用戶的)







)
--接口測試工具介紹(詳解))




)

)