神經網絡:表示(Neural Networks: Representation)
如今的神經網絡對于許多應用來說是最先進的技術。
對于現代機器學習應用,它是最有效的技術方法。
神經網絡模型是許多邏輯單元按照不同層級組織起來的網絡, 每一層的輸出變量都是下一層的輸入變量。
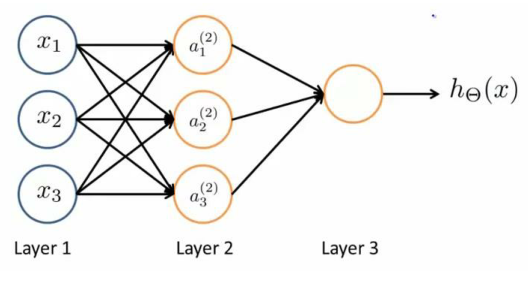
下圖為一個 3 層的神經網絡:
第一層為輸入層(Input Layer)
中間一層為隱藏層(Hidden Layers)
最后一層為輸出層(Output Layer)
我們為每一層都增加一個偏差單位(bias unit):
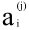
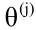
其尺寸為:以第 j+1 層的激活單元數量為行數,以第 j 層的激活單元數加1為列數的矩陣。
對于上圖所示的模型,激活單元和輸出分別表達為:
每一個 a 都是由上一層所有的 x 和每一個 x 所對應的權重決定的。
把這樣從左到右的算法稱為前向傳播算法( FORWARD PROPAGATION )
完整計算過程:
其實神經網絡就像是 logistic regression,只不過我們把 logistic regression 中的輸入向量[x1~x3]變成了中間層的[a(2)1~a(2)3]。
我們可以把 a0,a1,a2,a3看成更為高級的特征值,也就是 x0,x1,x2,x3的進化體,并且它們是由 x 與決定的。
這些更高級的特征值遠比 x 次方厲害,也能更好的預測新數據。?
這就是神經網絡相比于邏輯回歸和線性回歸的優勢。?
—————————————————————————————————————————————————————————
從本質上講,神經網絡能夠通過學習得出其自身的一系列特征。
神經網絡中,單層神經元(無中間層)的計算可用來表示邏輯運算,比如邏輯 AND、邏輯或 OR 、邏輯非NOT。?
可以利用神經元來組合成更為復雜的神經網絡以實現更復雜的運算, 例如?XNOR 功能。
按這種方法我們可以逐漸構造出越來越復雜的函數,也能得到更加厲害的特征值。?
這就是神經網絡的厲害之處。
—————————————————————————————————————————————————————————
假設k類,則輸出層有k個神經元。
每個樣例的類標都是一個k向量,對應下標置1,其余置0。
如有4類:
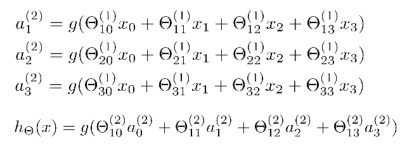


又稱為邏輯回歸分析,是分類和預測算法中的一種。通過歷史數據的表現對未來結果發生的概率進行預測。例如,我們可以將購買的概率設置為因變量,將用戶的)







)
--接口測試工具介紹(詳解))




)

)
 用于數據可視化實驗 -- Matlab版)

