無監督學習

在非監督學習中，我們需要將一系列無標簽的訓練數據，輸入到一個算法中， 然后讓它找這個數據的內在結構。

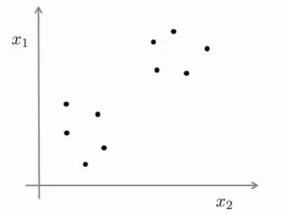
?我們可能需要某種算法幫助我們尋找一種結構。圖上的數據看起來可以分成兩個分開的點集（稱為簇），一個能夠找到我圈出的這些點集的算法，就被稱為聚類算法。

這將是我們介紹的第一個非監督學習算法。?

當然， 此后還將提到其他類型的非監督學習算法，它們可以找到其他類型的結構或者其他的一些模式，而不只是簇。?

那么聚類算法一般用來做什么呢？

應用例子：

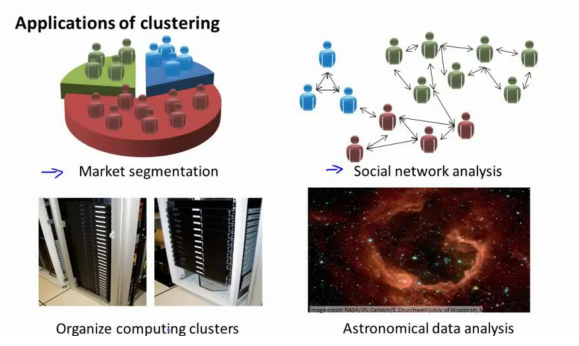
1、市場分割：也許你在數據庫中存儲了許多客戶的信息，而你希望將他們分成不同的客戶群，這樣你可以對不同類型的客戶分別銷售產品或者分別提供更適合的服務。

2、社交網絡分析： 事實上有許多研究人員正在研究這樣一些內容，他們關注一群人，關注社交網絡，例如 Facebook， Google+，或者是其他的一些信息，比如說：你經常跟哪些人聯系，而這些人又經常給哪些人發郵件，由此找到關系密切的人群。 因此， 這可能需要另一個聚類算法， 你希望用它發現社交網絡中關系密切的朋友。

3、用聚類算法來更好的組織計算機集群， 或者更好的管理數據中心。因為如果你知道數據中心中，哪些計算機經常協作工作。那么，你可以重新分配資源，重新布局網絡。由此優化數據中心，優化數據通信。?

4、研究如何利用聚類算法了解星系的形成。然后用這個知識，了解一些天文學上的細節問題。?

—————————————————————————————————————————————————————————

K-均值算法（K-Means Algorithm）

K-均值是最普及的聚類算法，算法接受一個未標記的數據集，然后將數據聚類成不同的組。?

K-均值是一個迭代算法，假設我們想要將數據聚類成 n 個組，其方法為:?

1、首先選擇 K 個隨機的點，稱為聚類中心（cluster centroids）；?

2、對于數據集中的每一個數據， 按照距離 K 個中心點的距離， 將其與距離最近的中心點關聯起來，與同一個中心點關聯的所有點聚成一類。?

3、計算每一個組的平均值，將該組所關聯的中心點移動到平均值的位置。?

4、重復步驟 2-3 直至中心點不再變化。

K-均值算法也可以很便利地用于將數據分為許多不同組， 即使在沒有非常明顯區分組群的情況下也可以。

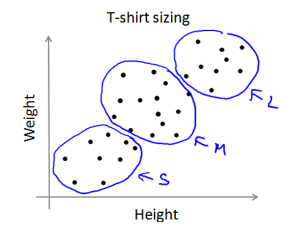
下圖所示的數據集包含身高和體重兩項特征構成的， 利用 K-均值算法將數據分為三類，用于幫助確定將要生產的 T-恤衫的三種尺寸。

—————————————————————————————————————————————————————————

優化目標（Optimization Objective）

K-均值最小化問題，是要最小化所有的數據點與其所關聯的聚類中心點之間的距離之和。

因此 K-均值的代價函數（又稱畸變函數 Distortion function）為：?

—————————————————————————————————————————————————————————

隨機初始化（Random Initialization）

在運行 K-均值算法的之前，我們首先要隨機初始化所有的聚類中心點：?

1.?應該選擇 K<m，即聚類中心點的個數要小于所有訓練集實例的數量；

2.?隨機選擇 K 個訓練實例，然后令 K 個聚類中心分別與這 K 個訓練實例相等。

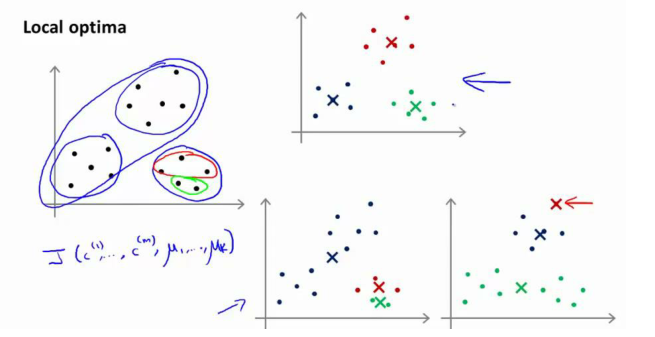
K-均值的一個問題在于，它有可能會停留在一個局部最小值處，而這取決于初始化的情況。?

為了解決這個問題，通常需要多次運行 K-均值算法，每一次都重新進行隨機初始化，最后再比較多次運行 K-均值的結果，選擇代價函數最小的結果。

這種方法在 K 較小的時候（2--10）還是可行的，但是如果 K 較大，這么做也可能不會有明顯地改善。

—————————————————————————————————————————————————————————

選擇聚類數（Choosing the Number of Clusters）

沒有所謂最好的選擇聚類數的方法，通常是需要根據不同的問題，人工進行選擇。

選擇的時候思考我們運用 K-均值算法聚類的動機是什么，然后選擇能最好服務于該目的標聚類數。

比如，我們的 T-恤制造例子中，我們要將用戶按照身材聚類，我們可以分成 3 個尺寸?S,M,L；也可以分成 5 個尺寸 XS,S,M,L,XL。這樣的選擇是建立在回答“聚類后我們制造的 T-恤是否能較好地適合我們的客戶”這個問題的基礎上作出的。

另一種方法是肘部法則：

關于“肘部法則”，我們所需要做的是改變 K 值，也就是聚類類別數目的總數。

我們用一個聚類來運行 K 均值聚類方法然后計算畸變函數 J。

我們可能會得到一條類似于這樣的曲線，像一個人的肘部。?

讓我們來看這樣一個圖，看起來就好像有一個很清楚的肘在那兒。好像人的手臂，如果你伸出你的胳膊，那么這就是你的肩關節、肘關節、手。這就是“肘部法則”。

你會發現這種模式，從 1 到 2，從 2 到 3，它的畸變值會迅速下降。之后，會在 3 的時候達到一個肘點，在此之后，畸變值就下降的非常慢，看起來就像使用 3 個聚類來進行聚類是正確的，這是因為那個點是曲線的肘點。K等于3之前畸變值下降得很快，K 等于 3 之后就下降得很慢，那么我們就選 K 等于 3。當你應用“肘部法則”的時候，如果你得到了一個像上面這樣的圖，那么這將是一種
用來選擇聚類個數的合理方法。?