支持向量機(Support Vector Machines)
在監督學習中,許多學習算法的性能都非常類似,因此,重要的不是你該選擇使用學習算法 A 還是學習算法 B,而更重要的是,
應用這些算法時,所創建的大量數據在應用這些算法時,表現情況通常依賴于你的水平。
比如:你為學習算法所設計的特征量的選擇,以及如何選擇正則化參數,諸如此類的事。
還有一個更加強大的算法廣泛的應用于工業界和學術界,它被稱為支持向量機(Support Vector?Machine)。
與邏輯回歸和神經網絡相比,支持向量機,或者簡稱 SVM,在學習復雜的非線性方程時提供了一種更為清晰,更加強大的方式。
與Logistics回歸成本函數的不同:
1、刪去常量?1/m ;
2、Logistic:A+λ×B,SVM:?C×A+B。如果給定λ一個非常大的值,意味著給予 B 更大的權重。而這里,就對應于將 C 設定為非常小的值,那么,相應的將會給 B 比給 A 更大的權重。因此,這只是一種不同的方式來控制這種權衡或者一種不同的方法, 即用參數來決定是更關心第一項的優化, 還是更關心第二項的優化。當然你也可以把這里的參數 C 考慮成 1/λ,同 1/λ 所扮演的角色相同。
3、Logistic輸出概率,SVM直接預測y的值為0還是1。
?成本函數:
接下來會考慮一個特例:將常數 C 設置成一個非常大的值。
比如假設 C 的值為100000 或者其它非常大的數,然后來觀察支持向量機會給出什么結果?
如果 C 非常大,則最小化代價函數的時候,我們將會很希望找到一個使第一項為 0 的最優解。即不希望出現分錯的點,相當于過擬合。
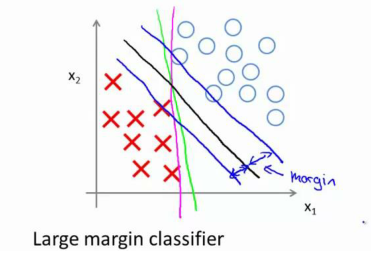
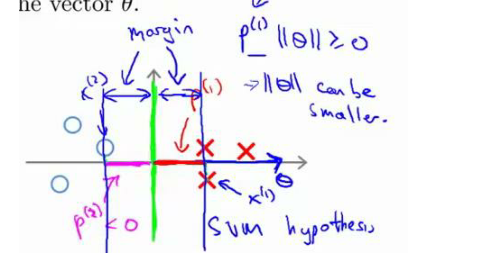
此時,兩類點完全分類正確。黑線有更大的距離,這個距離叫做間距 (margin)。?
當畫出這兩條額外的藍線,看到黑色的決策界和訓練樣本之間有更大的最短距離。然而粉線和藍線離訓練樣本就非常近,在分離樣本的時候就會比黑線表現差。因此,這個距離叫做支持向量機的間距, 而這是支持向量機具有魯棒性的原因, 因為它努力用一個最大間距來分離樣本。 因此支持向量機有時被稱為大間距分類器,。
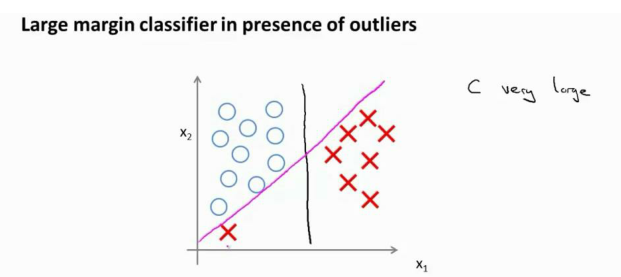
將這個大間距分類器中的正則化因子常數 C 設置的非常大,我記得我將其設置為了 100000,因此對這樣的一個數據集,也許我們將選擇這樣的決策界,從而最大間距地分離開正樣本和負樣本。 那么在讓代價函數最小化的過程中,我們希望找出在 y=1 和 y=0 兩種情況下都使得代價函數中左邊的這一項盡量為零的參數。如果我們找到了這 樣的參數,則我們的最小化問題便轉變成:?
事實上, 支持向量機現在要比這個大間距分類器所體現得更成熟。
?尤其是當你使用大間距分類器的時候,你的學習算法會受異常點 (outlier) 的影響。
在這里,如果你加了這個樣本,為了將樣本用最大間距分開,也許我最終會得到這條粉色的線,僅僅基于一個異常值就將決策界從這條黑線變到這條粉線,這實在是不明智的。而如果正則化參數 C,設置的非常大,這事實上正是支持向量機將會做的。
但是如果 C?設置的小一點,則你最終會得到這條黑線。
因此,大間距分類器的描述,僅僅是從直觀上給出了正則化參數 C 非常大的情形,同時,要提醒你 C 的作用類似于 1/λ,λ是我們之前使用過的正則化參數。這只是C 非常大的情形,或者等價地λ非常小的情形。你最終會得到類似粉線這樣的決策界,但是實際上應用支持向量機的時候,當 C 不是非常非常大的時候,它可以忽略掉一些異常點的影響,得到更好的決策界。甚至當你的數據不是線性可分的時候,支持向量機也可以給出好的結果。?
回顧 C=1/λ,因此:?
C 較大時,相當于 λ 較小,可能會導致過擬合,高方差。?
C 較小時,相當于 λ 較大,可能會導致低擬合,高偏差。?
這節課給出了一些關于為什么支持向量機被看做大間距分類器的直觀理解。它用最大間距將樣本區分開,盡管從技術上講,這只有當參數 C 是非常大的時候是真的,但是它對于理解支持向量機是有益的。?
—————————————————————————————————————————————————————————
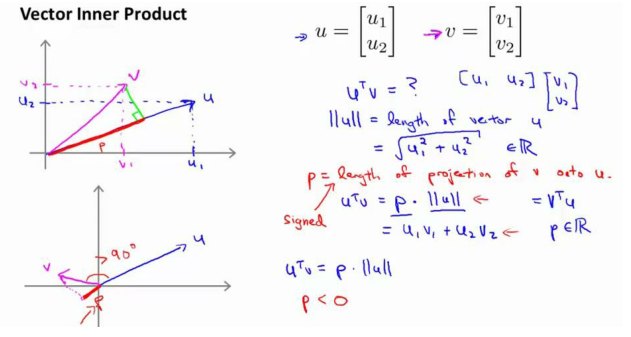
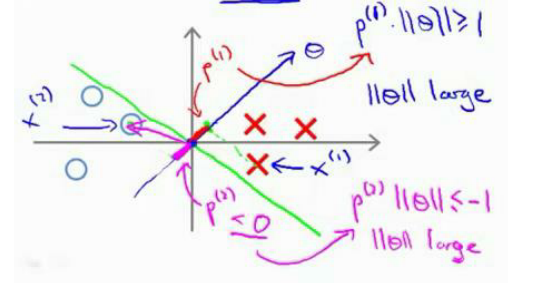
?Mathematics Behind Large Margin Classification
—————————————————————————————————————————————————————————————————————————————
核函數
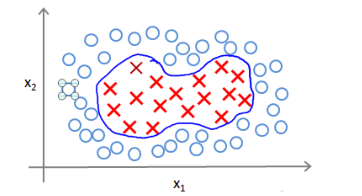
回顧我們之前討論過可以使用高級數的多項式模型來解決無法用直線進行分隔的分類問題:
為了獲得上圖所示的判定邊界,我們的模型可能是:
可以用一系列的新的特征 f 來替換模型中的每一項。例如令:
得到 hθ(x)=f1+f2+...+fn。
然而,除了對原有的特征進行組合以外,有沒有更好的方法來構造 f1,f2,f3?
可以利用核函數來計算出新的特征。
這里是一個高斯核函數(Gaussian?Kernel)。?
注:這個函數與正態分布沒什么實際上的關系,只是看上去像而已。
如果使用高斯核函數,那么在使用之前進行特征縮放是非常必要的。?
另外, 支持向量機也可以不使用核函數, 不使用核函數又稱為線性核函數 (linear kernel)。?
當不采用非常復雜的函數, 或者訓練集特征非常多而實例非常少的時候, 可以采用這種不帶核函數的支持向量機。
?
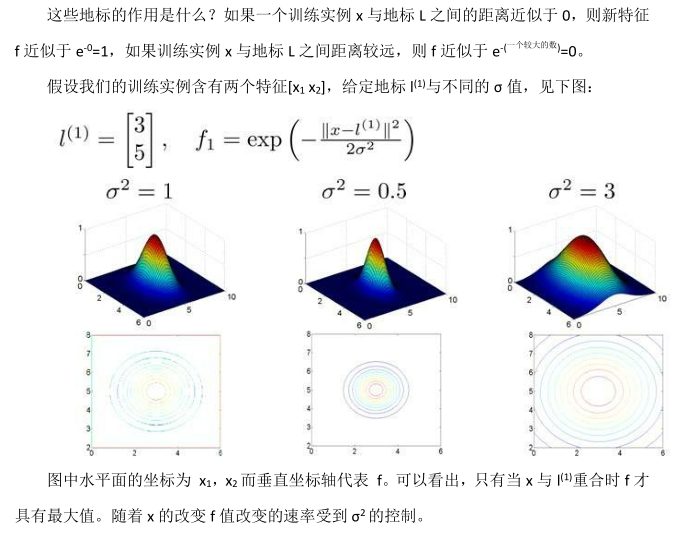
支持向量機的兩個參數 C 和 σ 的影響:?
C 較大時,相當于 λ 較小,可能會導致過擬合,高方差;?
C 較小時,相當于 λ 較大,可能會導致低擬合,高偏差;?
σ 較大時,導致高方差;?
σ 較小時,導致高偏差。
—————————————————————————————————————————————————————————
使用支持向量機
強烈建議使用高優化軟件庫中的一個, 而不是嘗試自己落實一些數據。
有許多好的軟件庫,我正好用得最多的兩個是 liblinear 和 libsvm。
在高斯核函數之外我們還有其他一些選擇,如:?
多項式核函數(Polynomial Kernel)?
字符串核函數(String kernel)?
卡方核函數( chi-square kernel)?
直方圖交集核函數(histogram intersection kernel)?
等等... ?
這些核函數的目標也都是根據訓練集和地標之間的距離來構建新特征。
這些核函數需要滿足 Mercer's 定理,才能被支持向量機的優化軟件正確處理。
多類分類問題?
假設我們利用之前介紹的一對多方法來解決一個多類分類問題。 如果一共有 k 個類, 則我們需要 k 個模型,以及 k 個參數向量 θ。我們同樣也可以訓練 k 個支持向量機來解決多類分類問題。 但是大多數支持向量機軟件包都有內置的多類分類功能, 我們只要直接使用即可。 ?
盡管你不去寫你自己的 SVM(支持向量機)的優化軟件,但是你也需要做幾件事:?
1、是提出參數 C 的選擇。即誤差/方差在這方面的性質。?
2、你也需要選擇內核參數或你想要使用的相似函數,其中一個選擇是:選擇不需要任何內核參數,沒有內核參數的理念,也叫線性核函數。因此,如果有人說他使用了線性核的 SVM(支持向量機),這就意味這他使用了不帶有核函數的 SVM(支持向量機)。?
Logistics和SVM該如何選擇:
下面是一些普遍使用的準則:?
m 為訓練樣本數,n 為特征數。?
(1)如果相較于 m 而言,n 要大許多,即訓練集數據量不夠支持我們訓練一個復雜的非線性模型,我們選用邏輯回歸模型或者不帶核函數的支持向量機。?
(2)如果 n 較小,而且 m 大小中等,例如 n 在 1-1000 之間,而 m 在 10-10000 之間,使用高斯核函數的支持向量機。?
(3)如果 n 較小,而 m 較大,例如 n 在 1-1000 之間,而 m 大于 50000,則使用支持向量機會非常慢,解決方案是創造、增加更多的特征,然后使用邏輯回歸或不帶核函數的支持向量機。?
邏輯回歸和不帶核函數的支持向量機它們都是非常相似的算法, 不管是邏輯回歸還是不帶核函數的 SVM,通常都會做相似的事情,并給出相似的結果。
值得一提的是, 神經網絡在以上三種情況下都可能會有較好的表現, 但是訓練神經網絡可能非常慢,選擇支持向量機的原因主要在于它的代價函數是凸函數,不存在局部最小值。 ?
通常更加重要的是:你有多少數據,你有多熟練是否擅長做誤差分析和排除學習算法, 指出如何設定新的特征變量和找出其他能決定你學習算法的變量等方面,通常這些方面會比你使用邏輯回歸還是 SVM 這方面更加重要。

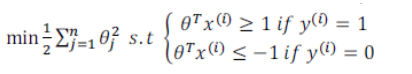

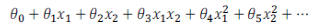
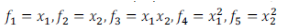

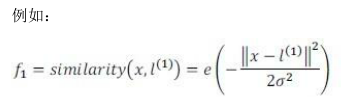




)

)
 用于數據可視化實驗 -- Matlab版)


)

)







