和、差、積、商求導法則

　　設u=u(x),v=v(x)都可導，則：

1. (Cu)’ = Cu’, C是常數
2. (u ± v)’ = u’ ± v’
3. (uv)’ = u’ + v’
4. (u/v)’ = (u’v – uv’) / v²

　　1、2不解釋，下面給出3、4的推導過程

乘法法則的推導過

?

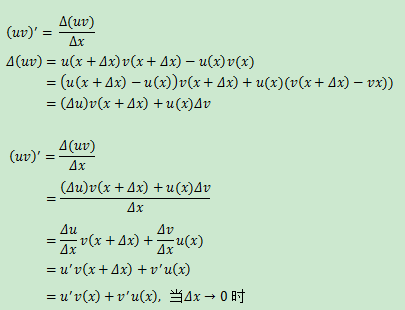　　乘法法則可擴展：

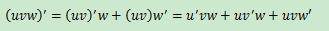
除法法則的推導過程

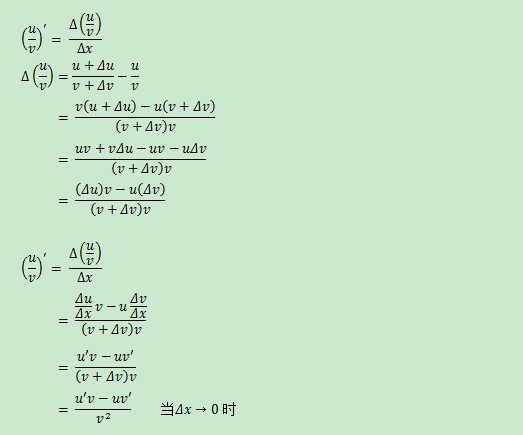
示例1：f'(1/x)

　　根據除法法則：

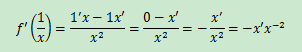
示例2：f'(x^-n)

　　根據除法法則：

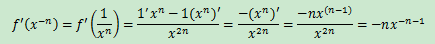
　　上式結果也可直接根據冪函數求導法則得出，冪函數f(x) = Xⁿ的導數：f’(x) = nx^n-1

示例3：（secx）’

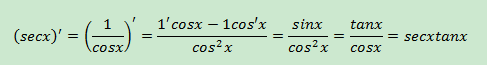
鏈式求導法則

　　鏈式求導法則也稱為復合函數求導法則。若u=g(x)在x點可導，y=f(u)在u=g(x)點可導，則y=f(g(x))在x點可導，其導數是：

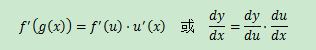
　　第二種寫法看起來更好理解。

示例1：y=(sinx)¹⁰求導

　　這是一個典型的符合函數，內部函數是u=sinx，外部函數是y=u¹⁰，根據公式：

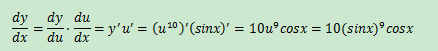
示例2：sin(10x)求導

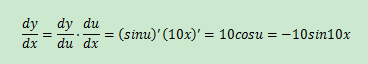
高階導數

　　高階導數實際上是對導數求導，也就是不斷求導。

　　二階導數表示為(u’)’=u’’；三階導數u’’’；四階導數不能再用撇號表示了，需要使用上標u⁽⁴⁾；n階導數u⁽ⁿ⁾。在訓練集中，上標也被表示為第幾組訓練集，在此我們看到，數學中的符號經常會被重用，在不同上下文中有不同的含義。

　　sinx的二階導數：(sinx)’’=(cosx)’=-sinx

　　高階導數也有不同的表示法，以三階導數為例：

　　看起來越來越亂了-_-|||

冪函數的高階導數

D¹xⁿ?= nx^n-1

D²xⁿ?= ( D¹xⁿ)’= (nx^n-1)’=n(x^n-1)’=n(n-1)(x^?n-2)

D³x^n?= (D²xⁿ)’ = n(n-1)(n-2)(x^n-3)

……

D^n-1xⁿ?= n(n-1)(n-2)(n-3)…(2)x¹

Dⁿxⁿ?= n(n-1)(n-2)(n-3)…(2)(1)x⁰?= n!

Dⁿ⁺¹xⁿ?= (n!)’ = 0

?

高階導數的意義

　　幾何意義比較容易理解，一階導數是切線的斜率，二階是斜率的變化率，三階是斜率的變化率的變化率……階數越高，刻畫的變化越精細。

　　物理意義是百度來的，用時間、距離、速度舉例：

　　位移相對于時間的一階導數是速度，二階導數是加速度，三階導數是急動度(加速度的的變化率)，四階導數是什么痙攣度(不知道是不是瞎編出來的，從這開始就理解不了了)……當一輛小車尾部遭受撞擊時，加速度會突然改變，小車具有急動度。汽車工程師用急動度作為評判乘客不舒適程度的指標；按照這一指標,具有恒定加速度和零急動度的人體感覺最舒適。在競技舉重中，舉重運動員進行所有將杠鈴舉過頭頂的動作時都有急動度。當輪船到達溪谷，突然減速時，輪船有急動度，因為輪船加速度的大小和方向都要改變。

總結

　　1.函數的和、差、積、商求導法則

　　1)???????? (Cu)’ = Cu’, C是常數

　　2)???????? (u ± v)’ = u’ ± v’

　　3)???????? (uv)’ = u’ + v’

　　4)???????? (u/v)’ = (u’v – uv’) / v²

　　2.鏈式求導法則（復合函數求導法則）

?

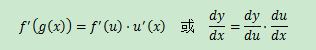
　　3.高階導數

　　對導數求導，u’’,u’’’,u(4)

　　Dⁿxⁿ?= n!

　　Dⁿ⁺¹xⁿ?= 0