降維(Dimensionality Reduction)?:
一、 降維目的:
目的一:數據壓縮(Data Compression)
目的二:數據可視化(Visualization)
二、 主成分分析(PCA)
主成分分析問題的描述:
算法:?
選擇主成分的數量,即k值:
壓縮后的復原:
三、 錯誤的應用場景:
?
降維(Dimensionality Reduction)?:
?
一、 降維目的:
目的一:數據壓縮(Data Compression)
數據壓縮不僅可以節省內存或磁盤,還可以加快學習算法。 ?
可以把任何維度的數據降到任何想要的維度, 例如將 1000 維的特征降至 100 維。
?
目的二:數據可視化(Visualization)
50 維的數據不能可視化,但將其降至 2 維,便可以將其可視化。
這樣做的問題在于,降維算法只負責減少維數,新特征的意義必須由我們自己去發現了。?
二、 主成分分析(PCA)
主成分分析(PCA)是最常見的降維算法。?
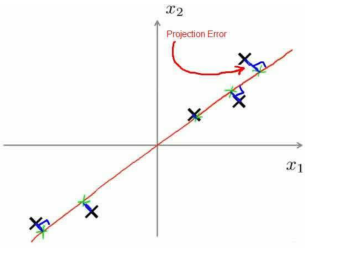
在 PCA 中,要做的是找到一個方向向量(Vector direction),當把所有的數據都投射到該向量上時,希望投射平均均方誤差能盡可能地小。方向向量是一個經過原點的向量,而投射誤差是從特征向量向該方向向量作垂線的長度。
?
主成分分析問題的描述:
將 n 維數據降至 k 維,目標是找到向量 u(1),u(2),...,u(k)使得總的投射誤差最小。
?
PCA 將 n 個特征降維到 k 個, 可以用來進行數據壓縮, 如果 100 維的向量最后可以用 10維來表示,那么壓縮率為 90%。
同樣圖像處理領域的 KL 變換使用 PCA 做圖像壓縮。但 PCA?要保證降維后,數據的特性損失最小。
?
PCA 技術的一大好處是對數據進行降維處理。我們可以對新求出的“主元” 向量的重要性進行排序,根據需要取前面最重要的部分,將后面的維數省去,可以達到簡化模型或是數據壓縮的效果。同時最大程度的保持了原有數據的信息。
?
PCA 技術的一個很大的優點是,它是完全無參數限制的。在 PCA 的計算過程中完全不需要人為設定參數或是根據任何經驗對計算進行干預, 最后的結果只與數據相關, 對用戶是獨立的。?
但是,這也可以看作是缺點。如果用戶對觀測對象有一定的先驗知識,掌握了數據的一些特征, 卻無法通過參數化等方法對處理過程進行干預, 可能會得不到預期的效果。
?
?
算法:?
1、均值歸一化;?
2、 計算矩陣;
3、計算矩陣? 的特征值和特征向量;
4、根據特征值排序,選出前k個對應的特征向量。
5、將每個樣例和k個特征向量做內積,即得到降維后的k個特征。
?
?
選擇主成分的數量,即k值:
?
壓縮后的復原:
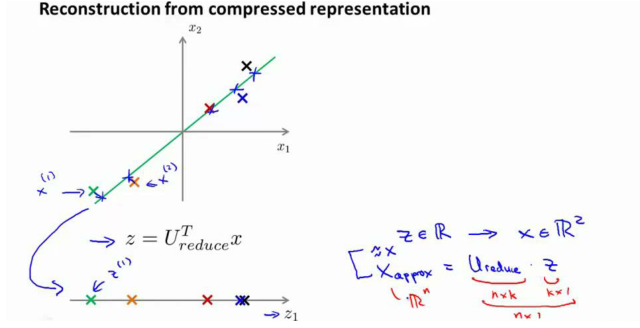
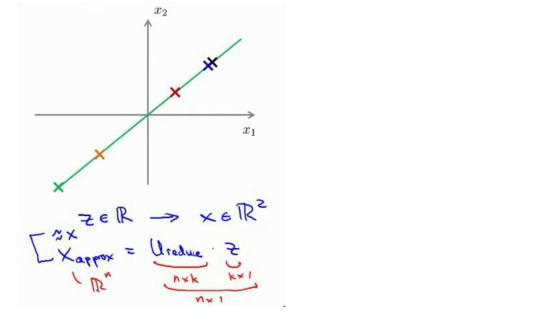
?PCA 作為壓縮算法,可能需要把 1000 維的數據壓縮?100 維特征,或具有三維數據壓縮到一二維表示。
所以,如果這是一個壓縮算法,應該能回到這個壓縮表示,回到你原有的高維數據的一種近似。
這是一個漂亮的與原始數據相當相似。所以,這就是從低維表示 Z 回到未壓縮的時表示。
我們得到數據的一個近似的原始數據 X,也把這個過程稱為重建原始數據。
三、 錯誤的應用場景:
錯誤一: 將其用于減少過擬合(減少特征的數量)。這樣做非常不好,不如嘗試歸一化處理。原因在于主要成分分析只是近似地丟棄掉一些特征, 它并不考慮任何與結果變量有關的信息, 因此可能會丟失非常重要的特征。而歸一化處理會考慮到結果變量,不會丟掉重要的數據。?
錯誤二:默認地將主要成分分析作為學習過程中的一部分,這雖然很多時候有效果,最好還是從所有原始特征開始,只在有必要的時候(算法運行太慢或者占用太多內存)才考慮采用主成分分析。
?
?



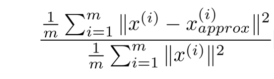

)
 用于數據可視化實驗 -- Matlab版)


)

)










)

