一、前言
視覺系統一共有四個坐標系:像素平面坐標系(u,v)、圖像坐標系(x,y)、相機坐標系(Xc,Yc,Zc)和世界坐標系(Xw,Yw,Zw),如下圖所示。每種坐標系之間均存在聯系,那么如何通過圖像像素坐標定位到世界坐標系的坐標,需要通過相機標定來解決,其中關鍵的算法部分在于坐標系轉換,而變換則需要通過齊次坐標的表示方式來完成。
二、坐標系變換
2.1像素坐標系和圖像坐標系的變換
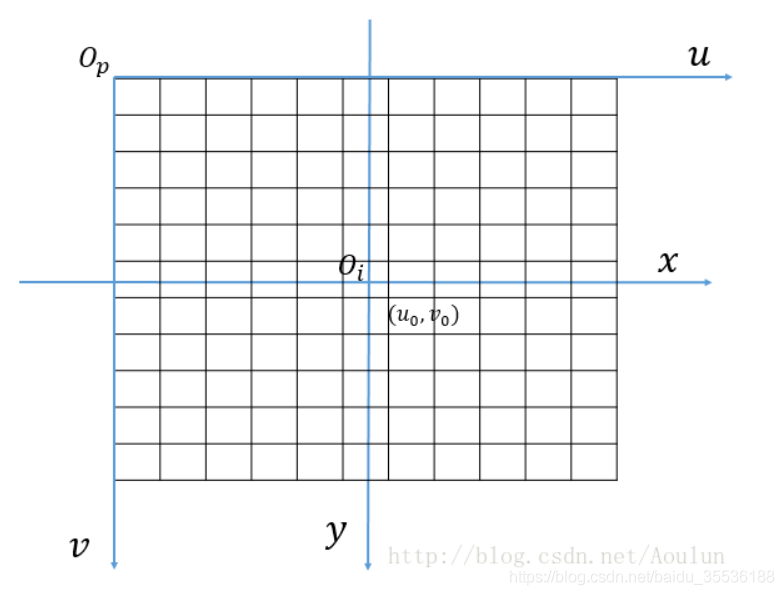
像素坐標就是像素在圖像中的位置。像素坐標系是建立在圖像中的,需要和相機坐標系進行變換,其單位為像素。其的左上角的頂點就是原點(Op),水平向右是u,垂直向下是v軸。
圖像坐標系的單位為毫米,這是因為像素坐標沒辦法反應圖片中點的具體尺寸大小,所以需要圖像坐標系來表示,原點為Oi,為光軸與成像平面的交點。
兩個坐標系都在成像平面上,只是各自的原點和度量單位不一樣。轉換時需要知道兩個參數(dx,dy),分別表示感光芯片上像素的實際大小。
兩者之間變換需要進行單位上的轉換。在圖中,假設圖像中心的像素坐標是(u0,v0),那么,圖像坐標系的坐標(x,y)與像素坐標系的坐標(u,v)之間的關系可以表示為:
u=x/dx+u0u=x/dx+u0u=x/dx+u0
v=y/dy+v0v=y/dy+v0v=y/dy+v0
轉換為齊次坐標:
[uv1]\begin{bmatrix} u\\ v\\1\end{bmatrix}???uv1????=[1/dx0u001/dyv0001]\begin{bmatrix} 1/dx&0&u0\\ 0&1/dy&v0\\0&0&1\end{bmatrix}???1/dx00?01/dy0?u0v01????*[xy1]\begin{bmatrix} x\\ y\\1\end{bmatrix}???xy1????
2.2 相機坐標系與圖像坐標系轉換
相機坐標系是以相機的光軸作為Z軸,光線在相機光學系統的中心位置就是原點Oc(實際上就是透鏡的中心),相機坐標系的水平軸Xc與垂直軸Yc分別于圖像坐標系的X軸和Y軸平行,OcOi之間的距離為f。
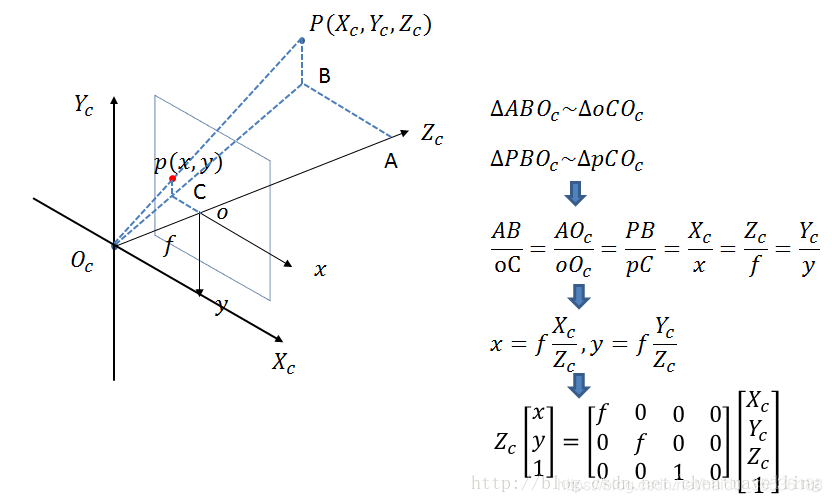 上圖P點為圖像點坐標,B為相機坐標系下物體坐標,可以通過相似三角形求解,如上圖所示,最終也用齊次坐標進行表示。最后的表達式可以看出相機坐標系為三維,圖像坐標系為2維,只能通過齊次坐標變換的形式升維。
上圖P點為圖像點坐標,B為相機坐標系下物體坐標,可以通過相似三角形求解,如上圖所示,最終也用齊次坐標進行表示。最后的表達式可以看出相機坐標系為三維,圖像坐標系為2維,只能通過齊次坐標變換的形式升維。
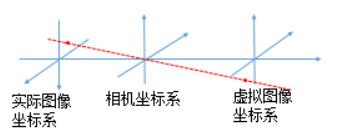
那為什么像素坐標系會在相機坐標系的前面呢?
從原理圖上我們可以看到像平面在鏡面的右面,而在推導相機標定的坐標系關系時,卻認為光線先通過成像平面,再在相機坐標系上匯聚到一個點。其原因是推導的時候,把像平面用虛擬像平面代替了。
2.3世界坐標系與相機坐標系轉換
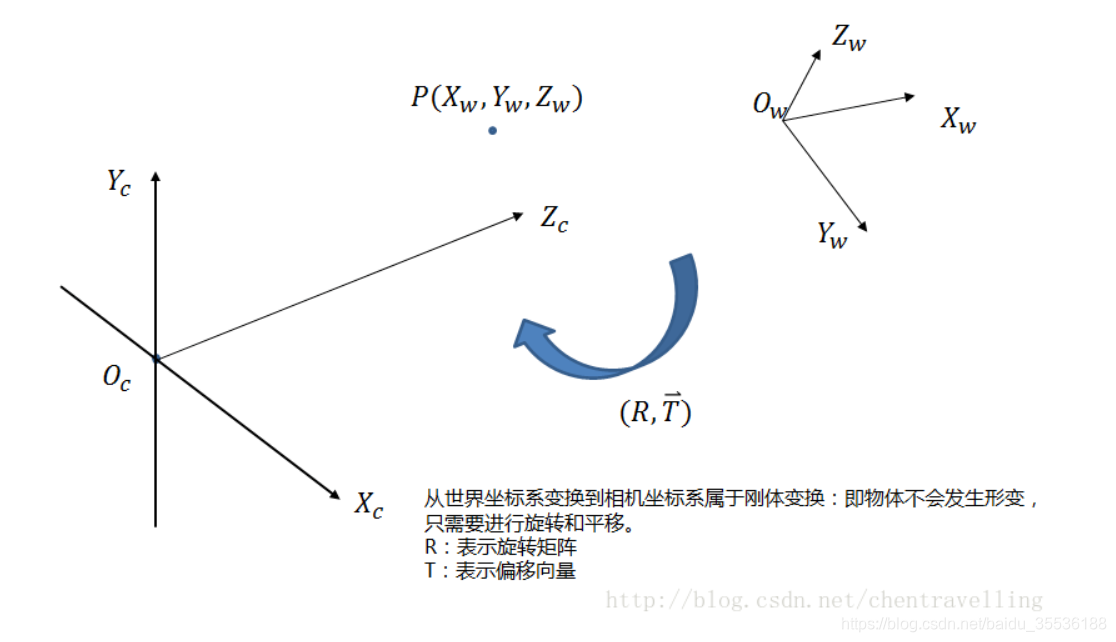
世界坐標系是目標物體位置的參考系,可以根據運算方便與否自由放置,單位為長度單位如mm。從世界坐標系轉換到相機坐標系,涉及到旋轉和平移(其實所有的運動也可以用旋轉矩陣和平移向量來描述)。因為世界坐標系和攝像機坐標都是右手坐標系,所以其不會發生形變(剛性變換)。
計算過程:
平移,相機坐標點(Xc,Yc,Zc)平移距離為(tx,ty,tz)到世界坐標點(Xw,Yw,Zw):
[XwYwZw1]\begin{bmatrix} Xw\\ Yw\\Zw\\1\end{bmatrix}?????XwYwZw1??????=[100tx010ty001tz0001]\begin{bmatrix} 1&0&0&tx\\0&1&0&ty\\0&0&1&tz\\0&0&0&1\end{bmatrix}?????1000?0100?0010?txtytz1??????*[XcYcZc1]\begin{bmatrix} Xc\\Yc\\Zc\\1\end{bmatrix}?????XcYcZc1??????
坐標點(Xc,Yc,Zc)在平移的過程中旋轉一定角度到世界坐標點(Xw,Yw,Zw):
首先給定一個基本旋轉矩陣和基本矩陣:
R=[cosθsinθ?sinθ?cosθ]\begin{bmatrix} cosθ&sinθ\\ -sinθ&-cosθ\end{bmatrix}[cosθ?sinθ?sinθ?cosθ?]
基本矩陣:
[1000010000100001]\begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}?????1000?0100?0010?0001??????
如果坐標點(Xc,Yc,Zc)繞X,Y,Z軸分別旋轉α,β,γ度,則最終的表達式為(哈哈,實在不想自己推導仿射變換的公式了,直接給最終結果,鏈接可以看下方):
那么和平移變換聯合起來可以寫為:

2.4像素坐標系到世界坐標系變換(終極變換)
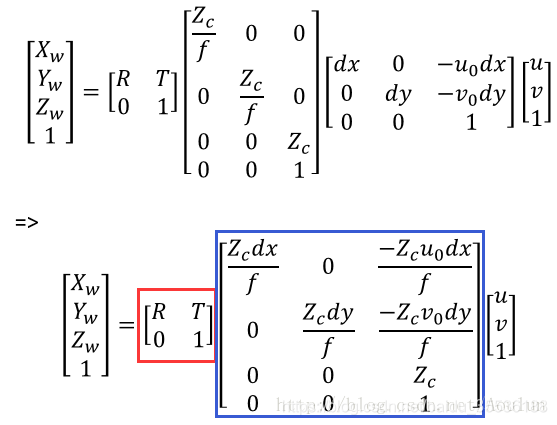
紅框內即為外參,R和T分別為旋轉和平移量。
內參為是相機固有的屬性,實際上就是焦距f,像元尺寸dx,dy。
Zc很明顯,表示的是點離光軸的距離。
參考文章:
相機參數標定(camera calibration)及標定結果如何使用
3d變換基礎:平移、旋轉、縮放(仿射變換)詳解——公式推導
計算機視覺:相機成像原理:世界坐標系、相機坐標系、圖像坐標系、像素坐標系之間的轉換

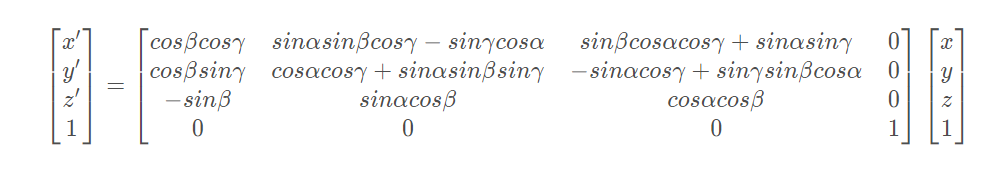
和flatten())

 —— 畸變校正)

)
詳解—— Camera_calibration_multi_image.hdev)


——LeNet卷積神經網絡結構)
主要參數詳述)



—— xyz_attrib_to_object_model_3d)

——AlexNet卷積神經網絡結構)


的使用)
