目錄
一、卷積神經網絡
1、卷積神經的作用
2、LeNet
1)數據庫準備——minst
2)模型·
二、關于卷積神經網絡結構的一些術語定義
1、特征圖(Feature map)
2、height(長度)、width(寬度)、Channel(通道)
3、卷積核(convolution kernel、filter)
4、步長(stride)
1)步長剛好使得卷積核遍歷圖像
2)步長不能使得卷積核遍歷圖像
問題1:原始圖像有一些數據沒有被卷積核訓練怎么解決?
5、小結——原始圖像大小、卷積核大小、步長核特征圖像大小之間有什么關系
三、LeNet卷積神經網絡結構
1、LeNet卷積神經網絡結構模型
2、LeNet第一層卷積層 convolution
1)LeNet第一層卷積層模型
2) LeNet第一層卷積層待求參數個數
3)共享權重(weight sharing)
問題2:上圖的神經網絡和之前學習人工神經網絡(常規神經網絡)有什么區別?
2、LeNet第二層池化層 (subsampling)
問題3:卷積后進行后向傳播時按照正常的BP即可,但是池化后的層進行進行后向傳播到池化前的層呢?
3、LeNet第三層卷積層 (convolution)
4、全連接層(full connection)
1)全連接層的模型和定義
2)全連接層的待定參數
5、輸出層(OUTPUT)
1)目標函數E
問題4:什么是SoftMax?
6、LeNet卷積神經網絡結構參數計算
四、TENSORFLOW實現LeNet-5
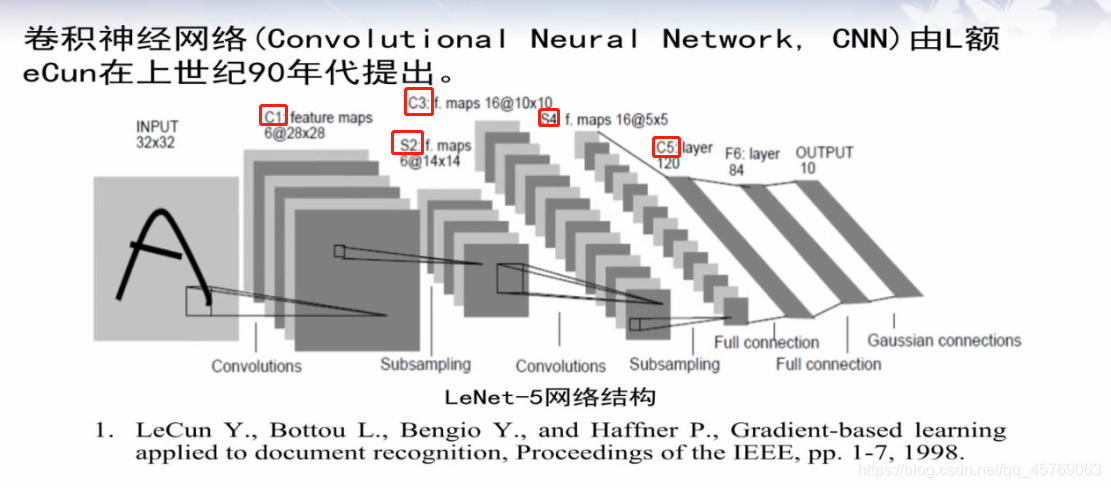
圖 LeNet卷積神經網絡結構前接:《機器學習——深度學習之數據庫和自編碼器》
一、卷積神經網絡
1、卷積神經的作用
由手工設計卷積核轉換為自動學習卷積核
卷積公式有很多:如傅里葉變換、小波變換等
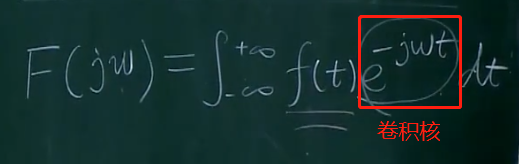
卷積核主要的作用就是將元素先乘再加(積分的本質就是加)
2、LeNet
1)數據庫準備——minst

2)模型·
二、關于卷積神經網絡結構的一些術語定義
1、特征圖(Feature map)
原圖像經過卷積核作用得到的圖像稱為特征圖,如圖 LeNet卷積神經網絡結構所示
2、height(長度)、width(寬度)、Channel(通道)
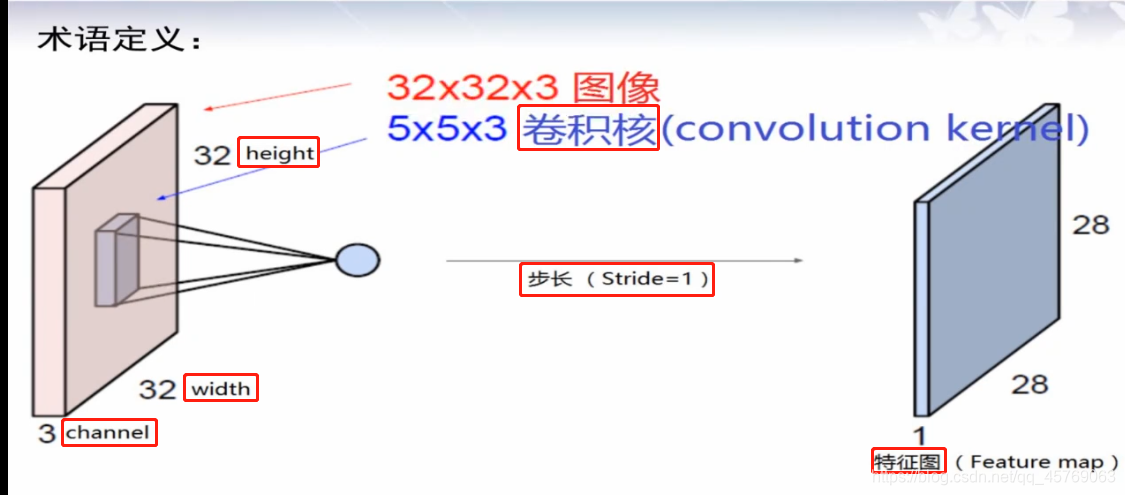
height和width定義了圖像(我們叫做tensor張量)的大小,長寬
channel定義了圖像的顏色,如果是彩色channel=3,表示rgb三原色,如果是黑白二值圖,則channel=1
如圖 LeNet卷積神經網絡結構,圖像的大小為32*32,具體的單位應該是像素,顏色為彩色因為channel=3
3、卷積核(convolution kernel、filter)
如圖 LeNet卷積神經網絡結構,卷積核的大小為5*5,也是彩色,這里的卷積核可以理解為是一個小的圖像,活動范圍是32*32*3的長方體內,按照一定的規律,卷積核可以對圖像進行掃描
以二值圖為例進行說明
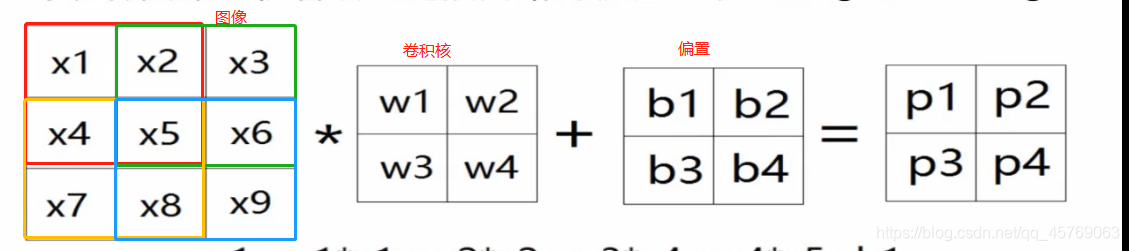
二值圖像大小為3*3*1,卷積核為2*2*1,用卷積核從左上角開始進行掃描,按照一行一行進行,將卷積核與掃描重合的圖像對應的參數進行相乘然后再相加,得到卷積核在該位置的卷積數,如上圖的Pi,上圖還有一個偏置(大家可以按照人工神經網絡的模型去理解這里的b),上圖圖像處每一個顏色框代表卷積核掃描的一個地方,掃描的地方就是在進行卷積,最后會得到如下圖所示的公式。每移動一個地方,就對應得到了特征圖的一個參數
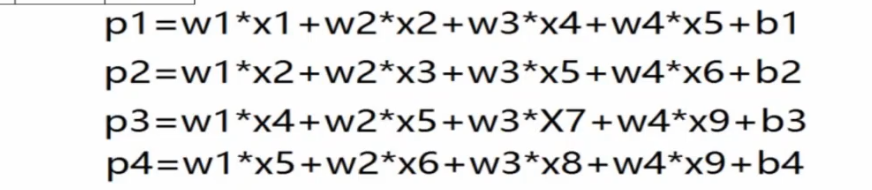
那么卷積核究竟該按照什么規律去移動呢,這就涉及到了步長這個概念。
4、步長(stride)
步長顧名思義就是每一步移動的長度,這里的步長控制的是卷積核掃描的長度,如stride=【1,1】表示的是卷積核每一步向右移動一個單位長度,換行時也是在縱向上移動一個單位長度
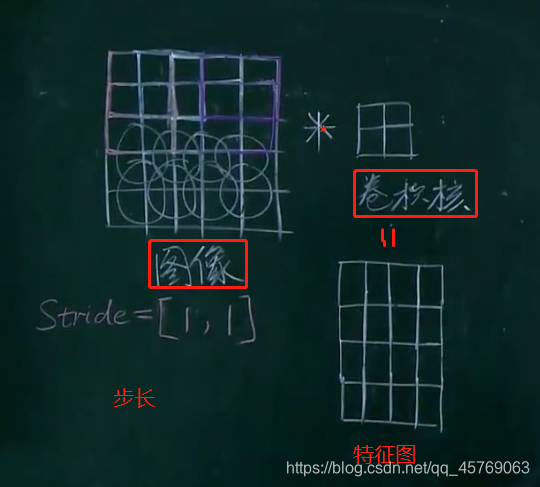
如下圖移動的步長就是【1,1】

1)步長剛好使得卷積核遍歷圖像
圖像5*5*3
卷積核2*2*3
步長【1,1】
特征圖像4*4*1
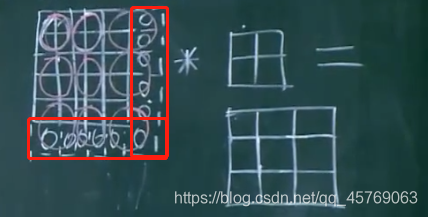
2)步長不能使得卷積核遍歷圖像
圖像5*5*3
卷積核2*2*3
步長【2,2】
特征圖像2*2*1

由上圖可知原始圖像沒有被卷積核全部遍歷(上圖紅色框圖部分)
問題1:原始圖像有一些數據沒有被卷積核訓練怎么解決?
答:補零法(zero-padding)
如下圖所示將原始圖像兩邊用零補齊,使得原始圖像的原有特征能夠全部被卷積核所卷積
最多補零數為四周均不加一層零
5、小結——原始圖像大小、卷積核大小、步長核特征圖像大小之間有什么關系
假設有:
原始圖像大小:M*N*3
卷積核大小:m*n*3
步長:(u,v)
特征圖像大小:K*L*1
則有:
K<=(M-m)/u + 1
L<=(N-n)/v + 1

三、LeNet卷積神經網絡結構
1、LeNet卷積神經網絡結構模型
分為5層
第一層卷積層——convolution
第二層池化層——subsampling
第三層卷積層——convolution
第四層池化層——subsampling
第五層:
全連接層——full connection
全連接層——full connection

2、LeNet第一層卷積層 convolution
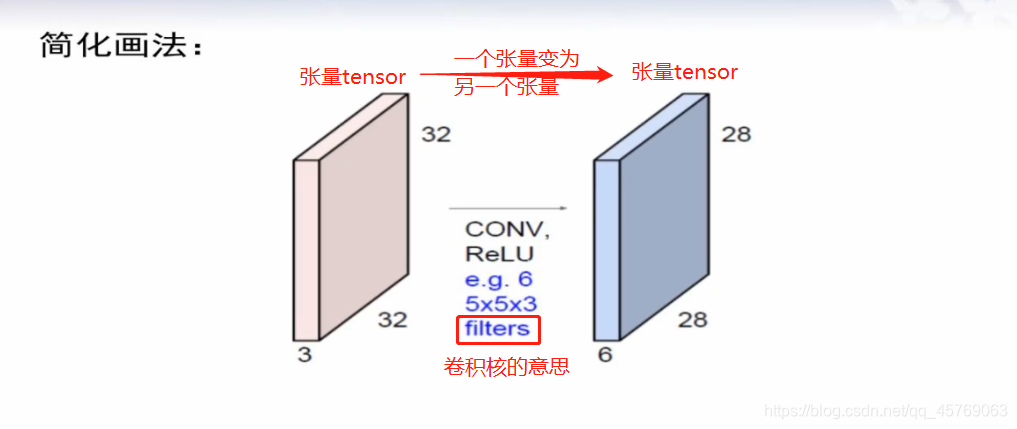
32*32*3——28*28*6
1)LeNet第一層卷積層模型
?
特征圖的個數和卷積核的個數是一樣的,具體點就是特征圖像的channel的值和卷積核的個數相同
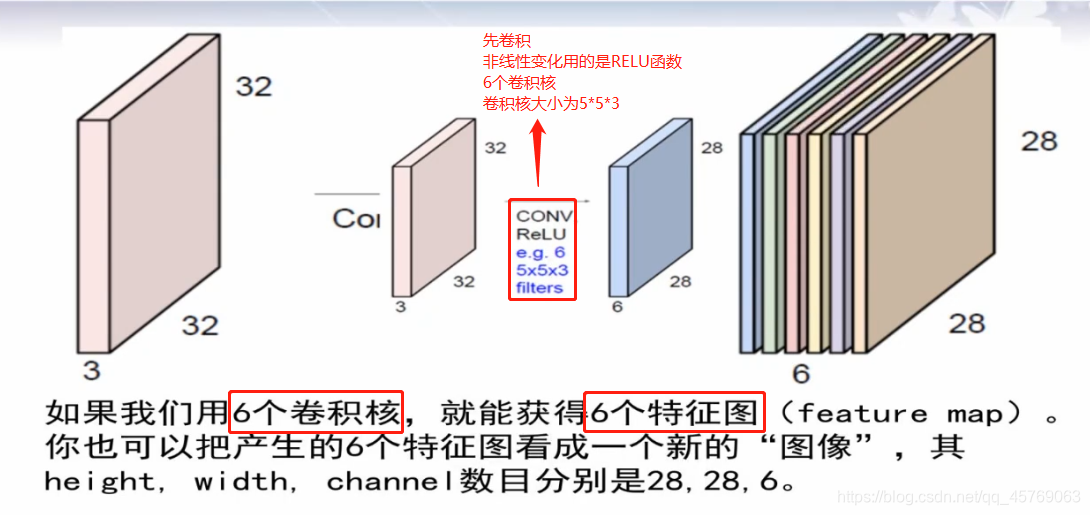
注意:非線性轉換不會改變圖像的大小,只是對圖像的每一個特征進行非線性變化,最后得到的大小和非線性變換前是一樣的
 ?
?
2) LeNet第一層卷積層待求參數個數
首先是一個卷積核中的參數個數為:
m=5*5*3 = 75
在LeNet中有6個卷積核則:6m = 75*6=450
注意:以上的參數的個數沒有偏置,一般一個卷積核是會自帶一個偏置的,即b,所以有卷積核參數為:
6*(m+1)=6*76=456,有沒有偏置有自己定義
實際上b是一個和卷積核大小一樣的矩陣,但是一般將其作為一個參數來進行處理

其實偏置的形式可以通過原始圖像大小、卷積核大小、步長核特征圖像大小之間的關系來進行確定的,先計算出特征圖像的大小(K,L),這樣的話偏置的形式和特征圖像的大小是一樣的
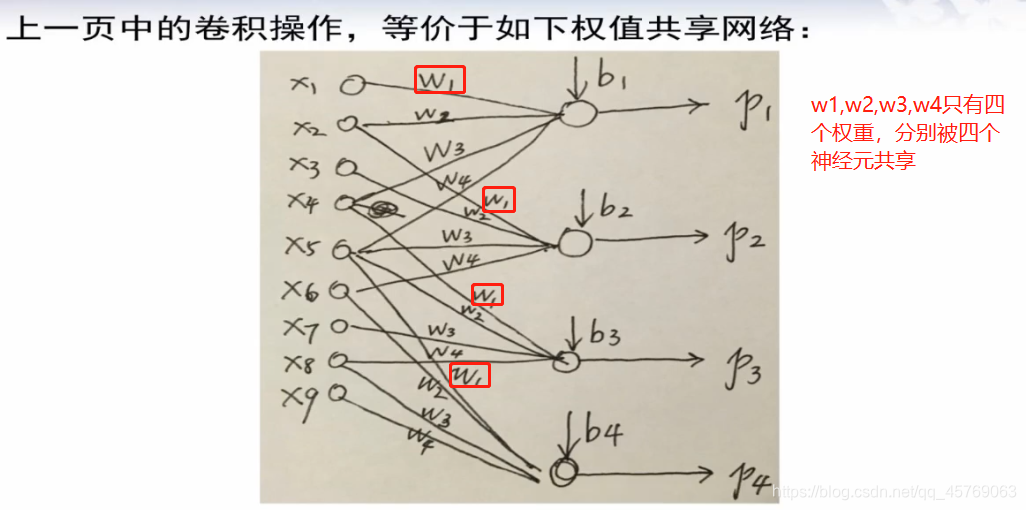
3)共享權重(weight sharing)
共享權重就是同一個權重被不同的神經元之間所共享,或者說不同的神經元之間的權重有相同的
這里可以用類似于神經網絡的方法來表示以下圖的關系

?
問題2:上圖的神經網絡和之前學習人工神經網絡(常規神經網絡)有什么區別?
答:兩個區別:
不本質區別:上圖中,并不是所有的輸入神經元和下一層的神經元都有權重,即只有部分神經元之間進行了連線,而常規的神經網絡是每個神經元之間都有需要連線的即有權重,但是這個區別我們把沒有連線之間神經元的權重看成是0即可,因此此為不本質區別
本質區別:上圖神經網絡的權重是共享的

2、LeNet第二層池化層 (subsampling)
28*28*6——14*14*6
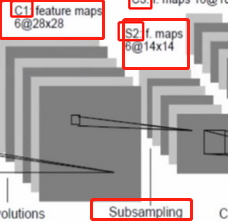
做的事情就是降維采樣,即將第一層得到的特征圖像中的大小分成若干份,將這若干份每一份中的參數特征取一個平均值,作為這一份的新的參數,這個過程叫做池化,最后組合成一個新的特征圖像
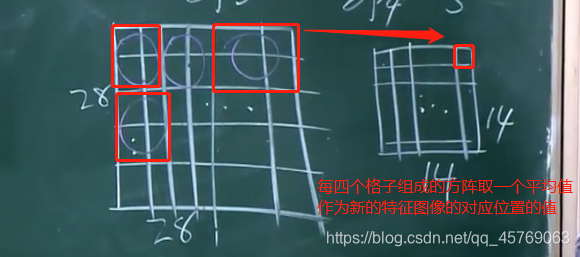
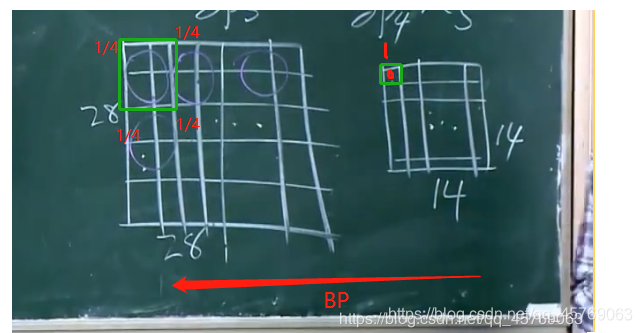
問題3:卷積后進行后向傳播時按照正常的BP即可,但是池化后的層進行進行后向傳播到池化前的層呢?
答:因為池化的過程就是將4個格子取了一個平均值作為池化后的一個格子,那當我們進行后向傳播時,我們將池化后的層的一個格子的1/4梯度作為池化前的4個格子的每一個格子的梯度即可
3、LeNet第三層卷積層 (convolution)
14*14*6——10*10*16
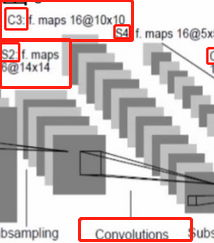

利用和圖像同channel的卷積核去卷積圖像得到的特征圖像的channel=1,這里用了16個和圖像同channel的卷積核去卷積圖像,因此得到的特征圖像的channel=16,至于為什么是10,可以通過《原始圖像大小、卷積核大小、步長核特征圖像大小之間的共關系》來進行求得,(14-5)/1 + 1 = 10
?
4、全連接層(full connection)
這一部分按照人工神經網絡去理解就好了
1)全連接層的模型和定義
在全連接前之前還有一層池化層,這里不再贅述,與第一層的池化層原理一樣
全連接層其實即使常規的神經網絡層了,和卷積層的區別就是:
不本質區別:上圖中,并不是所有的輸入神經元和下一層的神經元都有權重,即只有部分神經元之間進行了連線,而常規的神經網絡是每個神經元之間都有需要連線的即有權重,但是這個區別我們把沒有連線之間神經元的權重看成是0即可,因此此為不本質區別
本質區別:上圖神經網絡的權重是共享的
說簡單一點就是:全連接層的相鄰兩層的神經元是全部都會相互連接的,且權重不會共享,每一對神經元之間的權重是獨立的
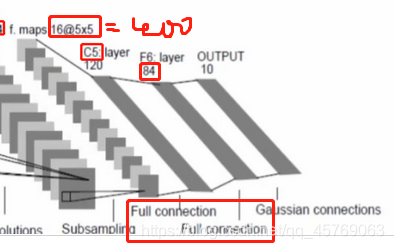
2)全連接層的待定參數
由上圖可知,第一層全連接層的輸入為池化層的輸出,其特征參數為:5*5*16=400,也就是說全連接層的輸入層的神經元個數為400個,輸出層神經元個數為120,則有參數(400+1)*120個,其中加1是因為還有一個偏置;
同理·可得第二層全連接層的輸入層即使第一層全連接層的輸出,有神經元個數120個,輸出層有神經元個數80,則參數的個數為:(120+1)*84
還有最后一層就是全連接層到輸出層(output),易得參數個數為:(84+1)*10

5、輸出層(OUTPUT)
?????? 這一層主要就是將前面通過卷積、池化、全連接得到的預測值輸出,在LeNet卷積神經網絡中,使用的數據庫是Mnist庫,共有10類,因此輸出層為10個神經元。屬于哪一類那么哪一類神經元的輸出值為1,其余9個神經元的輸出為0

這樣就回到我們熟悉的人工神經網絡問題上去了!
具體可見:《【機器學習】神經網絡BP理論與python實例系列》
但是需要注意的是:目標函數發生了改變
1)目標函數E
交叉熵的方式
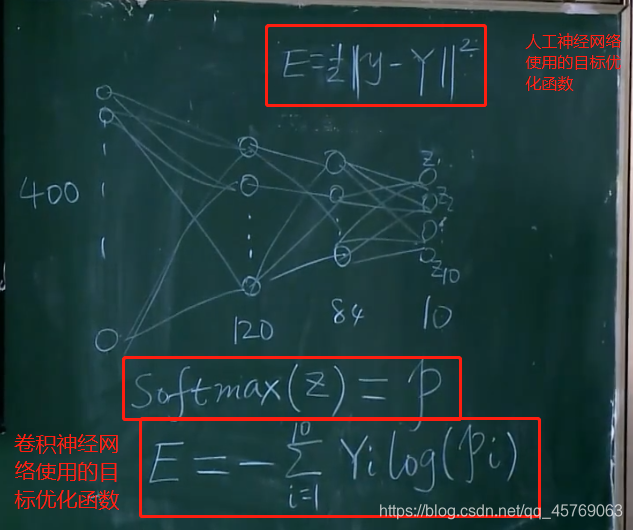
問題4:什么是SoftMax?
答:可見文章:《小白都能看懂的softmax詳解》
6、LeNet卷積神經網絡結構參數計算

注:計算速度取決于卷積層(乘法多)——運行速度,參數個數取決于全連接層——存儲空間
四、TENSORFLOW實現LeNet-5
用戶只需要編寫前向計算就可以,后向傳播是tensorflow包自動計算的,并且tensorflow的數據和神經網絡的描述是分開的,先是對神經網絡進行描述,然后再將數據參數帶入到神經網絡中進行訓練測試等。

 ?
?
 ?
?
主要參數詳述)



—— xyz_attrib_to_object_model_3d)

——AlexNet卷積神經網絡結構)


的使用)


—— calibrate_sheet_of_light_calplate.hdev)






