堆的實現（堆的插入、堆的刪除等）超級全

一、前期基礎知識

1.樹結構

①樹的定義

樹是一種非線性的數據結構，它是由n（n>=0）個有限結點組成一個具有層次關系的集合。把它叫做樹是因為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。

②樹的相關概念

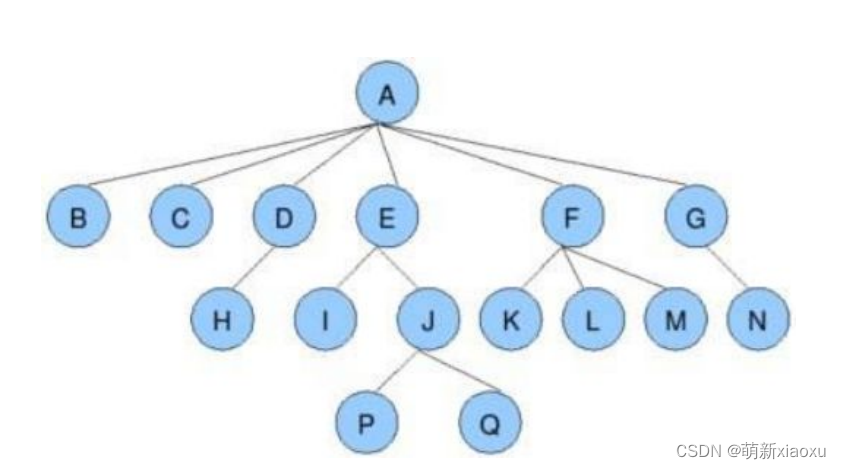
節點的度：一個節點含有的子樹的個數稱為該節點的度； 如上圖：A的為6。
葉節點或終端節點：度為0的節點稱為葉節點； 如上圖：B、C、H、I…等節點為葉節點。
非終端節點或分支節點：度不為0的節點； 如上圖：D、E、F、G…等節點為分支節點。
樹的度：一棵樹中，最大的節點的度稱為樹的度； 如上圖：樹的度為6。
節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推。
樹的高度或深度：樹中節點的最大層次； 如上圖：樹的高度為4。
n個結點的樹，有n-1條邊。

一棵樹有以下三部分組成
根節點，無前驅結點。
葉結點，度為0，又稱終端結點
非終端節點，分支節點，度不為0

一棵樹是由根節點和n顆子樹構成的，子樹一定不能相交，除了根節點外，每一個結點都有且僅有一個父節點。

如果不是樹結構，那就是圖結構。

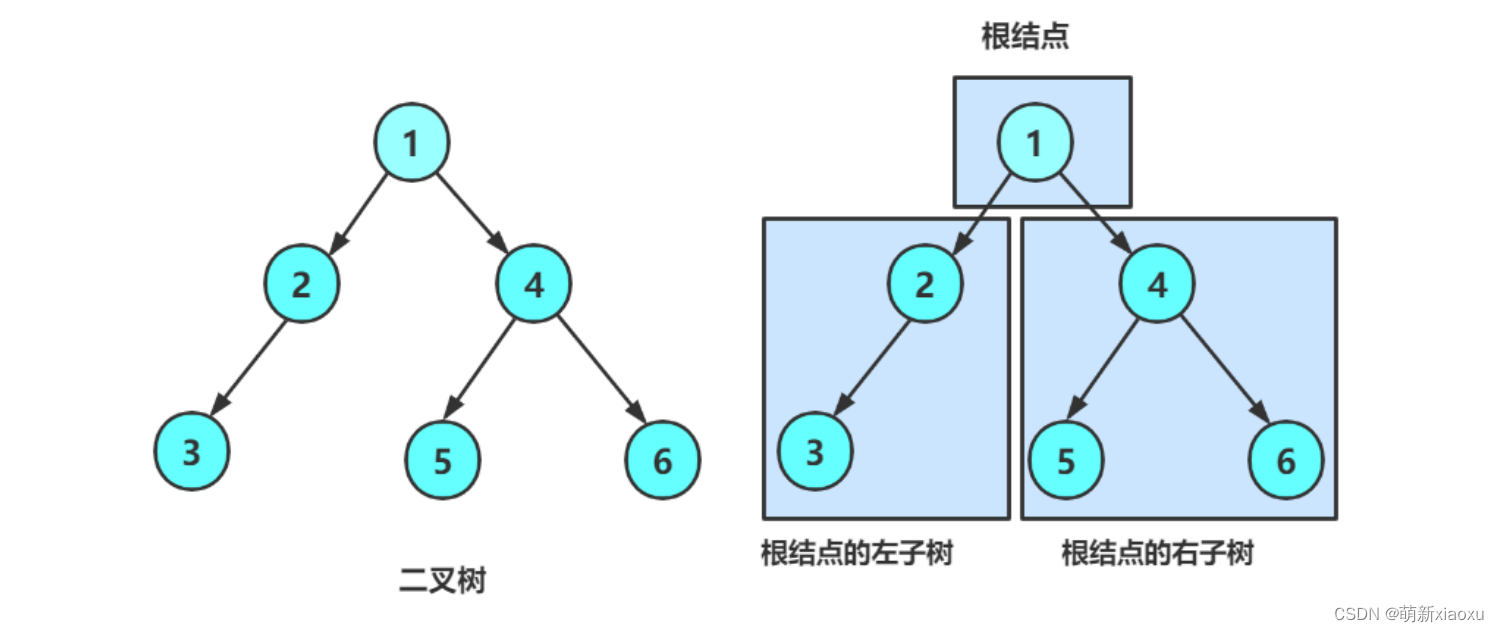
③二叉樹

每一個結點的度不一定都是2，整個二叉樹里不存在度大于2的結點。

1. 或者為空
2. 由一個根節點加上兩棵別稱為左子樹和右子樹的二叉樹組成

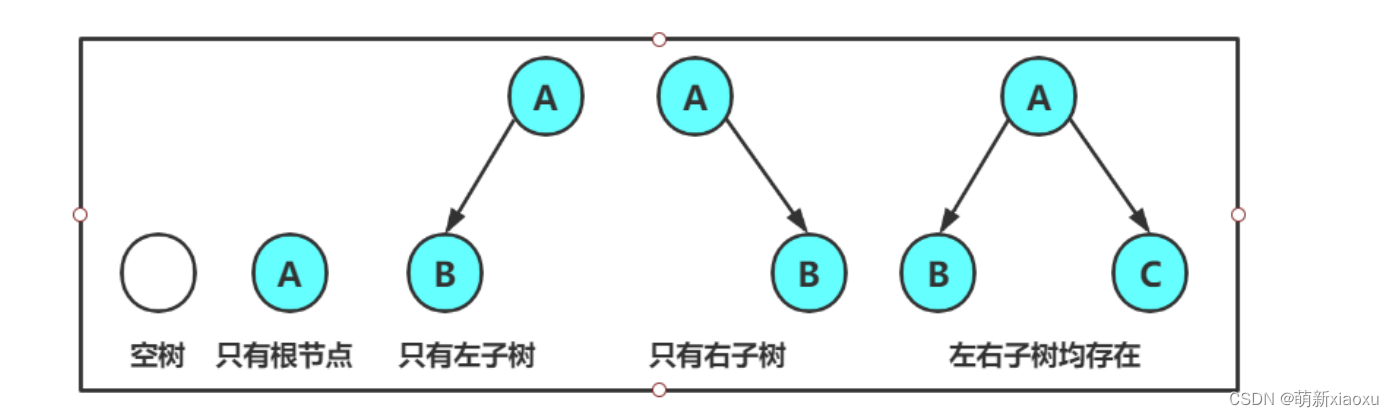
④滿二叉樹和完全二叉樹

a.滿二叉樹

滿二叉樹
一個二叉樹，如果每一個層的結點數都達到最大值，則這個二叉樹就是滿二叉樹。也就是說，如果一個二叉樹的層數為K，且結點總數是2 ^ k - 1 ，則它就是滿二叉樹。

b.完全二叉樹

完全二叉樹
前（n - 1）層是滿的
最后一層不滿，但是從左到右必須連續排布，最少1個，最多2 ^ (n - 1）個。

⑤二叉樹的性質

1. 若規定根節點的層數為1，則一棵非空二叉樹的第i層上最多有2 ^ (i - 1)個結點.
2. 若規定根節點的層數為1，則深度為h的二叉樹的最大結點數是2 ^ h - 1
3. 對任何一棵二叉樹, 如果度為0其葉結點個數為n0 , 度為2的分支結點個數為n2 ,則有n0 ＝ n2 + 1
4. 若規定根節點的層數為1，具有n個結點的滿二叉樹的深度，h= log2底（n + 1）。(ps： 是log以2為底，n+1為對數)
5. 將二叉樹的每一個結點按層次從0到n編號：
   0
   1 2
   3 4 5 6
   7 8 (7，8為3的子節點）
   舉個例子，這就是一個完全二叉樹，0 = （1 - 1) / 2, 0 = (2 - 1) / 2，所以parent = (child - 1) / 2, leftchild = parent * 2 + 1, rightchild = leftchild + 1。
   但是注意，一定要在范圍里。

⑥二叉樹順序結構的存儲和鏈式結構的存儲

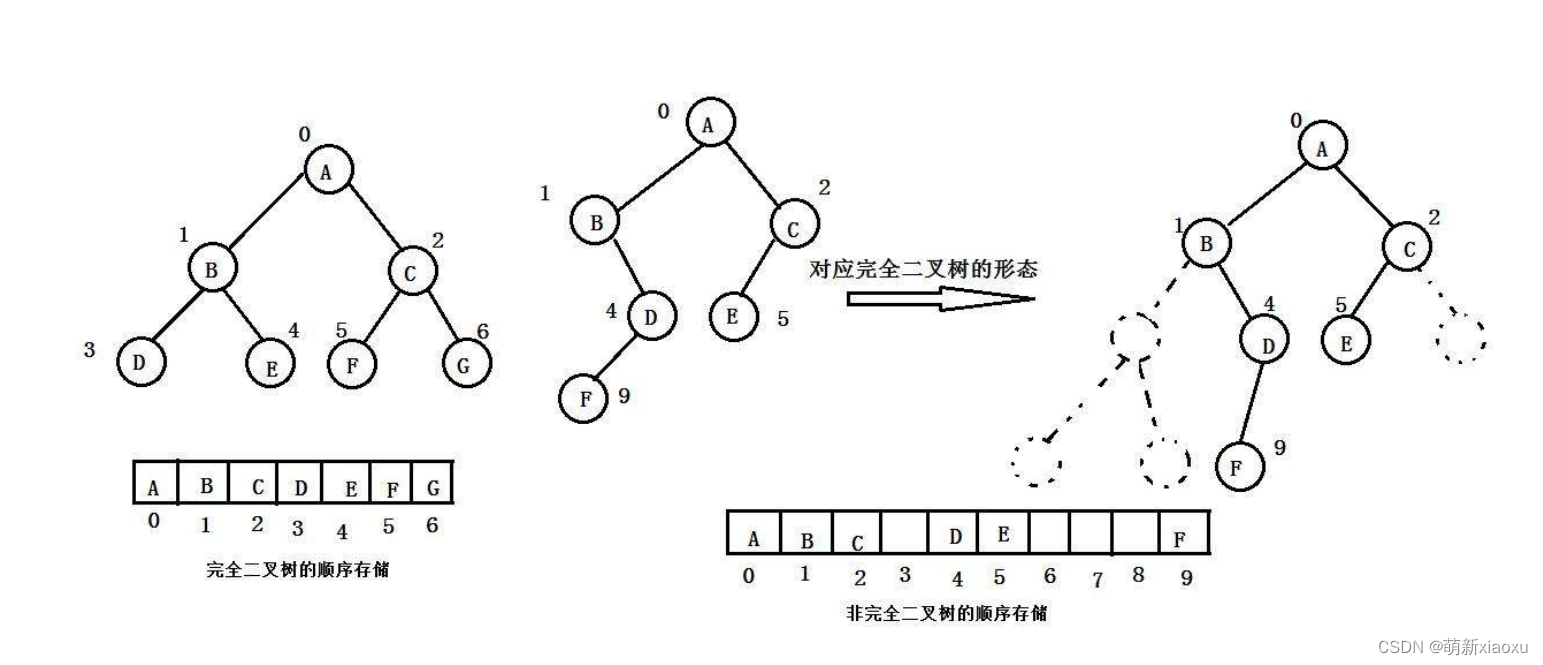
a.順序結構存儲

順序結構存儲就是使用數組來存儲，一般使用數組只適合表示完全二叉樹，因為不是完全二叉樹會有空間的浪費。而現實中使用中只有堆才會使用數組來存儲。二叉樹順序存儲在物理上是一個數組，在邏輯上是一顆二叉樹。

b.鏈式結構存儲

二叉樹的鏈式存儲結構是指，用鏈表來表示一棵二叉樹，即用鏈來指示元素的邏輯關系。 通常的方法是鏈表中每個結點由三個域組成，數據域和左右指針域，左右指針分別用來給出該結點左孩子和右孩子所在的鏈結點的存儲地址 。鏈式結構又分為二叉鏈和三叉鏈，二叉鏈就是兩個指針+數據域，三叉鏈就是兩個指針+指向父節點+數據域，我們暫時先不做重點講解，后續筆者會進行講解。

2.堆結構

1.一段連續的數組數據看作完全二叉樹
2.必須是小堆或者大堆
小堆：任意一個父節點小于等于子節點
大堆：任意一個父節點大于等于子節點

typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;

大家不妨再思考一下，數據結構的目的到底是什么，就是為了方便我們在內存中管理數據，再加上一些可以實現對這段數據進行操作的接口函數來實現我們的目的。

二、堆結構/二叉樹順序結構存儲的實現

1.堆的初始化

void HPIni(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}

2.堆的銷毀

void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0;
}

3.堆的插入

void Swap(HPDataType* p1, HPDataType* p2)
{assert(p1 && p2);HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void HPAdjustUp(HPDataType* p, int child)
{assert(p);int parent = (child - 1) / 2;while (child > 0){if (p[child] < p[parent]){Swap(( & p[child]), ( & p[parent]));child = parent;parent = (parent - 1) / 2;}else{break;}}
}void HPPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : 2 * (php->capacity);HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;HPAdjustUp(php->a, (php->size - 1));
}

當你插入一個新的數據到堆里后，一定要記得你的結構實際是一個二叉樹，而且以小堆為例，如果你插入的數據，比這個結點的父節點小，那就需要向上調整。

4.堆的刪除

void HPAdjustDown(HP* p, int parent)
{assert(p);int child = parent * 2 + 1;//使用假設法while (child < (p->size)){if ((child + 1 < p->size) && (p->a[child + 1] < p->a[child]))//這個真的很重要，值得反復思考，進行交換{child = child + 1;}if (p->a[child] < p->a[parent]){Swap(&(p->a[child]), &(p->a[parent]));parent = child;child = child * 2 + 1;}else{break;}}
}void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&(php->a[0]), &(php->a[(php->size) - 1]));php->size--;HPAdjustDown(php, 0);
}

相信大家一定會有一些問題，因為堆的刪除，是刪除堆頂元素，大家可能會疑問，為什么不能直接頭刪。
原因有以下兩點：
1.順序表時間復雜度是O(N)，過于復雜。
2.如果頭刪之后，整個數組是要向前挪一位的，整棵樹的結構就全部改變了，父子關系，大小關系全部亂了，需要重新改。

所以我們重新選擇一個方法，就是我們將堆頂元素和最后一個元素互換，再尾刪，這樣可以保證兩顆子樹從上到下的整個順序都沒有被改變，向下調整就只需要進入一顆子樹繼續調整就好啦。

5.取堆頂數據

HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);//使用sizereturn php->a[0];
}

6.堆的數據個數

int HPSize(HP* php)
{assert(php);return (php->size);
}

7.堆的判空

bool HPEmpty(HP* php)
{assert(php);/*if (php->size == 0){return true;}else{return false;}*/return (php->size == 0);
}