力扣11. 盛最多水的容器

11. 盛最多水的容器 - 力扣（LeetCode）

難度 中等

給定一個長度為?n?的整數數組?height?。有?n?條垂線，第?i?條線的兩個端點是?(i, 0)?和?(i, height[i])?。

找出其中的兩條線，使得它們與?x?軸共同構成的容器可以容納最多的水。

返回容器可以儲存的最大水量。

說明：你不能傾斜容器。

示例 1：

?

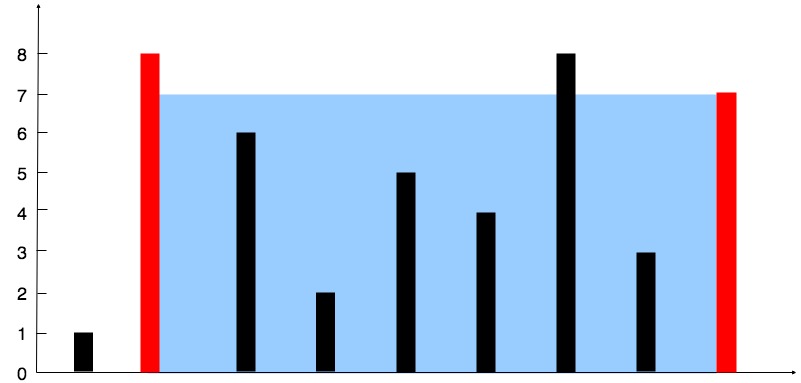
輸入：[1,8,6,2,5,4,8,3,7]
輸出：49 
解釋：圖中垂直線代表輸入數組 [1,8,6,2,5,4,8,3,7]。在此情況下，容器能夠容納水（表示為藍色部分）的最大值為?49。

示例 2：

輸入：height = [1,1]
輸出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 10^4

class Solution {
public:int maxArea(vector<int>& height) {}
};

---

解析代碼

首先想到的是兩層循環的暴力解法，時間復雜度是O（N^2），這里采用雙指針（對撞指針）的思想優化到O（N）：

設兩個指針 left ， right 分別指向容器的左右兩個端點，此時容器的容積 :
v = (right - left) * min( height[right], height[left])?
容器的左邊界為 height[left] ，右邊界為 height[right] 。
為了方便敘述，假設「左邊邊界」小于「右邊邊界」。

• 容器的寬度一定變小。
• 由于左邊界較小，決定了水的高度。如果改變左邊界，新的水面高度不確定，但是一定不會超過右邊的柱子高度，因此容器的容積可能會增大。
• 如果改變右邊界,無論右邊界移動到哪里，新的水面的高度一定不會超過左邊界，也就是不會超過現在的水面高度，但是由于容器的寬度減小，因此容器的容積一定會變小。

由此可見，左邊界和其余邊界的組合情況都可以舍去。所以可以left++跳過這個邊界，繼續去判斷下一個左右邊界。

不斷重復上述過程，每次都可以舍去大量不必要的枚舉過程，直到left與right相遇。期間產生的所有的容積里面的最大值，就是最終答案。

代碼：

class Solution {
public:int maxArea(vector<int>& height) {int left = 0, right = height.size() - 1, ret = 0;while(left < right){int v = (right - left) * min(height[left], height[right]);ret = max(v, ret);if(height[left] < height[right]) // 哪個小哪個就往中間移動{++left;}else{--right;}}return ret;}
};