紅黑樹的概念與性質

?前置知識

在學習紅黑樹之前，最好有二叉查找樹和AVL樹的基礎，因為紅黑樹本質就是一種特殊的二叉查找樹，而紅黑樹的操作中需要用到AVL樹中旋轉的相關知識。至于二叉查找樹和AVL樹，可以參考如下兩篇博客：

二叉查找樹：二叉查找樹-CSDN博客

AVL樹：AVL樹詳解_avl tree-CS? DN博客

---

紅黑樹是一種特殊的二叉查找樹，顧名思義，紅黑樹的一個特性就是每個節點都有一個顏色特征，或為紅或為黑。紅黑樹可以通過一系列的限制規則保證最長路徑小于最短路徑的兩邊，也就是說，紅黑樹的每一條路徑長度的范圍為[N, 2N]，其中N為最短路徑長度。

與AVL樹不同的是，紅黑樹并不是嚴格意義上的平衡二叉樹，降低了插入和旋轉的次數，所以在經常進行增刪的結構中性能比AVL樹更優。

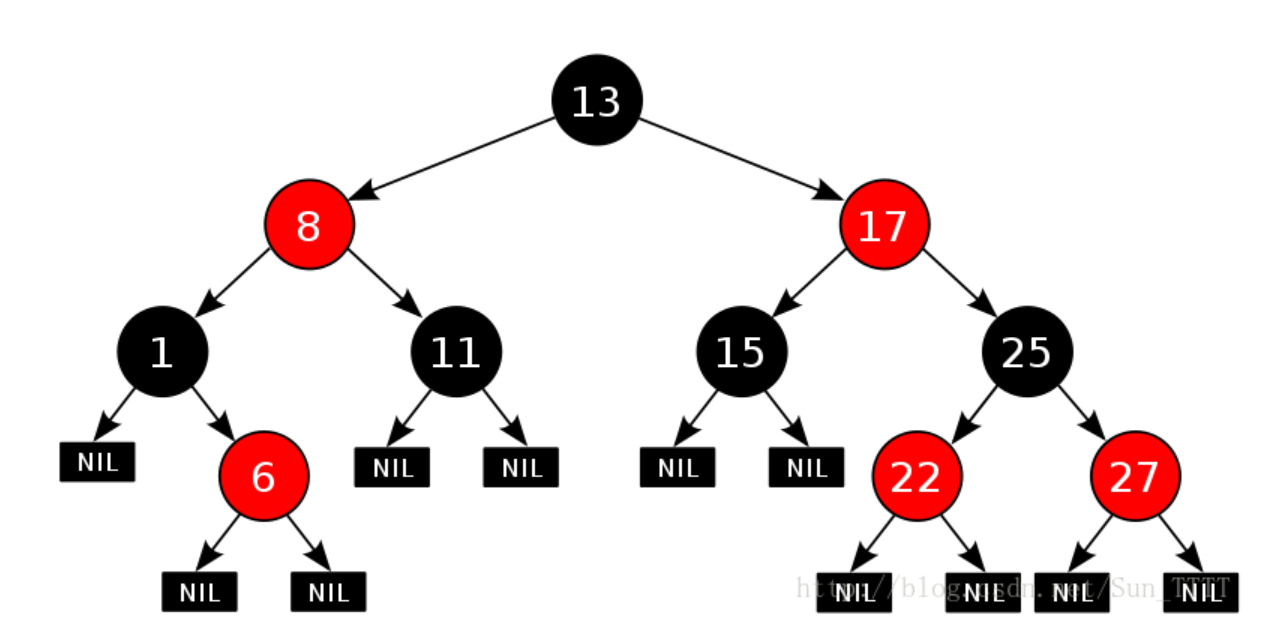
紅黑樹是通過如下5條性質/規則來維護的：

1. 每個結點不是紅色就是黑色
2. 根節點必須是黑色的
3. 紅色節點的孩子結點只能是黑色的，即路徑上不能出現兩個連續的紅節點
4. 從任一節點到其每個葉子的所有路徑，要包含相同數目的黑色節點
5. 所有的葉子結點都是黑結點

注意，由于翻譯的問題，這里的葉子節點實際上指的其實是NIL節點(空節點)。所以，第5條并不算是一條規則，而是一個性質的說明。

那么為什么說這幾條性質就保證了最長路徑不會大于最短路徑的二倍呢？首先，根節點一定是黑的就保證了每條路徑的開始都是一個黑色節點。不能出現連續的紅節點而且每條路徑的黑色結點數量要保持一致，這種的話最短路徑的情況就是整條路徑都為黑色的情況，而最長路徑的情況就是一黑后面緊跟著一紅結點。所以我們很容易應證，最長路徑不會超過最短路徑的二倍。

紅黑樹的插入

紅黑樹本質上就是一種特殊的二叉查找樹，所以大綱上我們依舊是按照二叉查找樹的方式來插入。但是特別的，紅黑樹還維護了結點的顏色這一特性，所以我們還需要額外維護結點的顏色已經遵循上述的條規則/性質。

首先我們要思考，插入新結點時，是將其初始化為紅色還是黑色。我們知道紅黑樹要控制每條路徑的黑色結點相同，所以為了安全起見，一般是插入節點都默認初始化為紅色節點。特別的，紅黑樹還要保證根節點為黑色，所以我們還需要對根節點的情況特殊處理。也就是說，除了根節點的情況外，新插入的結點都是統一初始化為紅色，后續就根據具體情況具體調整了。

那么新插入結點默認為紅結點，就必然會出現插入之后連續兩個紅色結點的情況，那么我們可以將插入之后出現連續紅色結點的各種情況分為兩大類來說：

首先我們規定，cur為當前新插入的節點，p為父節點，g為祖父節點，u為叔叔節點。

• 情況1：cur為紅，p為紅，u存在且為紅，g為黑

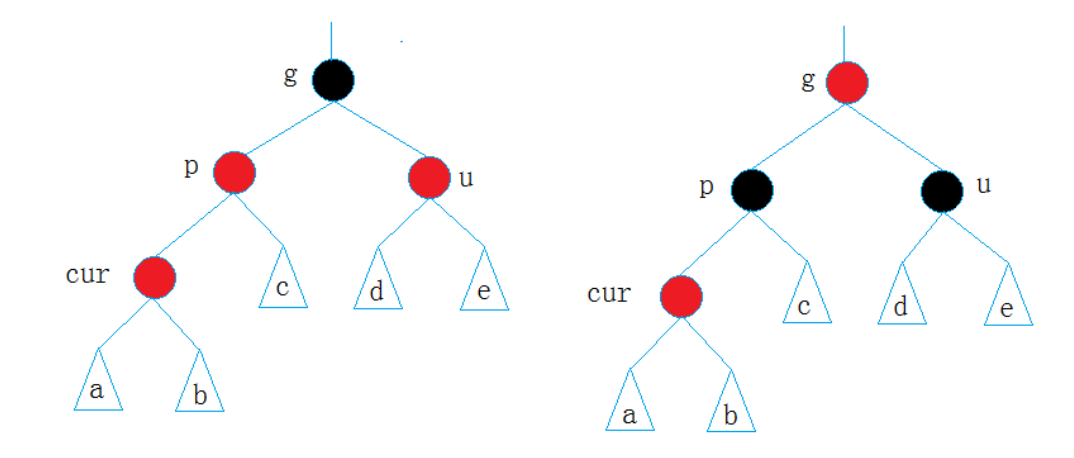
這里需要解釋一下，cur為新插入節點，如果p是紅的，那么根據紅黑樹的性質，g一定是黑的。這種叔叔節點存在且為紅的情況比較好處理，只需要讓父親節點p和叔叔節點u的顏色置黑，g節點置黑即可。

首先，把p和u置黑是因為不能出現連續的紅色節點。而把g置紅是因為g并不一定就是根節點，所以為了不影響本條路徑的黑色節點的數量，是需要將p置紅的。那么如果g真的為根節點的話不就又與性質沖突了嗎？所以我們需要特殊情況特殊處理，一般來說前面照常操作，最后之間暴力將根節點顏色設置為黑色是一種較為簡便好理解的方式。

我們要知道，紅黑樹節點調整要在保證不改變路徑上黑色節點數量的情況下進行調整，所以當叔叔節點存在且為紅的時候，我們就可以通過將叔叔節點置黑，使得在保證路徑上黑色節點數量不變的前提下，調整兩個連續的紅色節點。

• 情況2：cur為紅，p為紅，g為黑，u不存在/u存在且為黑

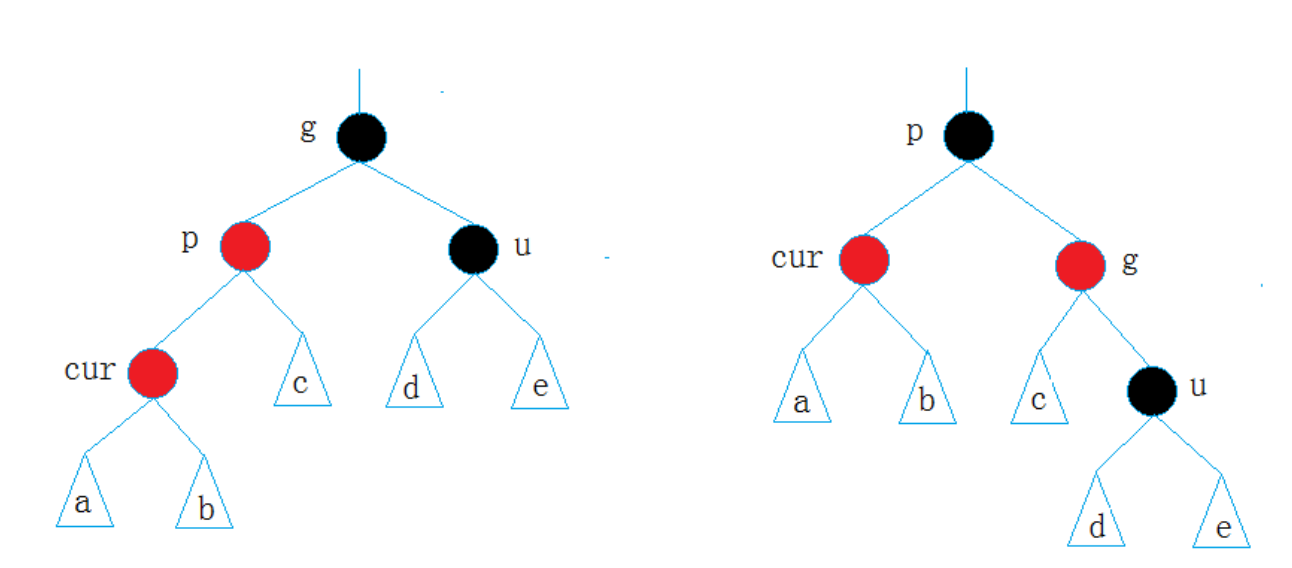
那么當叔叔節點為黑色呢？這時我們就無法直接通過簡單顏色來進行調整了，此時就需要用到AVL樹中提到的4個旋轉了。根據p和cur的位置，共有四種旋轉的情況。不過由于雙旋與單旋之后原來g位置的節點可能為cur也可能為p，所以我們這時就不能單純的將cur置紅或置黑。而是將旋轉之后原g位置的節點置黑，將其兩個子節點置紅，叔叔節點一直是黑的或者空，所以不用對其處理。