1-AI帶你認識TOPSIS

📘 一、TOPSIS 方法簡介

1. ??基本定義：??

??TOPSIS（Technique for Order Preference by Similarity to an Ideal Solution）??，中文通常稱為：

• ?

  ??優劣解距離法??

• ?

  ??逼近理想解排序法??

• ?

  ??理想點法??

它是一種??經典的多指標綜合評價方法??，由 ??C.L. Hwang 和 K. Yoon 于 1981 年提出??，主要用于解決??多方案、多指標的綜合排序與優選問題??。

---

2. ??核心思想：??

??TOPSIS 的核心思想是：通過計算每個評價對象與“理想解”（最優方案）和“負理想解”（最劣方案）之間的距離，來對各個方案進行優劣排序；距離“理想解”越近、距離“負理想解”越遠的方案，其綜合評價結果越好。??

簡單來說就是：

• ?

  先找出所有對象中每個指標的??最好值（正理想解）?? 和 ??最差值（負理想解）??

• ?

  然后計算每個方案到這兩個理想點的??距離??

• ?

  最后根據??接近最優、遠離最劣的程度??進行排序，??距離最優最近、最劣最遠的方案最優??

---

🧩 二、TOPSIS 方法的基本步驟

下面是 TOPSIS 方法的標準操作流程（非常規范、清晰，適合建模與論文使用）：

---

步驟 1：構建原始決策矩陣

假設有 ??m 個評價對象（如方案、城市、企業等）??，??n 個評價指標??，構建初始數據矩陣：

X=?x11?x21??xm1??x12?x22??xm2???????x1n?x2n??xmn???

其中?xij?表示第?i個對象在第?j個指標上的原始取值。

---

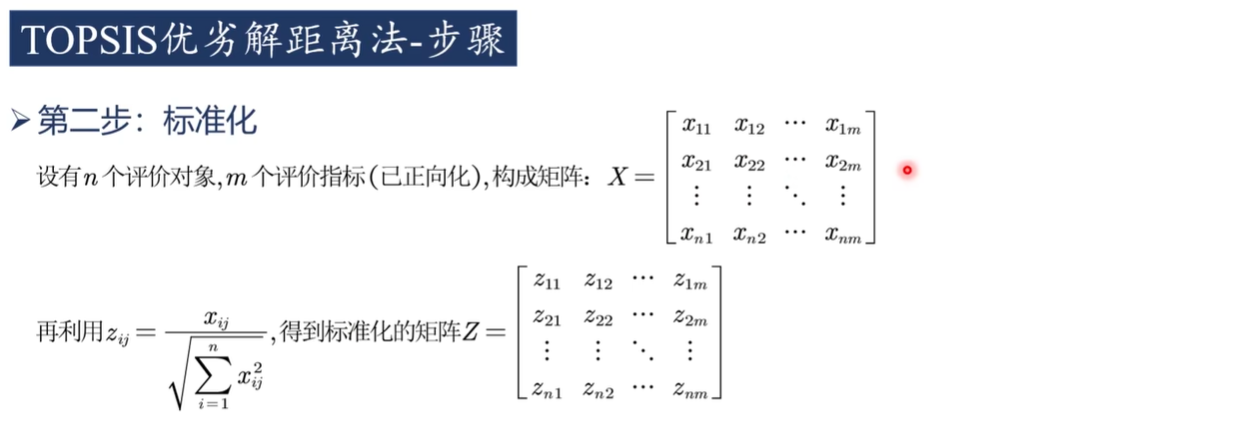
步驟 2：數據標準化處理

由于不同指標可能具有不同的量綱（單位）、數量級，需要對原始數據進行??標準化（歸一化）處理??，消除量綱影響，常用方法為：

（1）向量歸一化（常用）：

yij?=∑i=1m?xij2??xij??

或者（2）極差標準化（區分正向/負向指標）：

• ?

  ??正向指標（越大越好）??：

  yij?=max(xj?)?min(xj?)xij??min(xj?)?

• ?

  ??負向指標（越小越好）??：

  yij?=max(xj?)?min(xj?)max(xj?)?xij??

標準化后得到矩陣?Y=(yij?)m×n?，其中各元素?yij?∈[0,1]

---

步驟 3：確定加權標準化矩陣（可選）

如果各指標的重要性不同，可以引入權重?wj?（如通過 AHP、熵權法等方法獲得），構造??加權標準化決策矩陣??：

V=(vij?)m×n?,vij?=wj??yij?

其中?wj?是第 j 個指標的權重，且滿足?∑j=1n?wj?=1

? 在實際應用中，TOPSIS 往往會結合主觀或客觀權重方法使用，使評價更加科學合理。

---

步驟 4：確定正理想解和負理想解

• ?

  ??正理想解（最優解）???V+：每個指標取??最優值??

  • ?

    對于 ??正向指標??：取最大值

  • ?

    對于 ??負向指標??：取最小值

• ?

  ??負理想解（最劣解）???V?：每個指標取??最劣值??

  • ?

    對于 ??正向指標??：取最小值

  • ?

    對于 ??負向指標??：取最大值

具體為：

vj+?=max(v1j?,v2j?,...,vmj?)或min(v1j?,...,vmj?)（根據指標類型）

vj??=min(v1j?,v2j?,...,vmj?)或max(v1j?,...,vmj?)（根據指標類型）

---

步驟 5：計算各方案到正、負理想解的距離

• ?

  ??到正理想解的距離（歐氏距離）??：

  Di+?=j=1∑n?(vij??vj+?)2?

• ?

  ??到負理想解的距離（歐氏距離）??：

  Di??=j=1∑n?(vij??vj??)2?

其中?Di+?越小越好，Di??越大越好。

---

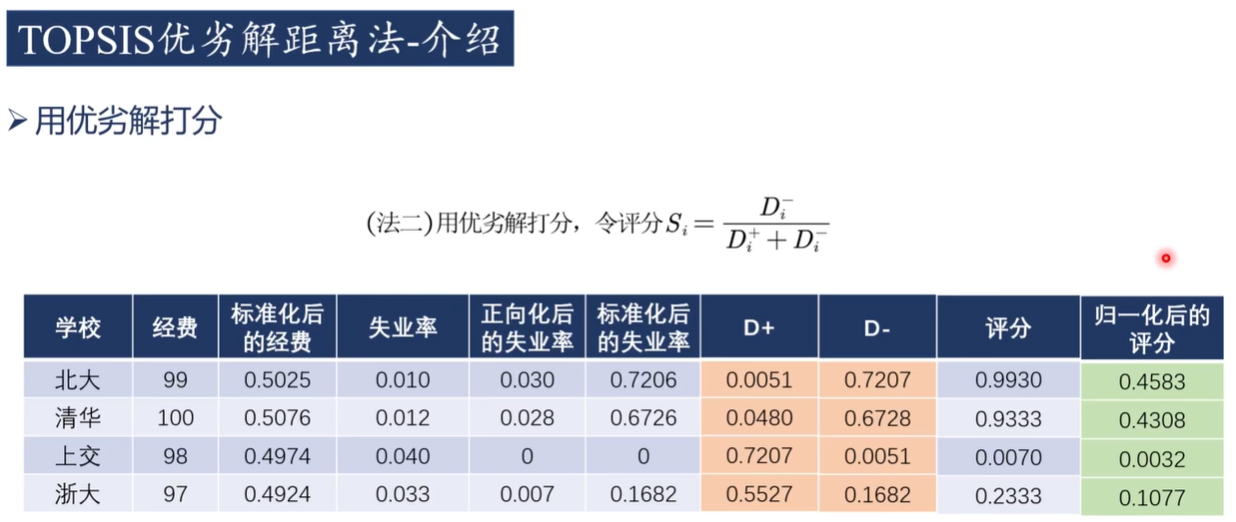
步驟 6：計算相對貼近度（綜合得分）

Ci?=Di+?+Di??Di???,0≤Ci?≤1

• ?

  ??Ci?越接近 1??，說明該方案越接近最優解、遠離最劣解，??評價結果越好??

• ?

  ??Ci?越接近 0??，說明該方案越差

---

步驟 7：排序與決策

• ?

  按照?Ci?值從??大到小??排序

• ?

  ??Ci?最大的方案即為最優方案??

---

? 三、TOPSIS 方法的優點與缺點

? 優點：

1. 1.

   ??直觀易懂??：基于“距離理想解”的思想，邏輯清晰，易于理解與解釋

2. 2.

   ??適用性廣??：適用于多指標、多方案的綜合評價與排序問題

3. 3.

   ??綜合正負兩方面信息??：同時考慮最優和最劣情況，評價更全面

4. 4.

   ??結果明確??：能給出清晰的方案優劣排序，便于決策

5. 5.

   ??可結合權重??：常與 AHP、熵權法等結合，使用主觀或客觀權重，提高科學性

? 缺點：

1. 1.

   ??對數據標準化方法敏感??：不同的標準化方式可能影響結果

2. 2.

   ??依賴權重設置??：權重的合理性直接影響排序結果

3. 3.

   ??僅基于距離度量??：未考慮指標之間的相關性等更復雜信息

---

📚 四、TOPSIS 的應用場景舉例

• ?

  ??方案優選類問題??：如選擇最優投資方案、供應商、旅游地、城市規劃方案等

• ?

  ??績效評價類問題??：如企業績效、政府績效、學校排名、醫院服務評價等

• ?

  ??綜合評價類問題??：如城市競爭力、環境質量、能源效率、技術創新能力等

• ?

  ??多指標決策問題??：幾乎所有涉及多個指標、多個對象優選排序的問題

---

🧠 五、總結一句話：

??TOPSIS（優劣解距離法）是一種基于“距離理想解”思想的多指標綜合評價方法，通過計算各評價對象與最優解和最劣解的距離，得到相對貼近度，從而進行排序與優選，是一種直觀、科學、應用廣泛的決策分析工具。?

2-理論知識

介紹

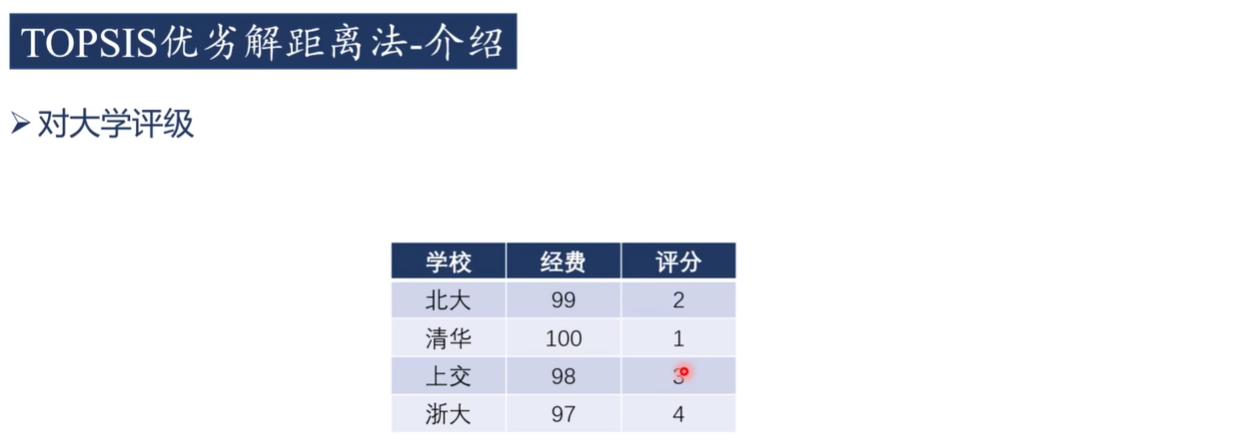
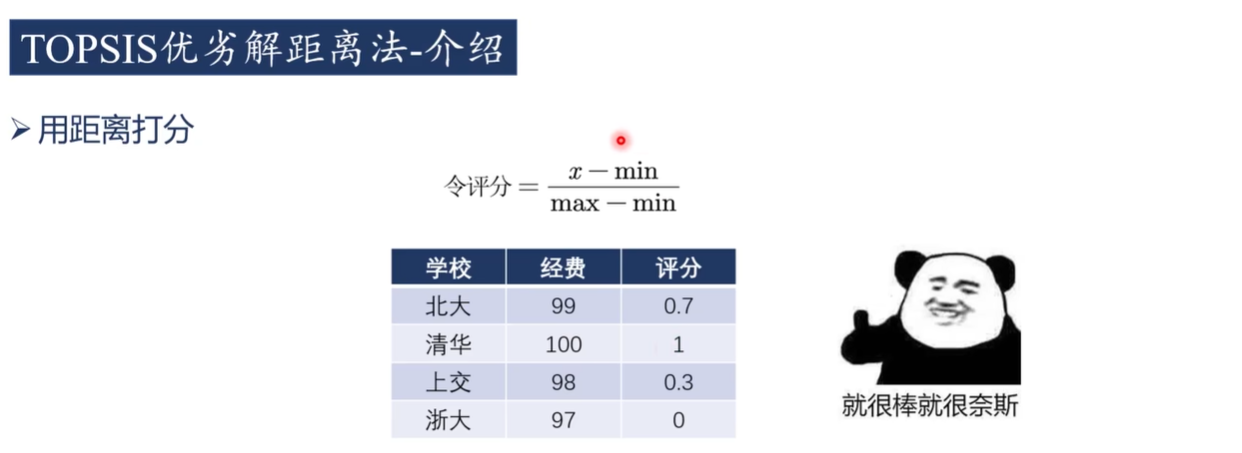
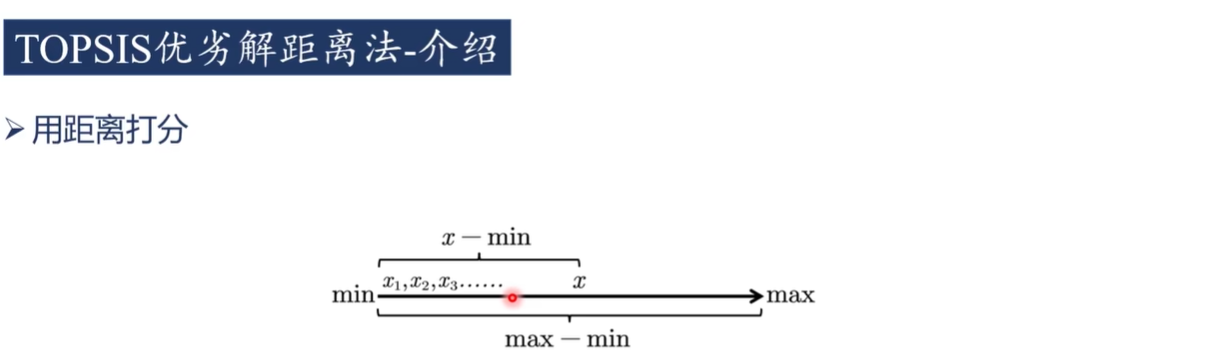
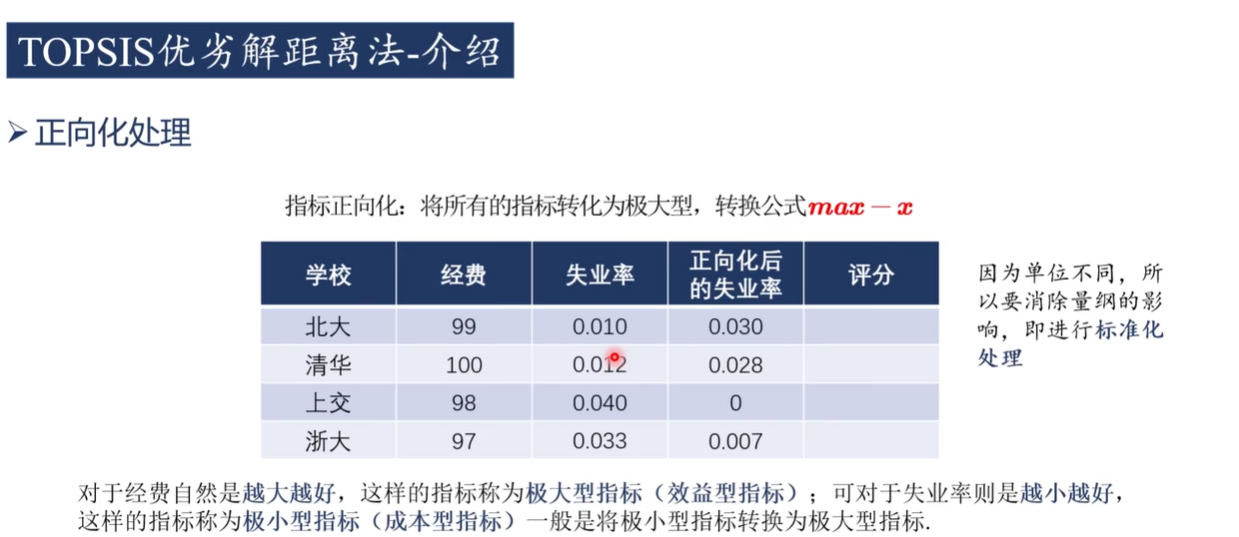
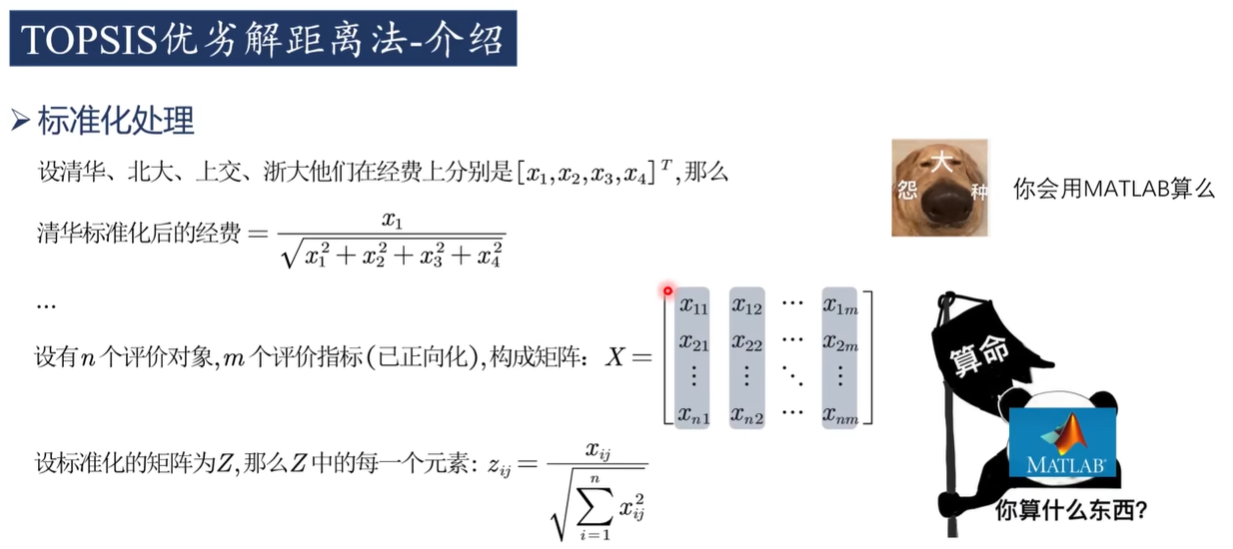
答案：不是

定義

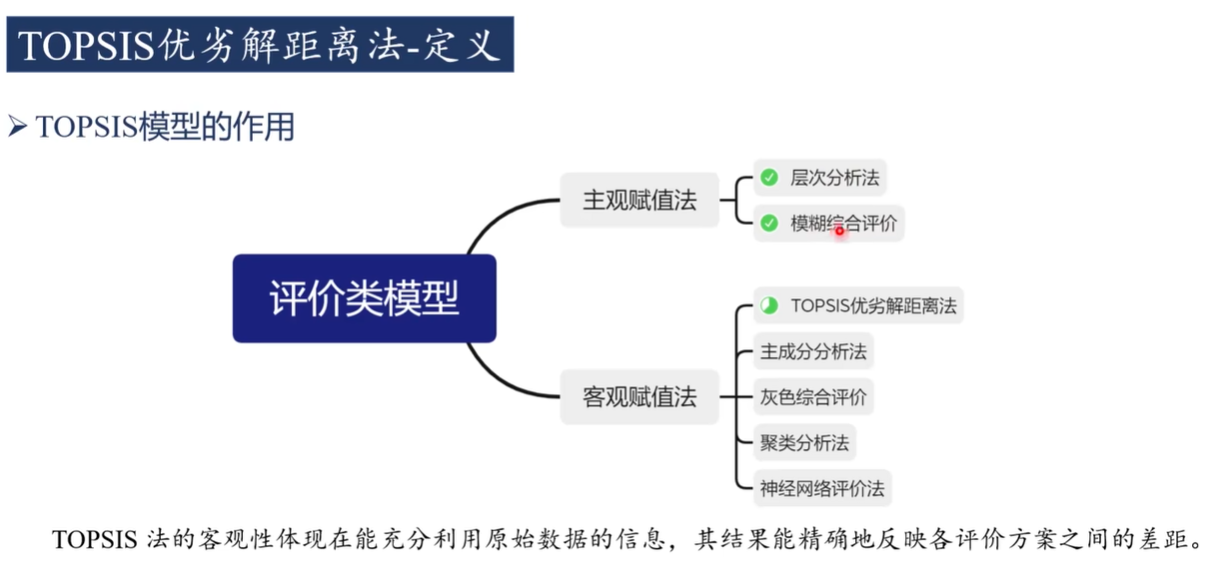
步驟

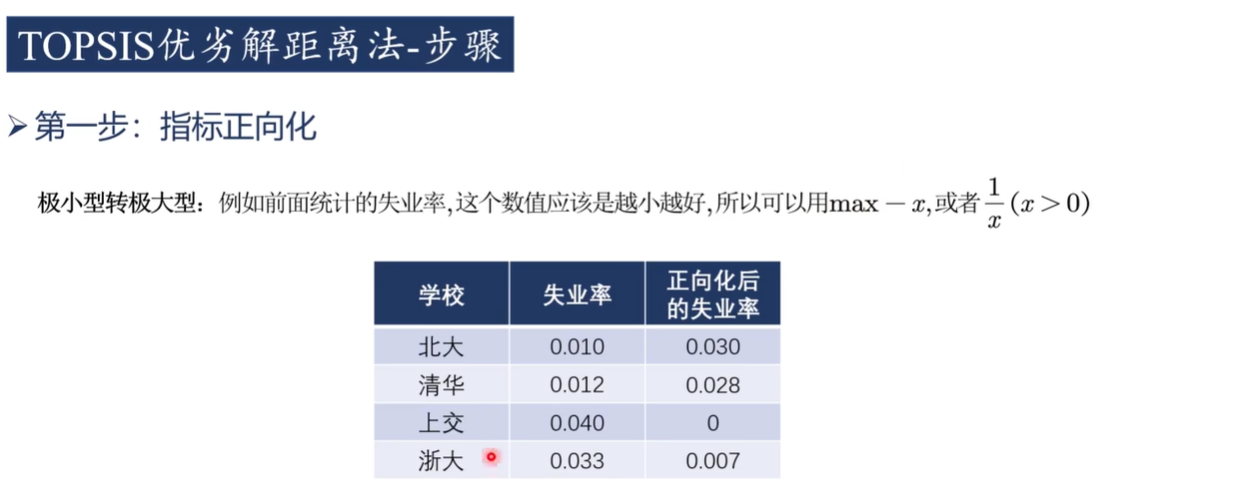
1）正向化

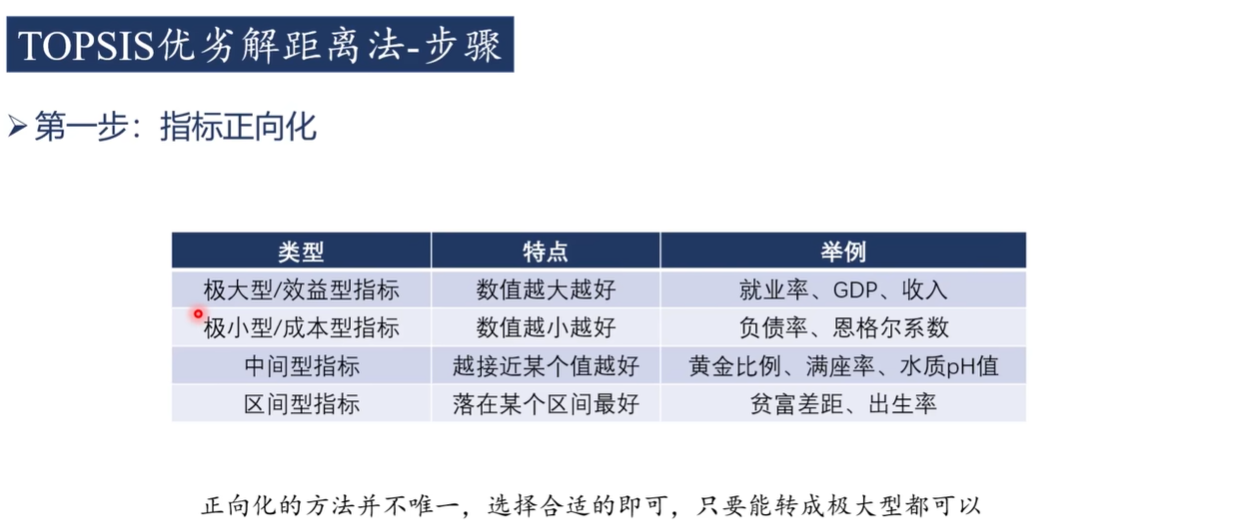
極小型轉極大型

中間型轉極大型

區間型轉極大型

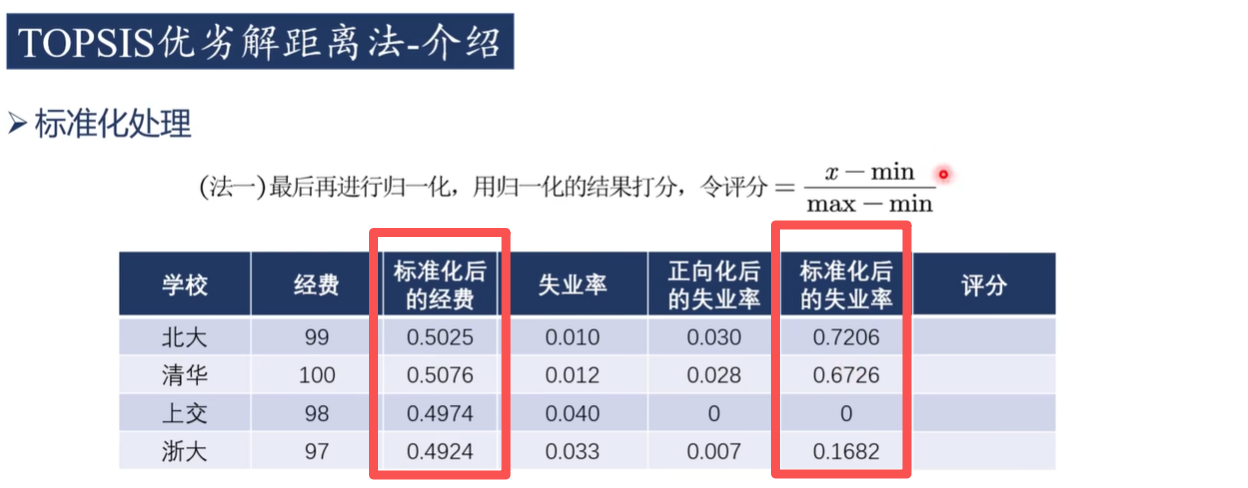
2）標準化

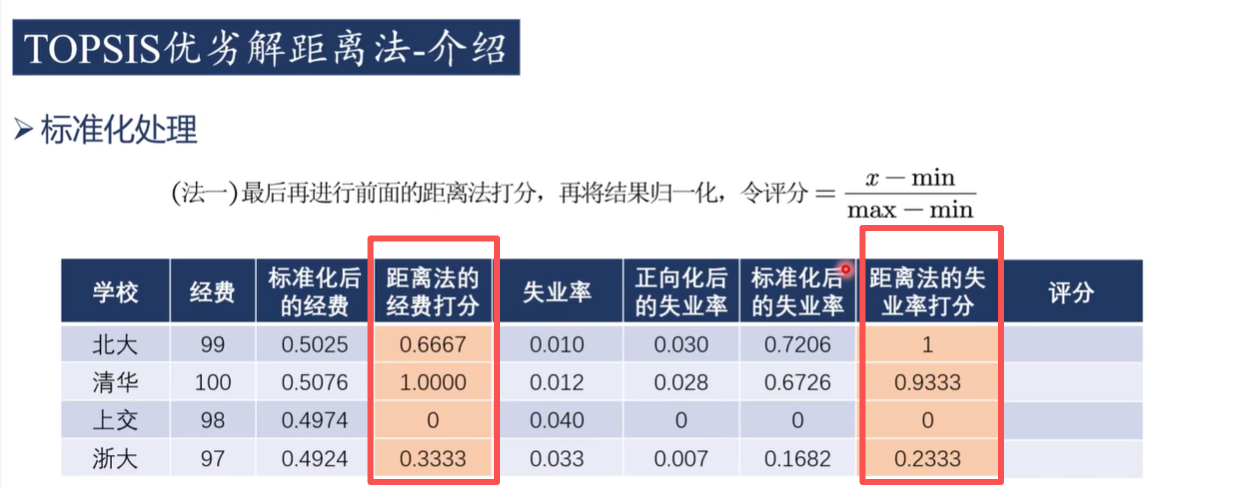
3）優劣解打分

優秀論文

課后習題

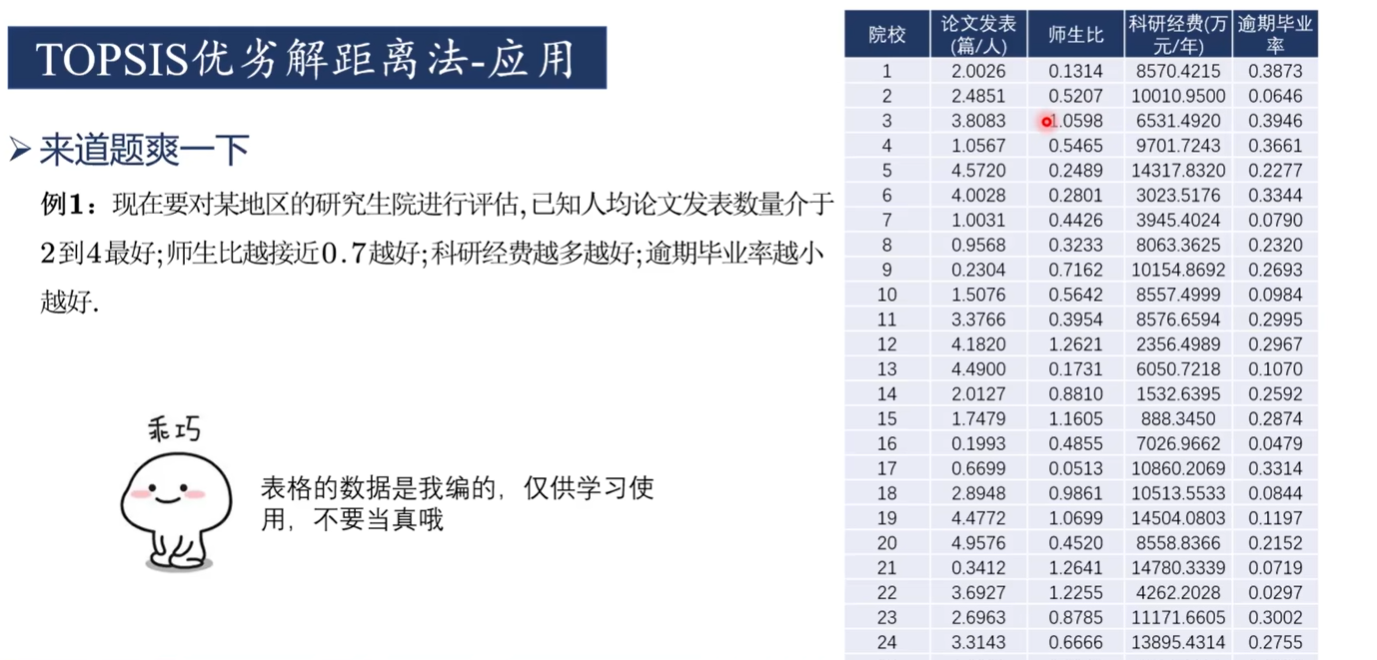
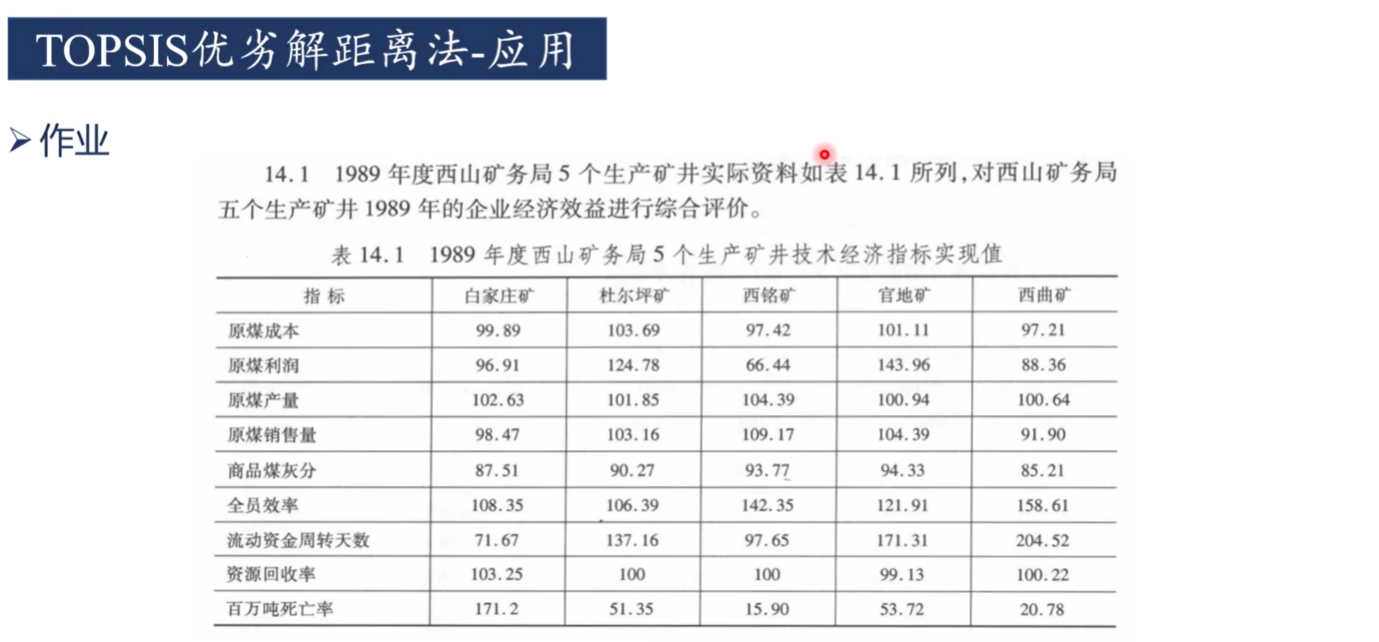
3-基于matlab實現優劣解距離法

源代碼（包含詳細注釋）

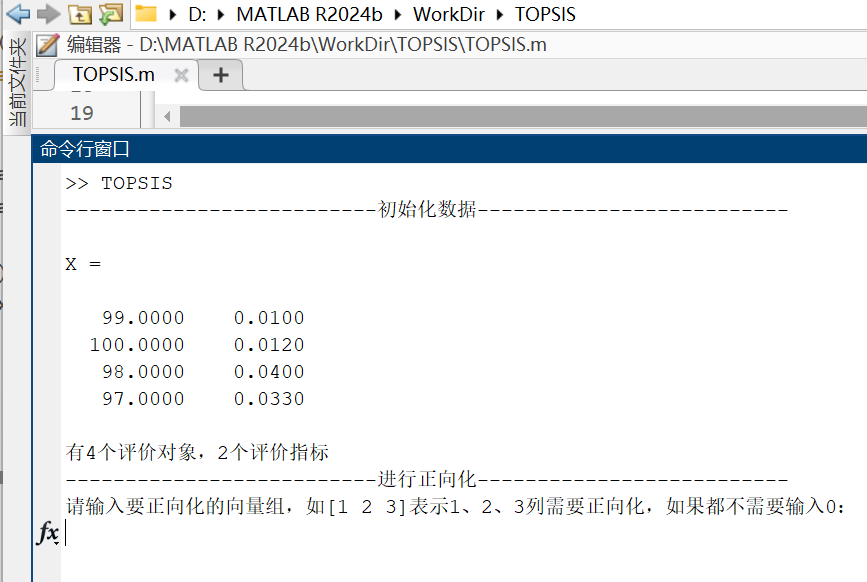
%% 初始化數據
disp('--------------------------初始化數據--------------------------');
X = [99 0.010;100 0.012;98 0.040;97 0.033]
[n,m] = size(X);
disp(['有' num2str(n) '個評價對象，' num2str(m) '個評價指標']);%% 正向化
disp('--------------------------進行正向化--------------------------');
vec = input('請輸入要正向化的向量組，如[1 2 3]表示1、2、3列需要正向化，如果都不需要輸入0：\n')
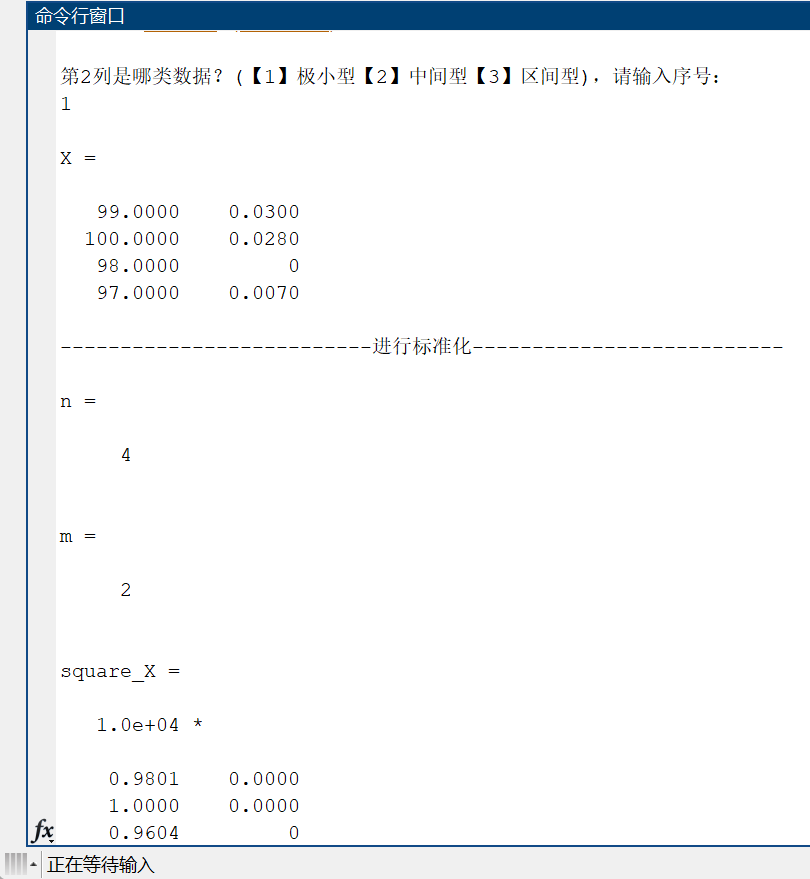
if (vec~=0)% 遍歷需要正向化的列for i = 1:size(vec)option = input(['第' num2str(vec(i)) '列是哪類數據？(【1】極小型【2】中間型【3】區間型)，請輸入序號：\n']);% 極小型if (option == 1)X(:,vec(i)) = Min2Max(X(:,vec(i)))% 中間型elseif (option == 2)best = input('請輸入中間型的最佳值，如180：\n');X(:,vec(i)) = Mid2Max(X(:,vec(i)),best)% 區間型elseif (option == 3)bound = input('請輸入最佳區間，按照"[a b]"的格式，如[80 90]：\n');X(:,vec(i)) = Int2Max(X(:,vec(i)),bound(1),bound(2))elsedisp('輸入的序號錯誤，不存在這類數據\n');endend
end%% 標準化
disp('--------------------------進行標準化--------------------------');
% 行數代表評判對象個數--n
% 列數代表評判指標個數--m
[n,m] = size(X)
exist = 0;
% 遍歷矩陣確認是否存在負數
for i = 1 :nfor j = 1:mif (X(i,j)<0)exist = 1;break;endend
end% 如果不存在負數
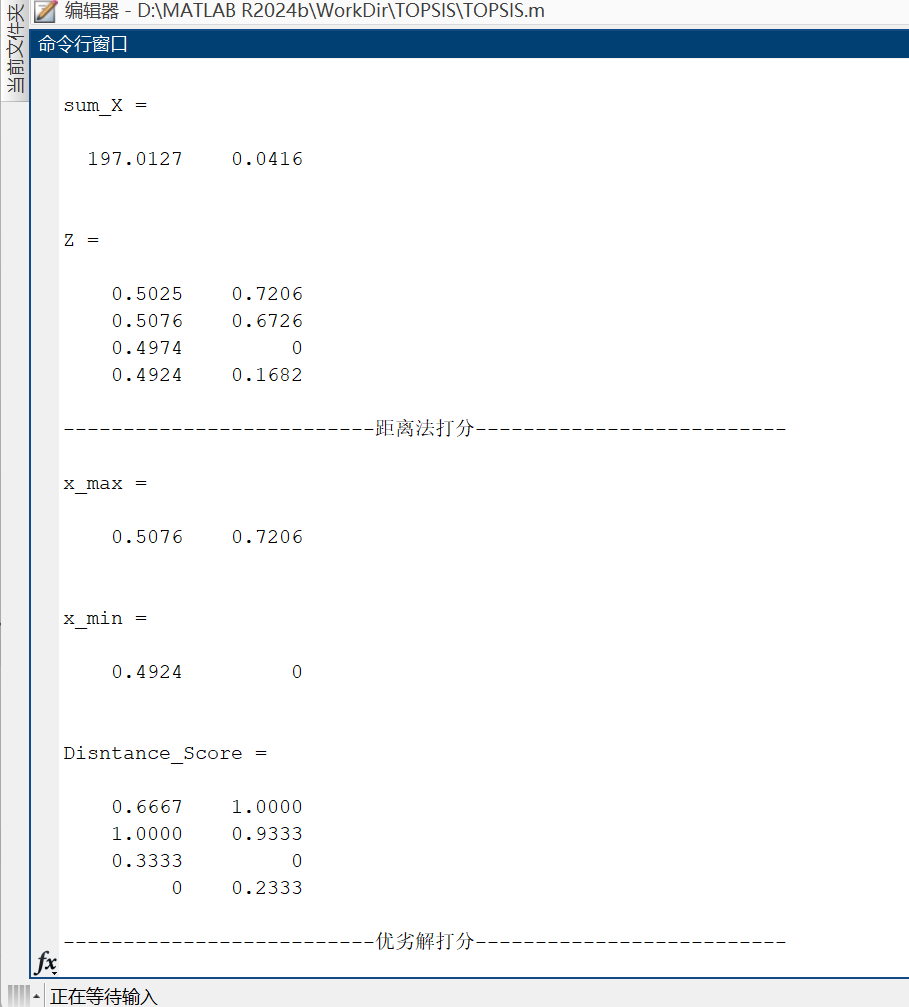
if (exist == 0)% 每個元素都先平方square_X = X.*X% 先按列求和，再開方sum_X = sum(square_X,1) .^ 0.5Z = X ./ repmat(sum_X,n,1)
% 如果存在負數
else% 求出每一列的最大值max_X = max(X,[],1)% 求出每一列的最小值min_X = min(X,[],1)Z = (X - repmat(min_X,n,1)) ./ (repmat(max_X,n,1) - repmat(min_X,n,1))
end%% 方法一：距離法打分
disp('--------------------------距離法打分--------------------------');
% 按照列得到最值元素
x_max = max(Z,[],1)
x_min = min(Z,[],1)
% 距離法打分
Disntance_Score = (Z - repmat(x_min,n,1)) ./ (x_max - x_min)%% 方法二：優劣解打分
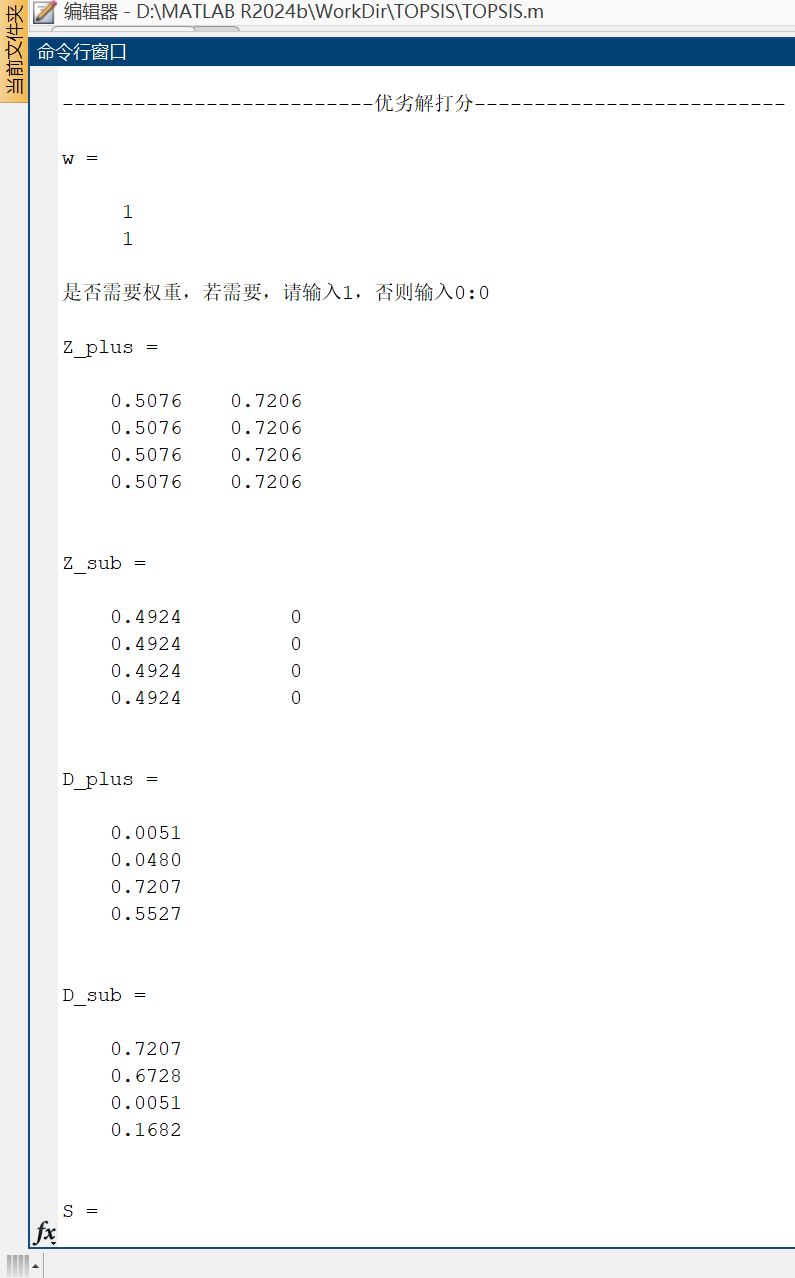
disp('--------------------------優劣解打分--------------------------');
% 生成默認值為1的m維權值列向量
w = ones(m,1)
is_need_weight = input('是否需要權重，若需要，請輸入1，否則輸入0:');
if (is_need_weight==1)w = [];for i = 1 : mw_j = input(['請輸入第' num2str(i) '個指標的權重：']);w = [w;w_j];end
end
% 得到每列最值元素，復制n行變成成n×m型矩陣
Z_plus=repmat(max(Z,[],1),n,1)
Z_sub=repmat(min(Z,[],1),n,1)
D_plus=sum(((Z - Z_plus) .^ 2 ) * w , 2) .^ 0.5
D_sub=sum(((Z - Z_sub) .^ 2 ) * w , 2) .^ 0.5
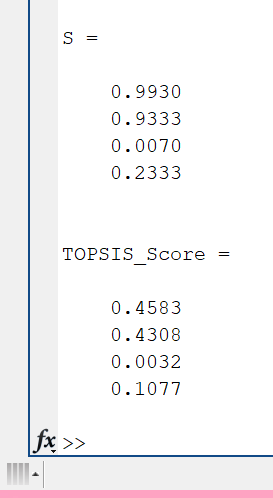
S = D_sub ./ (D_plus+D_sub)
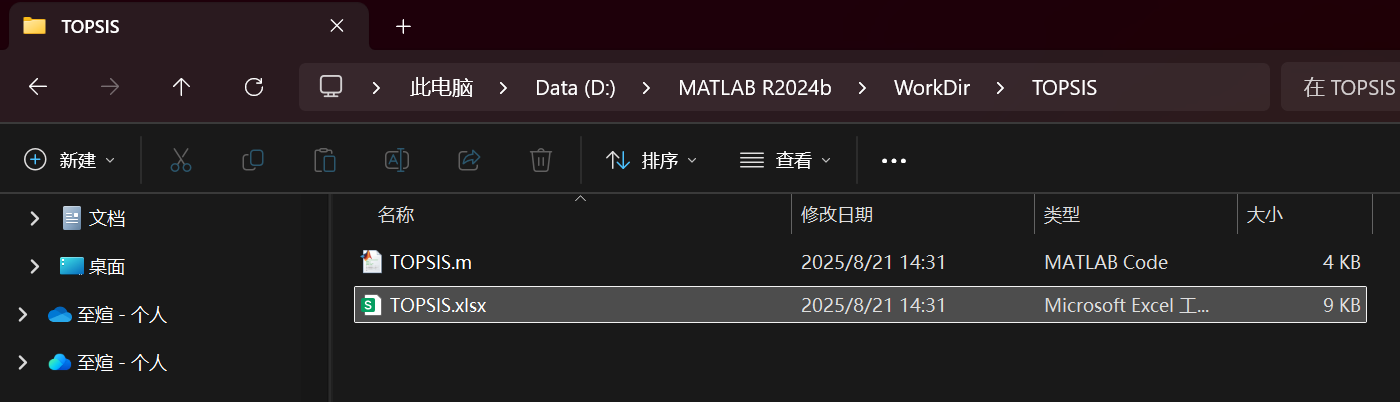
TOPSIS_Score = S ./ sum(S)%% 保存數據到excel表格
xlswrite('TOPSIS.xlsx',TOPSIS_Score);%% 以下是局部函數
% 極小型轉為極大型，傳入參數X為極小型數據，輸出參數res極大型數據
function [res] = Min2Max(X)res = max(X)-X;
end% 中間型轉為極大型，傳入參數X為中間型數據，best為最佳值，輸出參數res為極大型數據
function [res] = Mid2Max(X,best)M = max(abs(X-best));res = 1-abs(X-best)/M;
end% 區間型轉為極大型
% 傳入參數x為區間型數據,a,b分別為區間最佳最小值和最佳最大值
% 輸入參數res為及大型數據
function [res] = Int2Max(X,a,b)M = max(a - min(X),max(X)-b);for i = 1:size(X)if (X(i)<a)X(i) = 1 - (a - X(i))/M;elseif (X(i) >= a && X(i) <= b)X(i) = 1;elseif (X(i) > b)X(i) = 1 - (X(i) - b)/M;endendres = X;
end

運行結果

在同目錄下產生了一個excel文件