目錄

簡介

一、K-means 的核心思想? ?

二、K-means?聚類的工作流程

1. 確定聚類數量 K

2.初始化 K 個簇中心

3.簇分配：將數據點分配到最近的簇

4.更新簇中心：重新計算每個簇的中心

5.判斷是否收斂

6.輸出聚類結果

三、聚類效果評價方式

四、k-means的API

五、案例分析

1.導入必要的庫

2. 數據讀取與特征選擇

3. 尋找最佳 K 值（聚類數量）

4. 可視化不同 K 值的聚類效果

5. 執行最終聚類

6. 評估最終聚類結果

總結

---

簡介

????????我們將聚焦于K-means 聚類算法—— 這一在無監督學習領域應用廣泛且極具實用性的經典算法。無論是在數據挖掘、圖像分割，還是客戶分群等眾多領域，K-means 都以其簡潔高效的特點占據著重要地位。本節課，我們將從算法的基本原理入手，深入淺出地解析 K-means 如何通過迭代優化將數據自動劃分成不同的簇，讓你明白 “物以類聚” 在機器學習中的實現邏輯。我們會詳細講解算法的核心步驟，包括初始質心的選擇、數據點的分配、質心的更新等關鍵環節，同時也會探討算法中 K 值的確定方法以及可能遇到的問題與解決策略。此外，還會結合實際案例，展示 K-means 在真實場景中的應用，幫助你更好地理解和運用這一算法。無論你是機器學習的初學者，還是希望鞏固聚類算法知識的學習者，這一課都能為你帶來清晰的思路和實用的技能。

一、K-means 的核心思想? ?

????????K-means 的目標是將數據集劃分為?K 個簇（clusters），使得每個數據點屬于距離最近的簇中心。通過反復調整簇中心的位置，K-means 不斷優化簇內的緊密度，從而獲得盡量緊湊、彼此分離的簇。

核心概念

• 簇（Cluster）：K-means 通過最小化簇內距離的平方和，實現數據點在簇內的聚集。一個簇是具有相似性的數據點集合，這里的 “相似性” 可根據具體場景定義（如特征值接近、行為模式一致等）。例如，可將電商平臺用戶劃分為 “高頻低消用戶”“低頻高消用戶”“偶爾消費用戶” 等簇。
• 簇中心（Centroid）：作為簇的 “代表點”，其坐標是簇內所有數據點對應特征的平均值，用于衡量簇的中心位置。
• 簇分配與更新：K-means 通過迭代過程優化聚類結果：先隨機確定 K 個初始簇中心，然后將每個數據點分配到距離最近的簇中心所在的簇（完成簇分配）；接著根據新的簇內數據點重新計算各簇的中心（完成簇中心更新）；重復上述步驟，直到簇中心的位置變化小于設定閾值（收斂），最終得到穩定的聚類結果。

二、K-means?聚類的工作流程

1. 確定聚類數量 K

• 首先需要人為指定聚類的數量（即最終要得到的簇的個數），記為?K。
• K 的選擇需要結合業務場景或先驗知識，例如 “將用戶分為 3 類”“將產品分為 5 個等級” 等。若缺乏先驗信息，可通過手肘法、輪廓系數法等輔助確定（后續可延伸補充）。

2.初始化 K 個簇中心

• 從數據集中隨機選擇?K 個數據點，作為初始的簇中心（Centroid）。
• 初始簇中心的選擇會影響最終聚類結果（可能陷入局部最優），因此實際應用中常多次隨機初始化并選擇最優結果，或采用 K-means++ 算法優化初始中心的選擇（使初始中心彼此距離更遠）。

3.簇分配：將數據點分配到最近的簇

• 計算每個數據點與 K 個簇中心的距離（常用歐氏距離，也可根據場景選擇曼哈頓距離等）。
• 將每個數據點分配到?距離最近的簇中心所在的簇，形成 K 個臨時簇。

4.更新簇中心：重新計算每個簇的中心

• 針對步驟 3 中得到的每個簇，計算簇內所有數據點的?均值（即每個特征維度的平均值），將這個均值作為該簇新的簇中心。
• 例如，一個簇包含數據點 (x?,y?)、(x?,y?)、(x?,y?)，則新簇中心為 ((x?+x?+x?)/3, (y?+y?+y?)/3)。

5.判斷是否收斂

• 比較更新后的簇中心與更新前的簇中心：
  • 若所有簇中心的位置變化?小于預設的閾值（如距離變化趨近于 0），則認為聚類收斂，算法終止。
  • 若未收斂，則返回步驟 3，重復 “簇分配→更新簇中心” 的過程，直到滿足收斂條件。

6.輸出聚類結果

• 收斂后，得到最終的 K 個簇及對應的簇中心，每個數據點都被明確分配到一個簇，聚類完成。

示例說明

假設對以下二維數據點進行 K=2 聚類：{(1,1), (1,2), (2,1), (5,5), (6,5), (5,6)}

1. 隨機選擇初始中心：例如 (1,1) 和 (5,5)；
2. 簇分配：(1,1)、(1,2)、(2,1) 距離 (1,1) 更近，歸為簇 1；(5,5)、(6,5)、(5,6) 距離 (5,5) 更近，歸為簇 2；
3. 更新中心：簇 1 新中心為 (1.33, 1.33)，簇 2 新中心為 (5.33, 5.33)；
4. 再次分配：數據點與新中心的距離變化極小，簇分配不變，中心更新后變化趨近于 0，收斂，最終得到兩個明顯分離的簇。

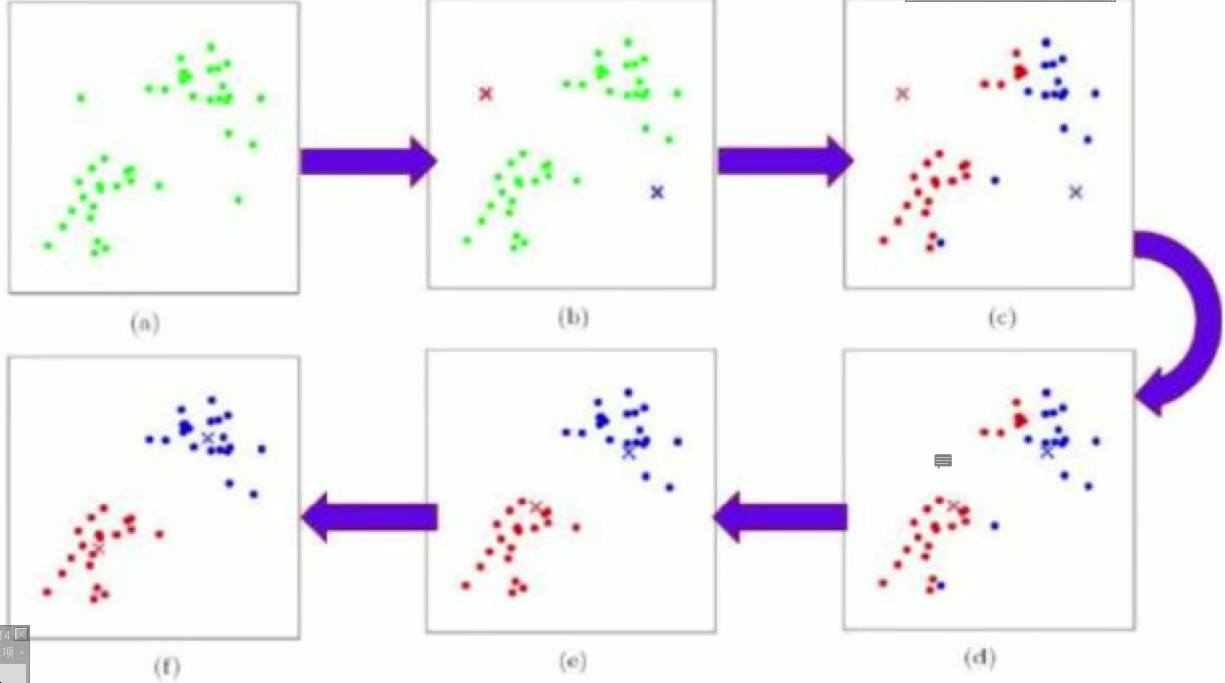
三、聚類效果評價方式

輪廓系數：

• ：對于第i個元素，計算與其同一個簇內所有其他元素距離的平均值，表示了簇內的凝聚程度。
• ：選取外的一個簇，計算與該簇內所有點距離的平均距離，遍歷其他所有簇，取所有平均值中最小的一個，表示簇間的分離度。

計算所有x的輪廓系數，求出平均值即為當前聚類的整體輪廓系數。

1. 輪廓系數范圍在[-1,1]之間。該值越大，越合理。
2. s(i)接近1，則說明樣本i聚類合理；
3. s(i)接近-1，則說明樣本i更應該分類到另外的簇；
4. 若s(i)近似為0，則說明樣本i在兩個簇的邊界上。

四、k-means的API

class sklearn.cluster.KMeans(n_clusters=8,init='k-means++',n_init=10,max_iter=300,tol=0.0001,precompute_distances='auto',verbose=0,random_state=None,copy_x=True,n_jobs=None,algorithm='auto'
)[source]

參數解釋

1. n_clusters：
   • 類型：int，默認值?8
   • 含義：要生成的簇（cluster）的數量，即你希望將數據集劃分成多少個簇 ，比如?n_clusters=3?就是劃分成 3 個簇。
2. init：
   • 類型：str?或?ndarray，默認值?'k-means++'
   • 取值及含義：
     • 'k-means++'：一種智能初始化簇中心的方式，能讓初始簇中心彼此盡可能遠離，一定程度上避免因初始中心選擇不佳導致聚類結果差的問題。
     • 'random'：完全隨機從數據集中選擇初始簇中心。
     • 也可以傳入一個形狀為?(n_clusters, n_features)?的?ndarray，手動指定初始簇中心。
3. n_init：
   • 類型：int，默認值?10
   • 含義：表示運行 K-Means 算法的不同初始簇中心配置的次數。算法會從這些不同的初始配置中，選取使聚類結果（比如簇內距離平方和最小）最優的那一次結果作為最終輸出，增加該值可能提升結果質量，但會增加計算時間 。
4. max_iter：
   • 類型：int，默認值?300
   • 含義：單次 K-Means 算法迭代（包括簇分配、更新簇中心過程）的最大次數，若達到該次數還未收斂（簇中心變化小于?tol?等條件未滿足），則停止迭代 。
5. tol：
   • 類型：float，默認值?0.0001
   • 含義：簇中心變化的容忍度（閾值），當兩次迭代中所有簇中心的變化量都小于該值時，認為算法收斂，停止迭代 。
6. precompute_distances：
   • 類型：str?或?bool，默認值?'auto'
   • 取值及含義：
     • 'auto'：讓算法自動判斷是否預先計算距離矩陣來加速計算，一般小數據集會啟用預計算，大數據集可能不啟用避免內存不足。
     • True：強制預先計算距離矩陣。
     • False：不預先計算距離矩陣，實時計算樣本與簇中心的距離。
7. verbose：
   • 類型：int，默認值?0
   • 含義：控制算法運行時的輸出詳細程度，0?表示不輸出詳細信息，1?及以上會輸出迭代過程中的一些日志（如每次迭代的簇內距離平方和等 ）。
8. random_state：
   • 類型：int、RandomState?實例或?None，默認值?None
   • 含義：用于初始化簇中心的隨機數生成器的種子（當?init='random'?或?init='k-means++'?時起作用 ），設置固定值可讓結果可復現，方便調試和對比實驗。
9. copy_x：
   • 類型：bool，默認值?True
   • 含義：如果為?True，在計算過程中會復制原始數據?X，避免直接修改原始數據；若為?False，可能會在原始數據上進行一些操作（節省內存，但有修改原始數據風險 ）。
10. n_jobs：
    • 類型：int?或?None，默認值?None
    • 含義：用于指定并行運行的作業數量，-1?表示使用所有可用的 CPU 核心并行計算，None?在舊版本?scikit-learn?中通常等價于?1（不并行 ），正數表示使用指定數量的核心，主要用于加速?n_init?過程中多次運行 K-Means 的情況 。
11. algorithm：
    • 類型：str，默認值?'auto'
    • 取值及含義：
      • 'auto'：讓算法自動選擇適合的優化算法（根據數據規模等判斷，小數據用?full?，大數據用?elkan?）。
      • 'full'：使用傳統的 K-Means 算法實現（遍歷計算距離 ）。
      • 'elkan'：利用三角不等式優化距離計算，在數據是稠密且簇分離較好時，計算速度更快，但對稀疏數據支持不好 。

五、案例分析

數據集分析

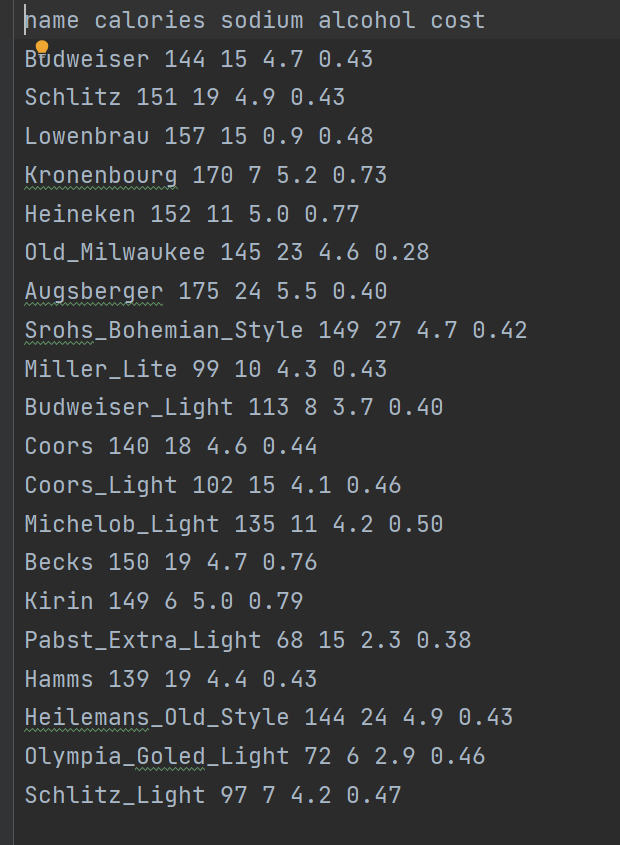
????????關于不同啤酒（或酒類飲品）的數據集，包含啤酒名稱，卡路里，鈉含量，酒精度，成本進行聚類。

1.導入必要的庫

import pandas as pd                  # 用于數據讀取和處理
from sklearn.cluster import KMeans   # 提供K-means聚類算法
from sklearn import metrics          # 提供聚類評估指標（如輪廓系數）
import matplotlib.pyplot as plt      # 用于數據可視化

2. 數據讀取與特征選擇

# 讀取數據文件
beer = pd.read_table("data.txt", sep=' ', encoding='utf8', engine='python')
# 選擇用于聚類的特征列
X = beer[["calories", "sodium", "alcohol", "cost"]]

• 從data.txt文件中讀取數據，假設該文件包含啤酒相關數據
• 選擇了 4 個特征列：卡路里 (calories)、鈉含量 (sodium)、酒精含量 (alcohol) 和成本 (cost) 作為聚類依據

3. 尋找最佳 K 值（聚類數量）

scores = []
for k in range(2, 10):  # 測試K=2到K=9的情況# 訓練K-means模型并獲取聚類標簽labels = KMeans(n_clusters=k).fit(X).labels_# 計算輪廓系數score = metrics.silhouette_score(X, labels)scores.append(score)

• 輪廓系數 (silhouette score) 是評估聚類質量的指標，范圍在 [-1, 1] 之間
• 值越接近 1，表示聚類效果越好（簇內相似度高，簇間差異大）
• 通過循環測試不同 K 值的聚類效果，為后續選擇最佳 K 值做準備

[0.6917656034079486, 0.6731775046455796, 0.5857040721127795, 0.422548733517202, 0.4559182167013377, 0.43776116697963124, 0.38946337473125997, 0.39746405172426014]

4. 可視化不同 K 值的聚類效果

# 打印不同K值對應的輪廓系數
print(scores)# 繪制得分結果
plt.plot(list(range(2, 10)), scores)
plt.xlabel("Number of Clusters Initialized")
plt.ylabel("Silhouette Score")
plt.show()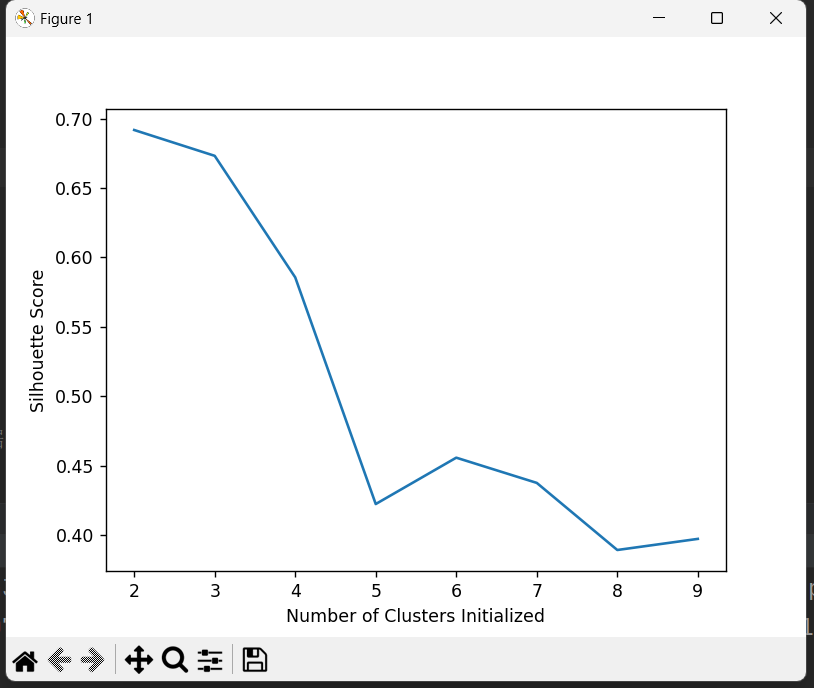

• 打印 K=2 到 K=9 對應的輪廓系數
• 繪制折線圖直觀展示不同 K 值的聚類效果，幫助確定最佳 K 值（通常選擇輪廓系數較高的 K 值）

5. 執行最終聚類

# 選擇K=2進行聚類
km = KMeans(n_clusters=2).fit(X)  # 訓練模型
beer['cluster'] = km.labels_      # 將聚類標簽添加到原數據集

• 根據前面的評估結果，選擇 K=2 進行最終聚類
• 將每個樣本的聚類標簽（0 或 1）添加到原數據集中，方便后續分析

6. 評估最終聚類結果

# 計算最終聚類結果的輪廓系數
score = metrics.silhouette_score(X, beer.cluster)
print(score)

• 單獨計算 K=2 時的輪廓系數并打印
• 這個值可以作為最終聚類效果的量化評估指標

總結

????????K-means 是一種簡潔、高效的聚類且為無監督算法，在數據聚類任務中應用廣泛。它通過持續優化簇中心的位置，逐步收斂并挖掘出數據的聚類結構。不過，該算法對初始設定較為敏感，對簇的形態存在一定限制，更適用于呈球形且分布均勻的簇。