旅游完回來繼續學習。

先來看一下圖論的理論部分，然后稍微做一下DFS的題目。

圖的基本概念

二維坐標中，兩點可以連成線，多個點連成的線就構成了圖。

當然圖也可以就一個節點，甚至沒有節點（空圖）

圖的種類

整體上一般分為 有向圖 和 無向圖。

有向圖是指 圖中邊是有方向的：

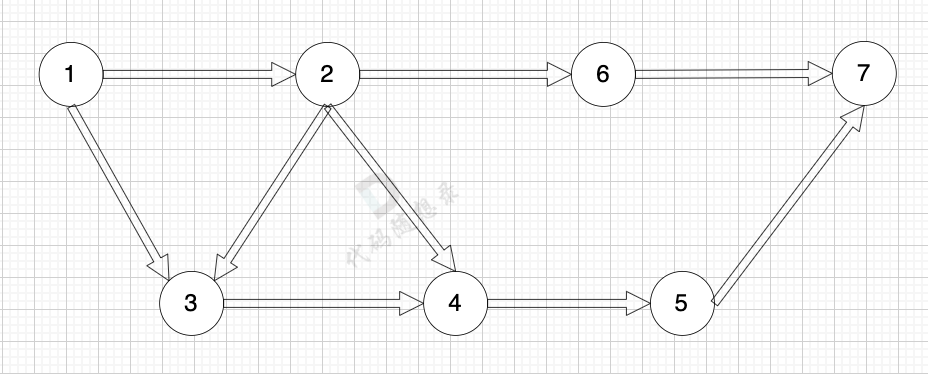無向圖是指 圖中邊沒有方向：

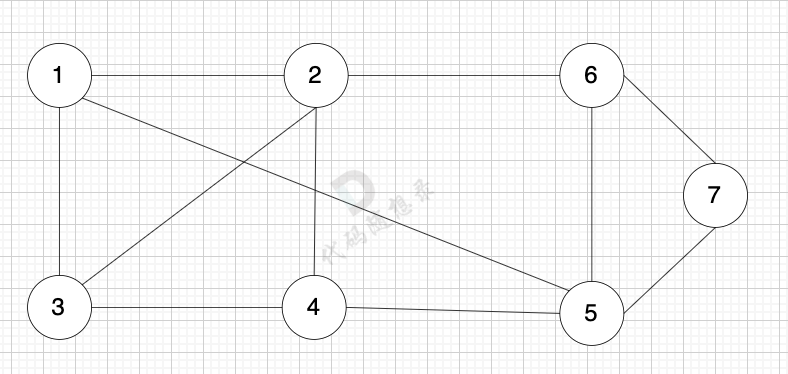加權有向圖，就是圖中邊是有權值的，例如：

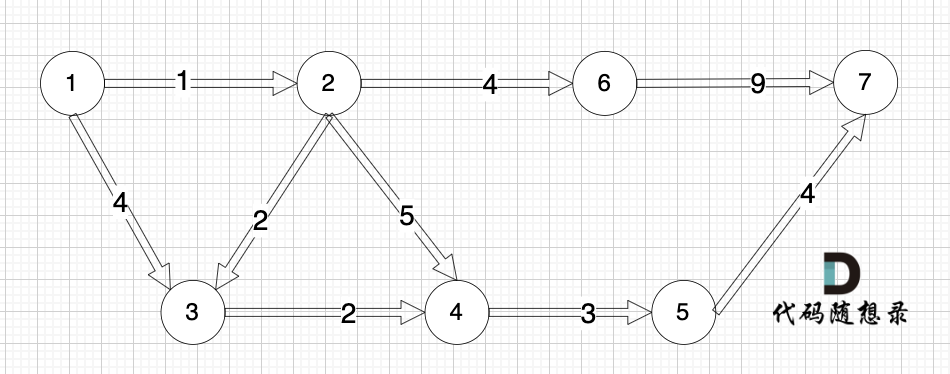加權無向圖也是同理。

度

無向圖中有幾條邊連接該節點，該節點就有幾度。

例如，該無向圖中，節點4的度為5，節點6的度為3。

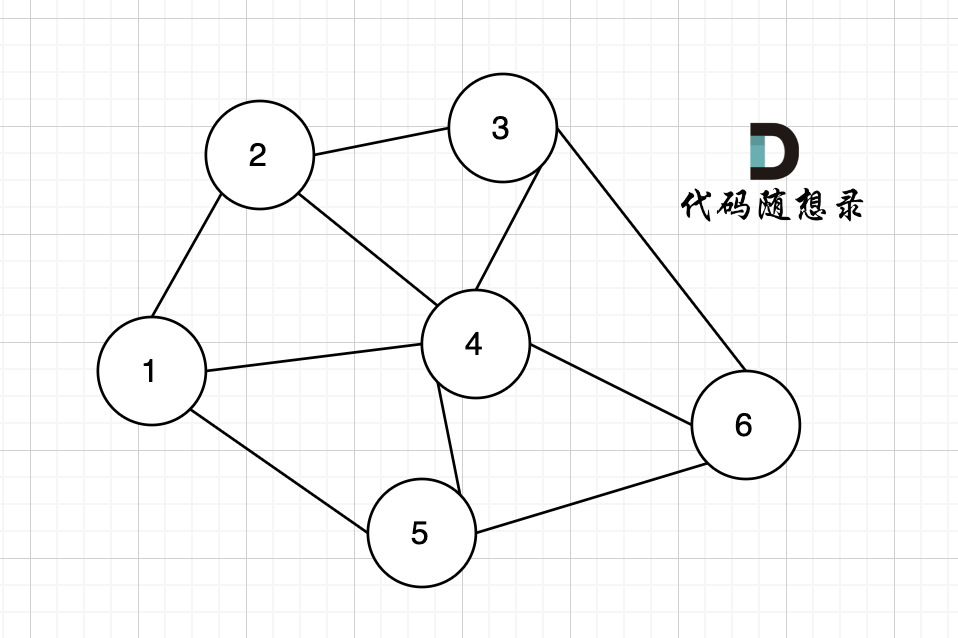在有向圖中，每個節點有出度和入度。

出度：從該節點出發的邊的個數。

入度：指向該節點邊的個數。

例如，該有向圖中，節點3的入度為2，出度為1，節點1的入度為0，出度為2。

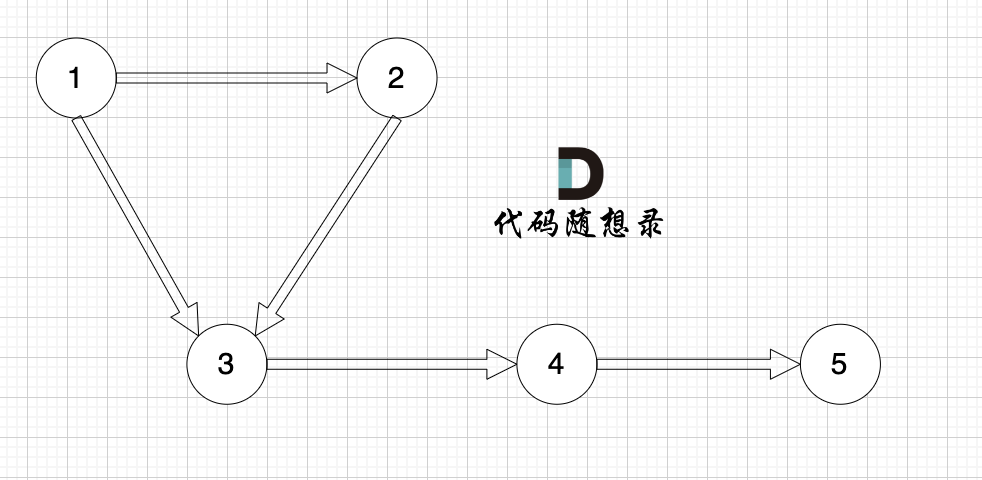連通性

在圖中表示節點的連通情況，我們稱之為連通性。

連通圖

在無向圖中，任何兩個節點都是可以到達的，我們稱之為連通圖 ，如圖：

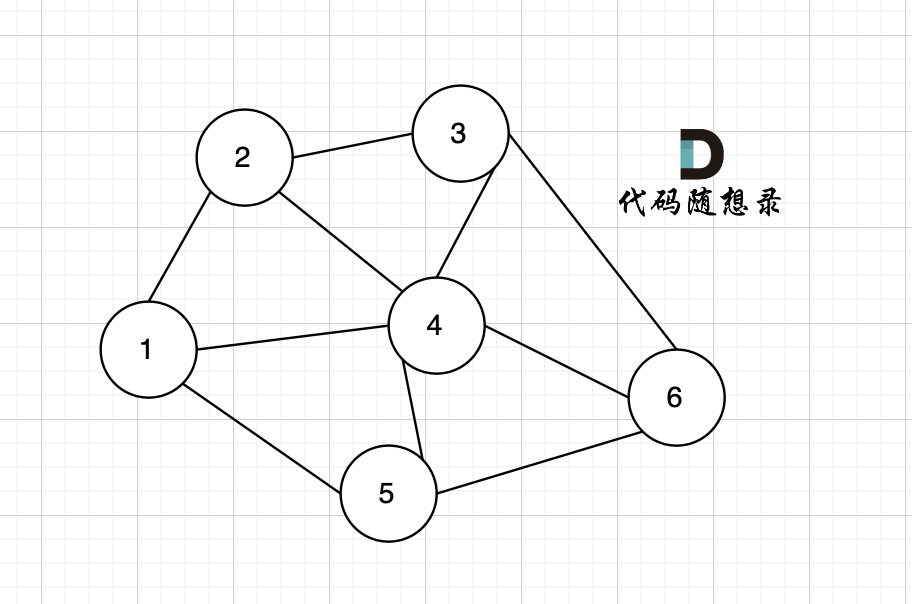如果有節點不能到達其他節點，則為非連通圖，如圖：

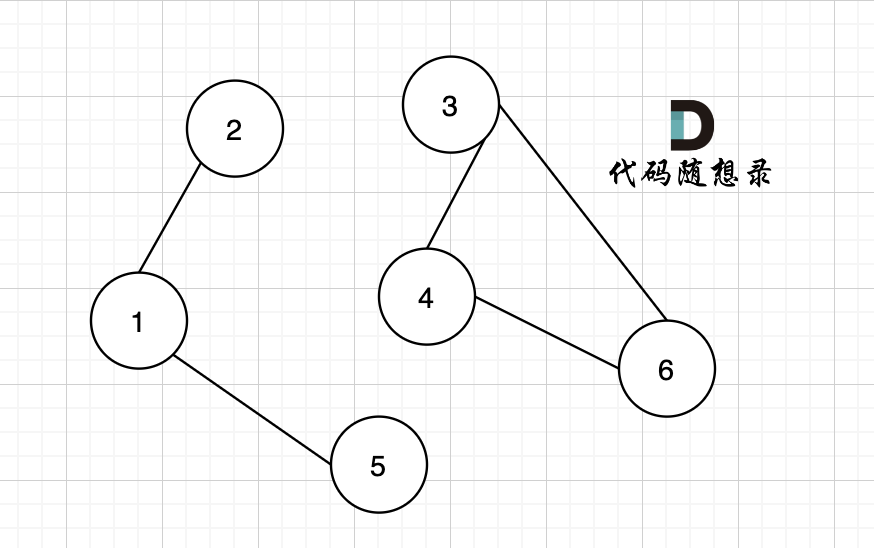節點1 不能到達節點4。

強連通圖

在有向圖中，任何兩個節點是可以相互到達的，我們稱之為 強連通圖。

這里有錄友可能想，這和無向圖中的連通圖有什么區別，不是一樣的嗎？

我們來看這個有向圖：

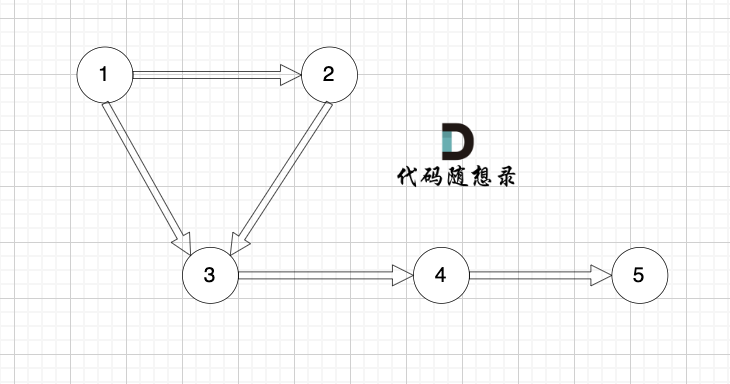這個圖是強連通圖嗎？

初步一看，好像這節點都連著，但這不是強連通圖，節點1可以到節點5，但節點5不能到節點1 。

強連通圖是在有向圖中任何兩個節點是可以相互到達

下面這個有向圖才是強連通圖：

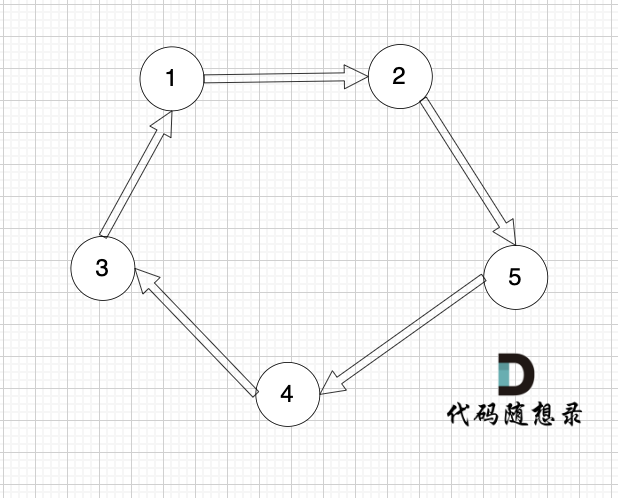連通分量

在無向圖中的極大連通子圖稱之為該圖的一個連通分量。

只看概念大家可能不理解，我來畫個圖：

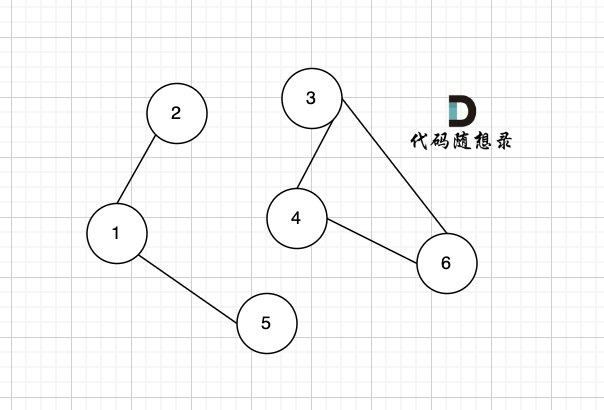該無向圖中 節點1、節點2、節點5 構成的子圖就是 該無向圖中的一個連通分量，該子圖所有節點都是相互可達到的。

同理，節點3、節點4、節點6 構成的子圖 也是該無向圖中的一個連通分量。

那么無向圖中 節點3 、節點4 構成的子圖 是該無向圖的聯通分量嗎？

不是！

因為必須是極大聯通子圖才能是連通分量，所以 必須是節點3、節點4、節點6 構成的子圖才是連通分量。

在圖論中，連通分量是一個很重要的概念，例如島嶼問題（后面章節會有專門講解）其實就是求連通分量。

強連通分量

在有向圖中極大強連通子圖稱之為該圖的強連通分量。

如圖：

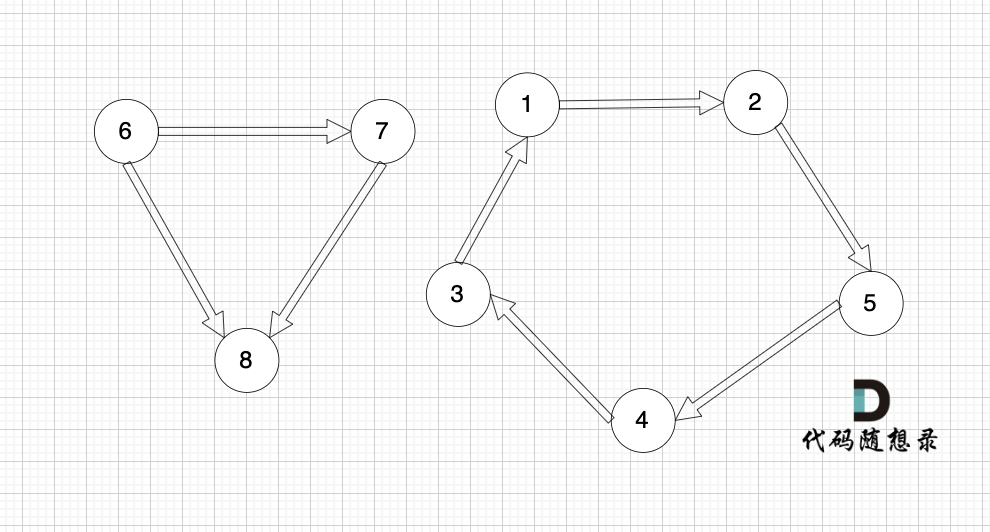節點1、節點2、節點3、節點4、節點5 構成的子圖是強連通分量，因為這是強連通圖，也是極大圖。

節點6、節點7、節點8 構成的子圖 不是強連通分量，因為這不是強連通圖，節點8 不能達到節點6。

節點1、節點2、節點5 構成的子圖 也不是 強連通分量，因為這不是極大圖。

圖的構造

我們如何用代碼來表示一個圖呢？

一般使用鄰接表、鄰接矩陣 或者用類來表示。

主要是 樸素存儲、鄰接表和鄰接矩陣。

關于樸素存儲，這是我自創的名字，因為這種存儲方式，就是將所有邊存下來。

例如圖：

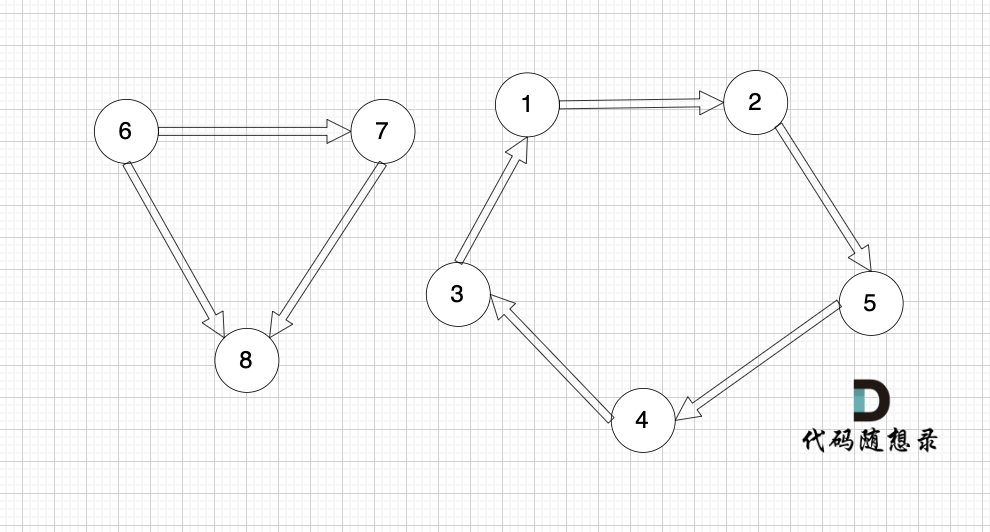圖中有8條邊，我們就定義 8 * 2的數組，即有n條邊就申請n * 2，這么大的數組：

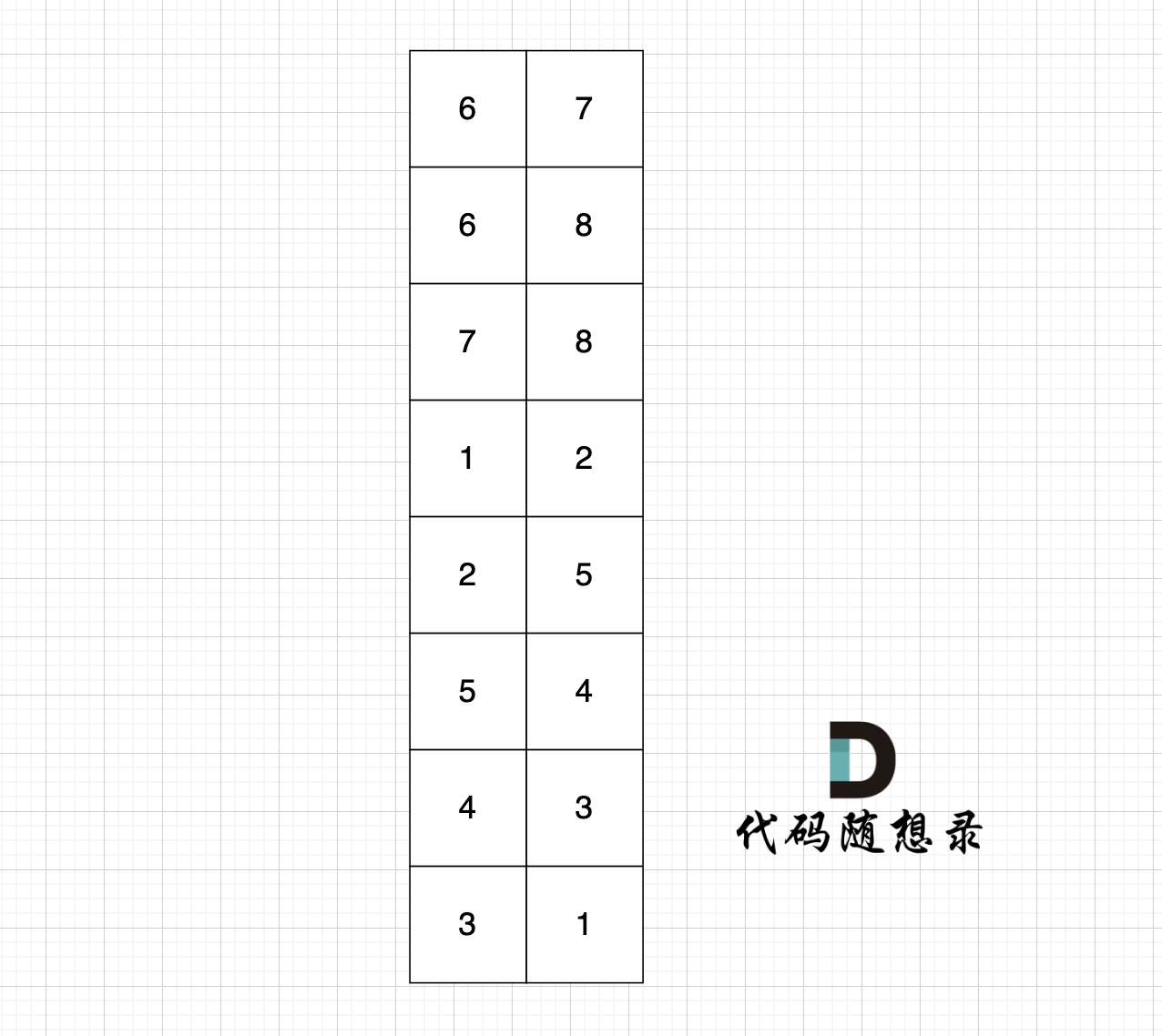數組第一行：6 7，就表示節點6 指向 節點7，以此類推。

當然可以不用數組，用map，或者用 類 到可以表示出 這種邊的關系。

這種表示方式的好處就是直觀，把節點與節點之間關系很容易展現出來。

但如果我們想知道 節點1 和 節點6 是否相連，我們就需要把存儲空間都枚舉一遍才行。

這是明顯的缺點，同時，我們在深搜和廣搜的時候，都不會使用這種存儲方式。

因為 搜索中，需要知道 節點與其他節點的鏈接情況，而這種樸素存儲，都需要全部枚舉才知道鏈接情況。

在圖論章節的后面文章講解中，我會舉例說明的。大家先有個印象。

鄰接矩陣

鄰接矩陣 使用 二維數組來表示圖結構。 鄰接矩陣是從節點的角度來表示圖，有多少節點就申請多大的二維數組。

例如： grid[2][5] = 6，表示 節點 2 連接 節點5 為有向圖，節點2 指向 節點5，邊的權值為6。

如果想表示無向圖，即：grid[2][5] = 6，grid[5][2] = 6，表示節點2 與 節點5 相互連通，權值為6。

如圖：

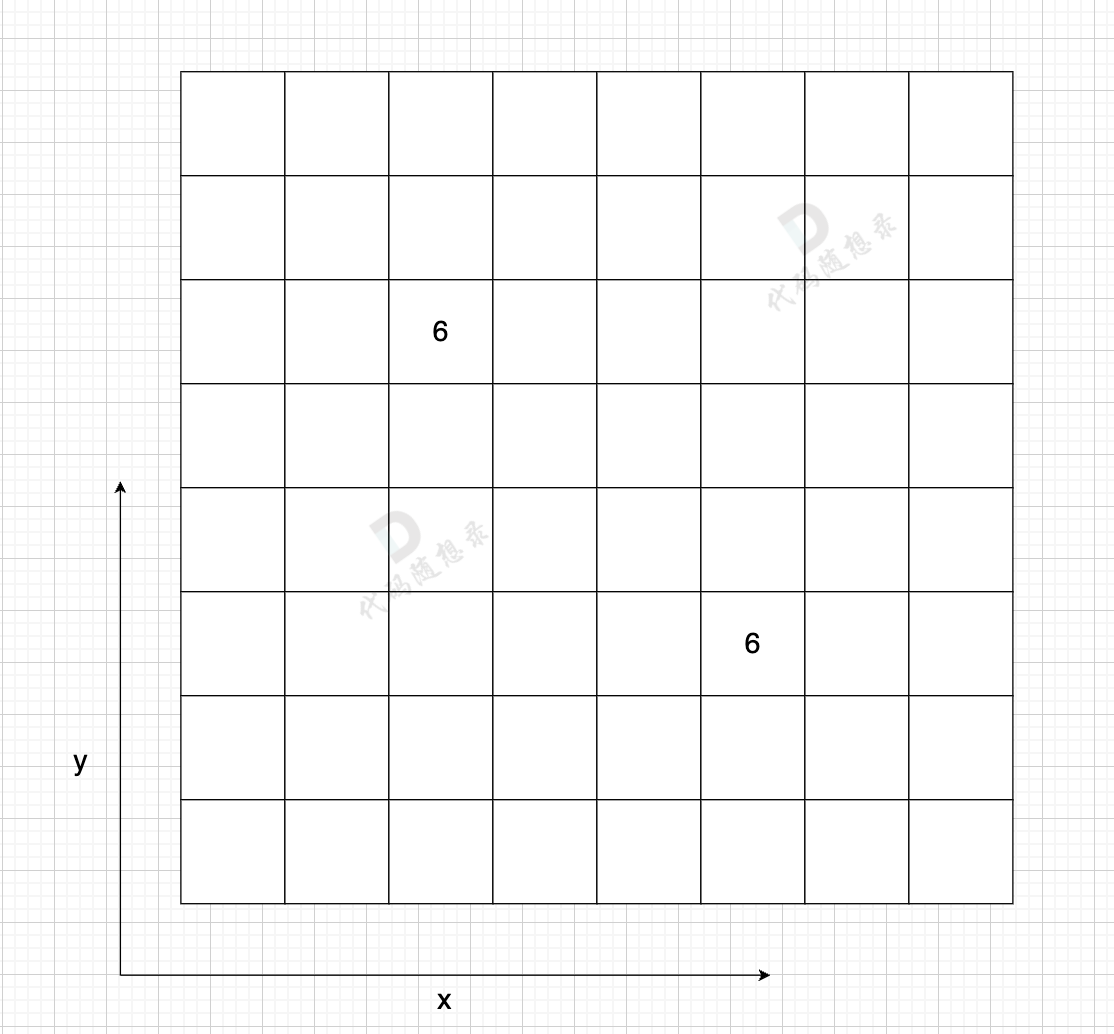在一個 n （節點數）為8 的圖中，就需要申請 8 * 8 這么大的空間。

圖中有一條雙向邊，即：grid[2][5] = 6，grid[5][2] = 6

這種表達方式（鄰接矩陣） 在 邊少，節點多的情況下，會導致申請過大的二維數組，造成空間浪費。

而且在尋找節點連接情況的時候，需要遍歷整個矩陣，即 n * n 的時間復雜度，同樣造成時間浪費。

鄰接矩陣的優點：

• 表達方式簡單，易于理解
• 檢查任意兩個頂點間是否存在邊的操作非常快
• 適合稠密圖，在邊數接近頂點數平方的圖中，鄰接矩陣是一種空間效率較高的表示方法。

缺點：

• 遇到稀疏圖，會導致申請過大的二維數組造成空間浪費 且遍歷 邊 的時候需要遍歷整個n * n矩陣，造成時間浪費

鄰接表

鄰接表 使用 數組 + 鏈表的方式來表示。 鄰接表是從邊的數量來表示圖，有多少邊 才會申請對應大小的鏈表。

鄰接表的構造如圖：

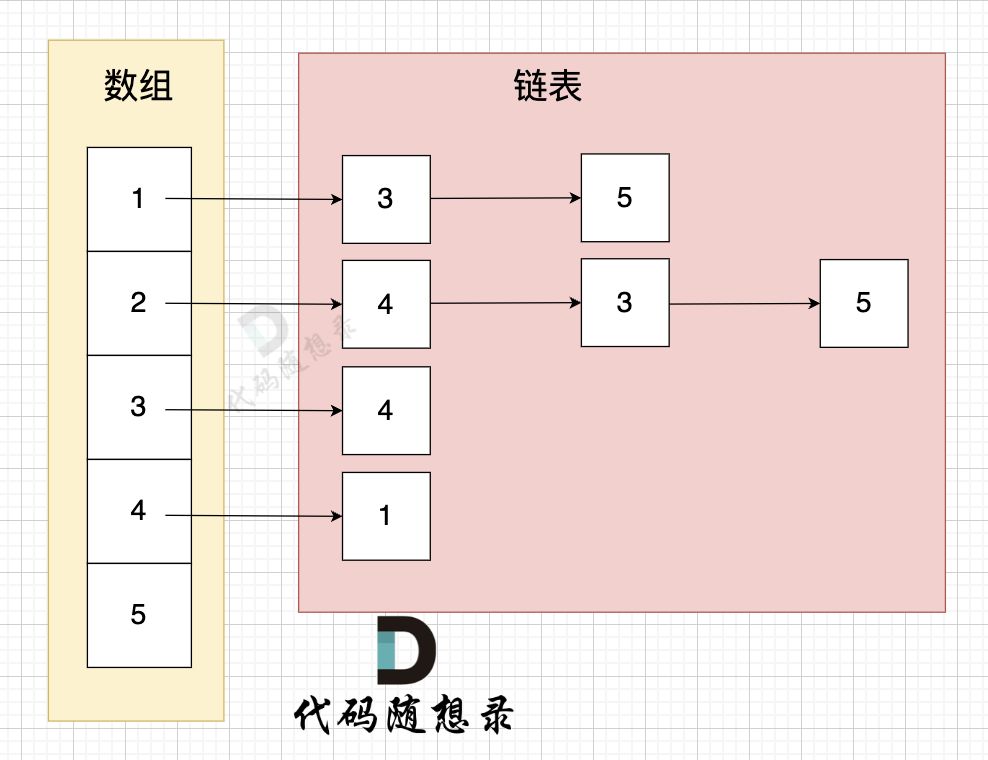這里表達的圖是：

• 節點1 指向 節點3 和 節點5
• 節點2 指向 節點4、節點3、節點5
• 節點3 指向 節點4
• 節點4指向節點1

有多少邊 鄰接表才會申請多少個對應的鏈表節點。

從圖中可以直觀看出 使用 數組 + 鏈表 來表達 邊的連接情況 。

鄰接表的優點：

• 對于稀疏圖的存儲，只需要存儲邊，空間利用率高
• 遍歷節點連接情況相對容易

缺點：

• 檢查任意兩個節點間是否存在邊，效率相對低，需要 O(V)時間，V表示某節點連接其他節點的數量。
• 實現相對復雜，不易理解

以上大家可能理解比較模糊，沒關系，因為大家還沒做過圖論的題目，對于圖的表達沒有概念。

這里我先不給出具體的實現代碼，大家先有個初步印象，在后面算法題實戰中，我還會講到具體代碼實現，等帶大家做算法題，寫了代碼之后，自然就理解了。

圖的遍歷方式

圖的遍歷方式基本是兩大類：

• 深度優先搜索（dfs）
• 廣度優先搜索（bfs）

二叉樹的遞歸遍歷，是dfs 在二叉樹上的遍歷方式。

二叉樹的層序遍歷，是bfs 在二叉樹上的遍歷方式。

dfs 和 bfs 一種搜索算法，可以在不同的數據結構上進行搜索，在二叉樹章節里是在二叉樹這樣的數據結構上搜索。

而在圖論章節，則是在圖（鄰接表或鄰接矩陣）上進行搜索。

然后來看一道題目：98. 所有可達路徑

這道題需要找出所有的路徑，很明顯是一道深搜的題目。

而對于深搜的題目來講，最重要的就是搞清楚遞歸的參數，條件，終止情況

但是，由于這里是ACM模式，所以我們還需要注意數據的讀取和存儲，其實這道題存儲量不大，三種圖的存儲方式都是可以的。但是寫法也會發生變化，下面把三種方式都放出來。

鄰接矩陣寫法

#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> result; // 收集符合條件的路徑
vector<int> path; // 1節點到終點的路徑void dfs (const vector<vector<int>>& graph, int x, int n) {// 當前遍歷的節點x 到達節點n if (x == n) { // 找到符合條件的一條路徑result.push_back(path);return;}for (int i = 1; i <= n; i++) { // 遍歷節點x鏈接的所有節點if (graph[x][i] == 1) { // 找到 x鏈接的節點path.push_back(i); // 遍歷到的節點加入到路徑中來dfs(graph, i, n); // 進入下一層遞歸path.pop_back(); // 回溯，撤銷本節點}}
}int main() {int n, m, s, t;cin >> n >> m;// 節點編號從1到n，所以申請 n+1 這么大的數組vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));while (m--) {cin >> s >> t;// 使用鄰接矩陣 表示無線圖，1 表示 s 與 t 是相連的graph[s][t] = 1;}path.push_back(1); // 無論什么路徑已經是從0節點出發dfs(graph, 1, n); // 開始遍歷// 輸出結果if (result.size() == 0) cout << -1 << endl;for (const vector<int> &pa : result) {for (int i = 0; i < pa.size() - 1; i++) {cout << pa[i] << " ";}cout << pa[pa.size() - 1]  << endl;}
}

鄰接表寫法

#include <iostream>
#include <vector>
#include <list>
using namespace std;vector<vector<int>> result; // 收集符合條件的路徑
vector<int> path; // 1節點到終點的路徑void dfs (const vector<list<int>>& graph, int x, int n) {if (x == n) { // 找到符合條件的一條路徑result.push_back(path);return;}for (int i : graph[x]) { // 找到 x指向的節點path.push_back(i); // 遍歷到的節點加入到路徑中來dfs(graph, i, n); // 進入下一層遞歸path.pop_back(); // 回溯，撤銷本節點}
}int main() {int n, m, s, t;cin >> n >> m;// 節點編號從1到n，所以申請 n+1 這么大的數組vector<list<int>> graph(n + 1); // 鄰接表while (m--) {cin >> s >> t;// 使用鄰接表 ，表示 s -> t 是相連的graph[s].push_back(t);}path.push_back(1); // 無論什么路徑已經是從0節點出發dfs(graph, 1, n); // 開始遍歷// 輸出結果if (result.size() == 0) cout << -1 << endl;for (const vector<int> &pa : result) {for (int i = 0; i < pa.size() - 1; i++) {cout << pa[i] << " ";}cout << pa[pa.size() - 1]  << endl;}
}

下面是筆者自己寫的樸素存儲的方式：

#include<iostream>
#include<vector>
using namespace std;vector<vector<int>> path;
vector<int> pre_path;void dfs(vector<pair<int,int>> ab,int i,int n){if(i==n){path.push_back(pre_path);return;}for(auto pre:ab){int k=0;if(pre.first==i)    k=pre.second;pre_path.push_back(k);dfs(ab,k,n);pre_path.pop_back();}
}int main(){int n,m=0;cin>>n>>m;vector<pair<int,int>>   ab(m,{0,0});for(int i=0;i<m;i++){cin>>ab[i].first>>ab[i].second;}pre_path.push_back(1);dfs(ab,1,n);if (path.size() == 0) cout << -1 << endl;for (const vector<int> &pa : path) {for (int i = 0; i < pa.size() - 1; i++) {cout << pa[i] << " ";}cout << pa[pa.size() - 1]  << endl;}
}

OK，今天就到這