D-小紅的矩陣不動點_牛客周賽 Round 104

賽時這道題卡了一段時間，賽時代碼如下：

#include<bits/stdc++.h>
using namespace std;
int ans,h;
int a[505][505];
signed main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int n,m;cin>>n>>m;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){cin>>a[i][j];if(a[i][j]==min(i,j))ans++;}if(ans==n*m){cout<<ans;return 0;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]>=1&&a[i][j]<=min(n,m)){int t=a[i][j],c=min(i,j),v=a[t][t];//要想成為不動點，可以換到(t,t)~(t,m) or (t,t)~(n,t)//換過來成為不動點，要求值滿足v==cif(i!=t||j!=t){if(v==c&&v==t)h=max(h,1);else if(v==c&&v!=t)h=2;else if(v!=c&&v!=t)h=max(h,1);else if(v!=c&&v==t)h=max(h,0);}for(int k=t+1;k<=m;k++){if(i!=t||j!=k){v=a[t][k];if(v==c&&v==t)h=max(h,1);else if(v==c&&v!=t)h=2;else if(v!=c&&v!=t)h=max(h,1);else if(v!=c&&v==t)h=max(h,0);}}for(int k=t+1;k<=n;k++){if(i!=k||j!=t){v=a[k][t];if(v==c&&v==t)h=max(h,1);else if(v==c&&v!=t)h=2;else if(v!=c&&v!=t)h=max(h,1);else if(v!=c&&v==t)h=max(h,0);}}}}}cout<<min(ans+h,n*m);return 0;
}

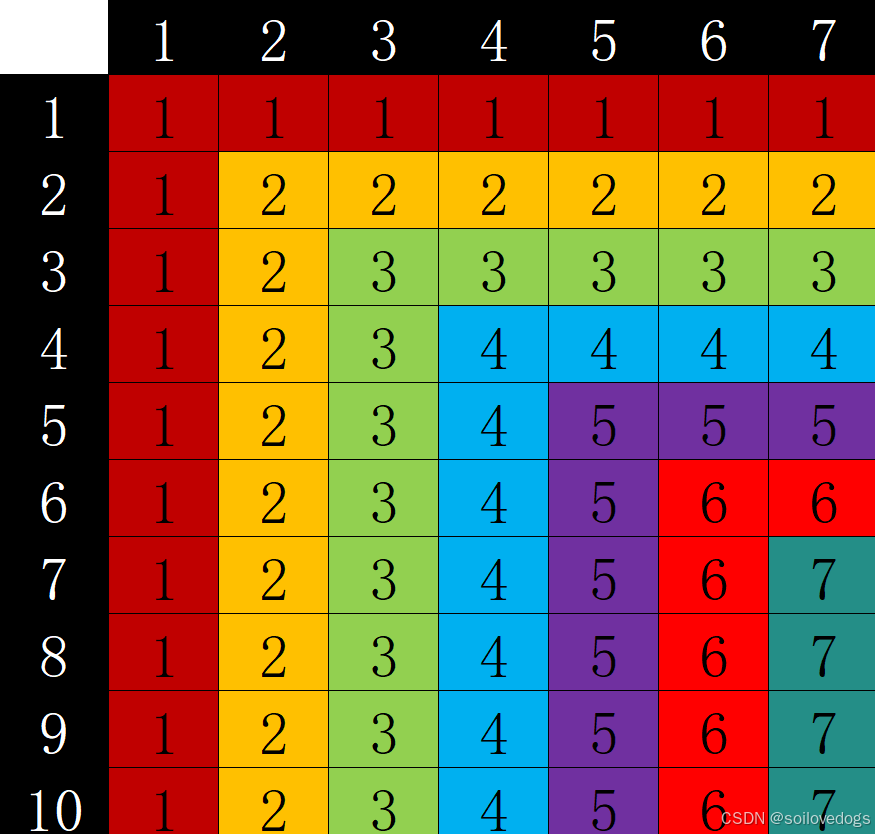
上面這張圖，以10?7矩陣為例，表示每個點要是不動點需要的值。

我們考慮一下所有增加不動點數量的交換方式。

初步思考，可能增加不動點數量的交換無非三種情況：

1. 兩個非不動點->一個不動點，一個非不動點 不動點數+1
2. 兩個非不動點->兩個不動點 不動點數+2
3. 一個不動點，一個非不動點->兩個不動點 不動點數+1

第一種情況如下圖：

第二種情況如下圖：

如果遇到第二種情況，可以直接斷定這就是最優方案，不用再繼續下去了。

第三種情況，我們細想一下，兩個位置如果在“同一色塊”，明顯不成立，那么兩個位置只能在“不同色塊”，但是，這樣也不成立，因為之前的不動點必然會變成非不動點，故這種情況并不存在。

也就是說，我們總共只有兩種可能：

1. 兩個非不動點->一個不動點，一個非不動點 不動點數+1
2. 兩個非不動點->兩個不動點 不動點數+2

現在我們再仔細討論一下這種情況的代碼具體實現思路。

等一下，先到這里，我要去思考一下了。

---

好了，我又回來了。首先，兩種情況討論的都是非不動點，我們需要一個高效的結構去存儲非不動點的信息。

就拿示例2來說吧。

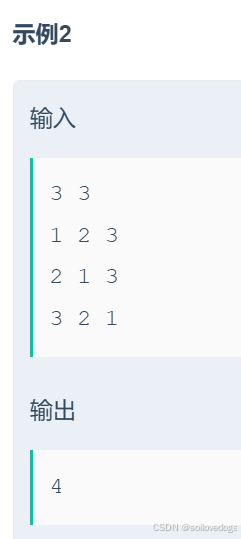
我改了一下代碼，通過了88.89%。

#include<bits/stdc++.h>
using namespace std;
int ans,h;
int a[505][505];
set<int> v[505];
signed main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int n,m;cin>>n>>m;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){cin>>a[i][j];if(a[i][j]==min(i,j))ans++;else v[min(i,j)].insert(a[i][j]);}for(int i=1;i<=min(n,m);i++){for(int e:v[i]){if(v[e].count(i)){h=2;break;}else h=1;}if(h==2)break;}cout<<ans+h;return 0;
}

---

剛又調了一下，終于過了！

#include<bits/stdc++.h>
using namespace std;
int ans,h;
int a[505][505];
set<int> v[505];
signed main(){ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int n,m;cin>>n>>m;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){cin>>a[i][j];if(a[i][j]==min(i,j))ans++;else v[min(i,j)].insert(a[i][j]);}for(int i=1;i<=min(n,m);i++){for(int e:v[i]){if(v[e].count(i)){h=2;break;}else if(v[e].size())h=1;}if(h==2)break;}cout<<ans+h;return 0;
}

參考：【題解】牛客周賽 Round 104_ICPC/CCPC/NOIP/NOI刷題訓練題單_牛客競賽OJ