回歸是科研中最常見的統計學研究方法之一,在研究變量間關系方面有著極其廣泛的應用。由于其基本假設的限制,包括線性回歸及廣義線性回歸在內的各種常見的回歸方法都有三個重大缺陷:(1)對于異常值非常敏感,極少量的異常值可能導致結果產生巨大的誤差;(2)對數據的分布有著較為苛刻的要求,如果數據不符合指定的分布,結果同樣是不可信的;(3)只能估計因變量的條件均值,不能估計自變量對因變量分位點的不同影響。分位數回歸的出現較好的解決了第(1)和第(3)個問題,對不同分布數據也表現非常好的穩定性。
一:線性回歸假設與分位數函數
1.線性回歸的本質
2.線性回歸的基本假設
3.最小二乘法與極大似然法4.線性回歸的推廣與分位數函數
二:線性分位數回歸【代碼實踐】
1.最小一乘法及其推廣
2.分位數回歸結果的解釋
3.顯著性檢驗
4.分位數回歸的擬合優度檢驗?
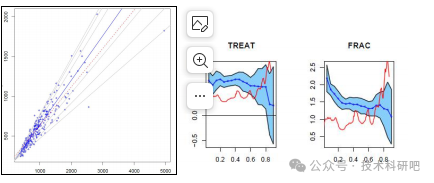
三:貝葉斯分位數回歸【代碼實踐】
1.貝葉斯統計學的基本概念
2.非對稱拉普拉斯先驗
3.貝葉斯分位數回歸
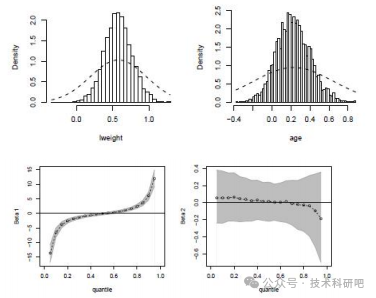
四:超越線性分位數回歸(一)【代碼實踐】
1.非線性分位數回歸
2.非參數分位數回歸
3.廣義分位數回歸及其貝葉斯版本
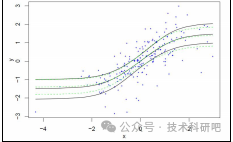
五:超越線性分位數回歸(二)【代碼實踐】
1.線性分位數混合效應模型
2.CDF-分位數回歸
3.分位數隨機森林
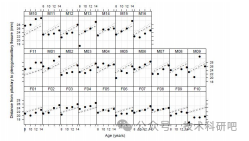
)












-day28)
?)




Extent 介紹)