主要內容：
整除的基本概念（掌握）
素數（掌握）
同余的概念（掌握）
1.1整除
定義：設a，b是任意兩個整數，其中b≠0，如果存在一個整數q，使 a = qb，則我們稱b整除a，或a被b整除，記為b|a，此時稱 b是a的因子，a是b的倍數。
例：a=10, b=2則有2|10；若a=100, b=10有10|100
例：設a是整數，a≠0, 則a|0。
整除的基本性質：
1. 如果b|a且a|b，則b = a或b = -a。
2. 如果a|b且b|c，則a|c。
3. 如果c|a且c|b，則c|ua+vb，其中u，v是整數。
整除的基本性質（補充）：
(1)?a|b<=>-a|b<=>a|-b<=>-a|-b<=>|a| | |b|
(2) b≠0且a|b => |a|≤|b|
帶余除法：當兩個整數不能整除時，我們有帶余除法：
定義：對于a，b兩個整數，其中b≠0，則存在唯一q，r使得：a=bq+r，0 ≤ r<|b|。r稱為a被b除得到的余數, 當r = 0時，b|a。
例：
1）a = –37， b= 5，則–37 = (-8)×5+3，q=8，r=3
2）a = 67，b= 7，則67=(9)×(7)+4，q=9， r=4
最大公因子：
定義：
1) 設a，b是兩個整數，如果整數c|a且c|b，則c稱為a，b的公因子。
2) 設c>0是兩個不全為零的整數a，b的公因子，如果a，b的任何公因子都整除c，則c稱為a，b的最大公因子，記為c=(a,b)。
最大公因子性質：
1.(a,b)=(-a,b)=(a,-b)=(-a,-b)=(|a|,|b|)
2.(0,a)=a
最大公因子（求解）
例：(-3824，1837)
最大公因子定理：
定理：設a，b是兩個不全為零的整數，則存在兩個整數u, v，使得：(a, b)=ua+vb。
例：將a = 888，b = 312的最大公因子表示為(a,b) = ua+vb。
1.2互素?
定義：設a，b是兩個不全為0的整數，如果(a, b)=1，則稱a，b互素。
推論：a, b互素的充分必要條件是：存在u，v，使ua+vb=1。
互素性質：
1) 如果c|ab且(c, a) = 1，則c|b 。
2) 如果a|c，b|c，且(a, b) = 1，則ab|c 。
3) 如果(a,c) = 1，(b,c) = 1，則(ab,c) =1 。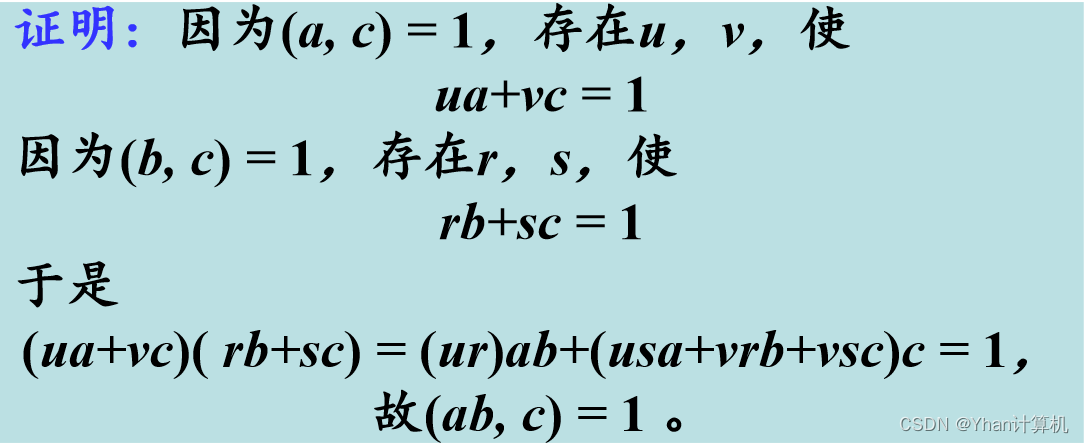
最小公倍數：
定義：
1) 設a, b是兩個不等于零的整數．如果a|d，b|d，則稱d是a和b的公倍數。
2) a和b的正公倍數中最小的稱為a和b的最小公倍數，記為[a,b] 。
最小公倍數性質：
[a，b] = [–a，b] = [a，–b] = [–a，–b] = [|a|，|b|]
例：a = 2，b = 3．它們的公倍數集合為{0，±6，±12，±18，…}.而[2，3] = 6 。
最小公倍數與最大公因子關系：
定理：
1) 設d是a，b的任意公倍數，則[a, b] | d 。
2)
，特別地，如果(a, b) = 1, [a, b] = |ab|。
1.3素數
定義：如果一個大于1的整數p除±1和±p外無其他因子，則p稱為一個素數，否則稱為合數。
定理：設p是一個素數，則
1) 對任意整數a，如果p不整除a，則(p，a) = 1。
2) 如果p|ab，則p|a，或p|b。
算術基本定理：
定理：每個大于1的整數a都可以分解為有限個素數的乘積：a=p1p2…pr。該分解除素數因子的排列外是唯一的。
標準因子分解式：
由于p1，p2，…，pr中可能存在重復，所以a的分解式可表示為有限個素數的冪的乘積：
，這稱為a的標準因子分解式。
例：2100的標準因子分解式：
素數無窮個：
定理：素數有無窮多個。
Eratosthenes篩法：
定理：設a是任意大于1的整數，則a的除1外最小正因子q是一素數，并且當a是一合數時，
。
對于一般N，Eratosthenes篩法可表述如下：
第1步 找出的全部
素數：p1，p2，…，pm。
第2步 在1~N中分別劃去p1，p2，…，pm全部倍數。
第2步完成后剩下的數除1外就是不超過N的全部素數。
篩法原理如下：對于一個數a≤N，如果p1，p2，…，pm都不整除a，則a是素數。這是因為如果a是合數，則由定理它必有一素因子在p1，p2，…，pm中。
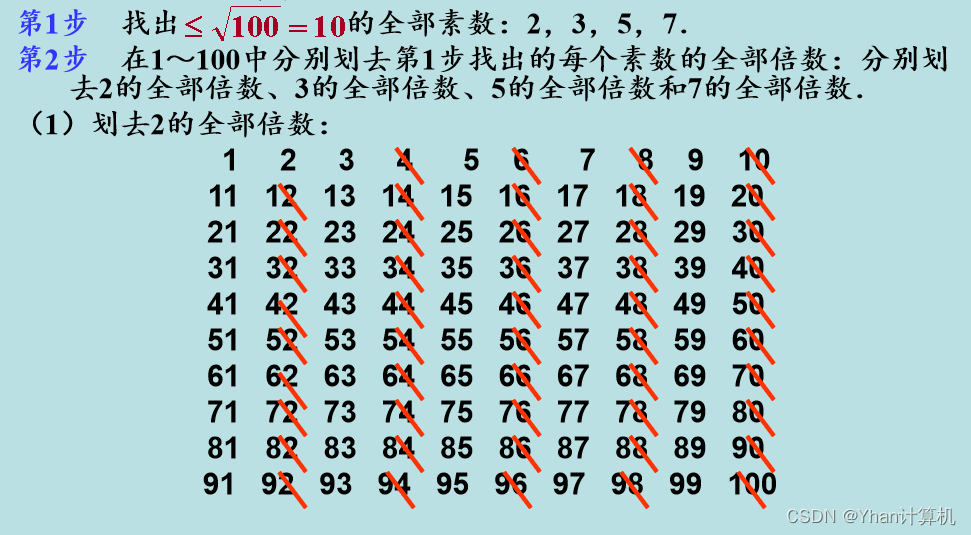
例：求不超過100的全部素數。
同理可以將因子5，7的倍數劃去： (3) 劃去5的全部倍數： (4) 劃去7的全部倍數。
最終經過上述步驟后剩下的數除1外就是不超過100的全部素 數： (25個) ? ?2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97
1.4 同余
定義：給定一個稱為模的正整數m。如果m除整數a，b得相同的余數，即a=q1m+r，b=q2m+r，0≤ r小于等于m， 則稱a和b關于模m同余，記為 a≡b (mod m)
例：25≡1(mod 8)，16≡-5(mod 7)。
定理：整數a，b對模m同余的充分必要條件是：m|(a-b)，即a = b+mt，t是整數。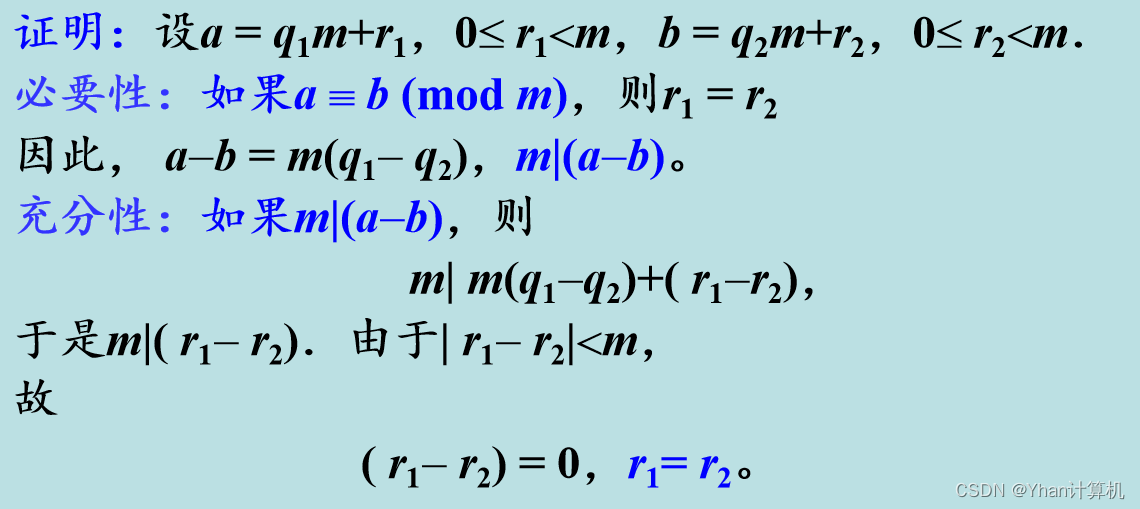
同余性質及推論：
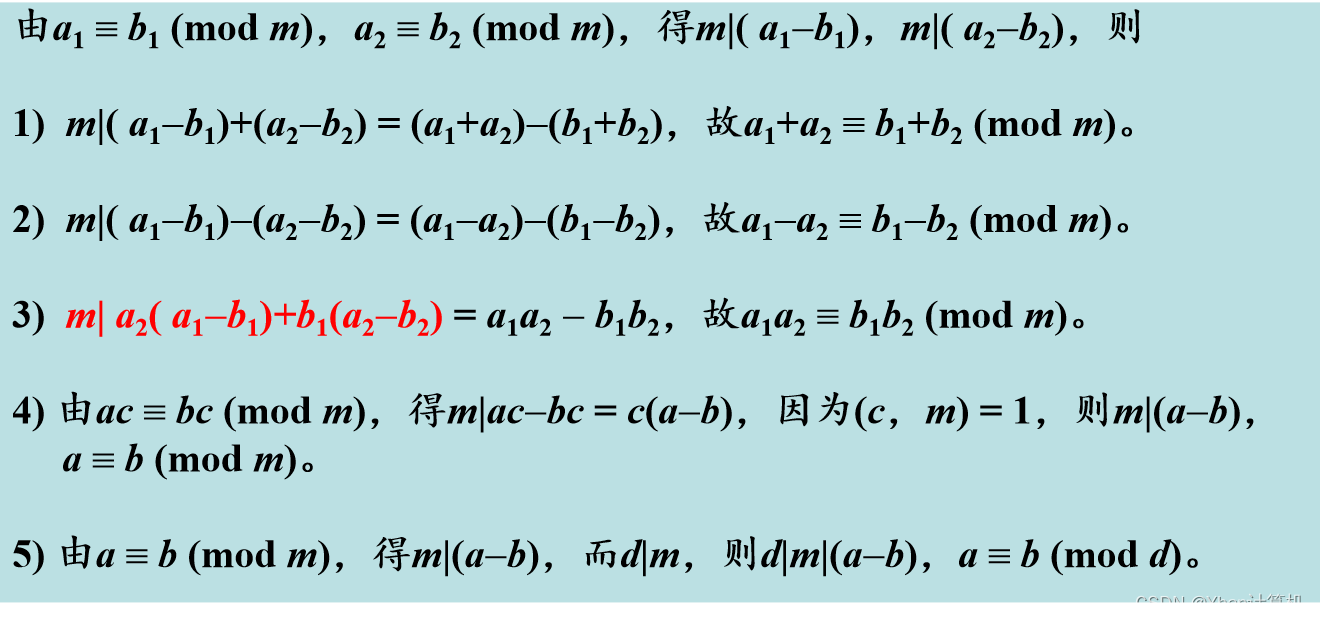
推論：如果a1≡b1 (mod m)，a2≡b2 (mod m)，則：
快速指數算法
例1-16：求解 2^64 (mod 641)
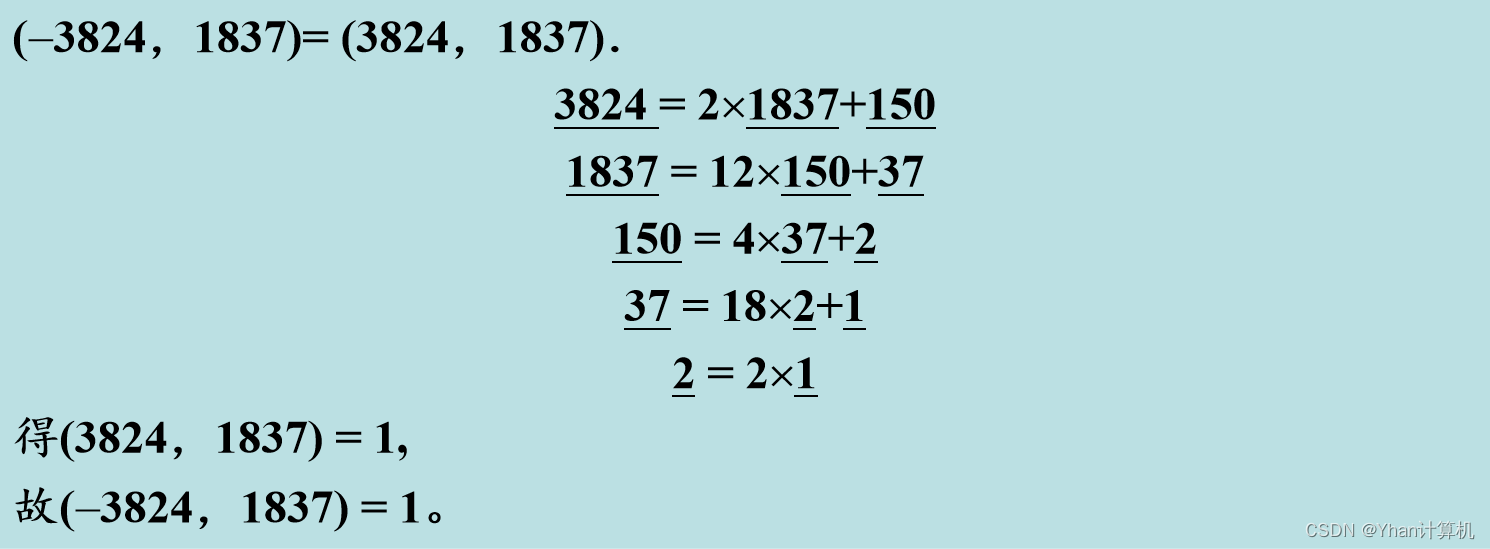
