【數據結構與算法篇】二叉樹鏈式結構及實現

🥕個人主頁:開敲🍉
🔥所屬專欄:每日刷題🍍
🌼文章目錄🌼
4. 二叉樹鏈式結構的實現
? ? 4.1 前置說明
? ? 4.2 二叉樹的遍歷
? ? ? ??4.2.1 前序、中序以及后序遍歷
? ? ? ? 4.2.2 層序遍歷
? ? 4.3 結點個數及高度等
? ? 4.4 二叉樹基礎OJ聯系
? ? 4.5 二叉樹的創建和銷毀

4. 二叉樹鏈式結構的實現
? ? 4.1 前置說明
??在學習二叉樹的基本操作前,需先要創建一棵二叉樹,然后才能學習其相關的基本操作。由于現在大家對二叉樹結構掌握還不夠深入,為了降低大家學習成本,此處手動快速創建一棵簡單的二叉樹,快速進入二叉樹操作學習,等二叉樹結構了解的差不多時,我們反過頭再來研究二叉樹真正的創建方式。
typedef int BTDataType;
typedef struct BinaryTreeNode
{
? ? ? BTDataType _data;
? ? ? struct BinaryTreeNode* _left;
? ? ? struct BinaryTreeNode* _right;
? ? ? }BTNode;
BTNode* CreatBinaryTree()
{
? ? BTNode* node1 = BuyNode(1);
? ? BTNode* node2 = BuyNode(2);
? ? BTNode* node3 = BuyNode(3);
? ? BTNode* node4 = BuyNode(4);
? ? BTNode* node5 = BuyNode(5);
? ? BTNode* node6 = BuyNode(6);
? ? node1->_left = node2;
? ? node1->_right = node4;
? ? node2->_left = node3;
? ? node4->_left = node5;
? ? node4->_right = node6;
? ? return node1;
}
注意:上述代碼并不是創建二叉樹的方式,真正創建二叉樹方式后序詳解重點講解。
再看二叉樹基本操作前,再回顧下二叉樹的概念,二叉樹是:
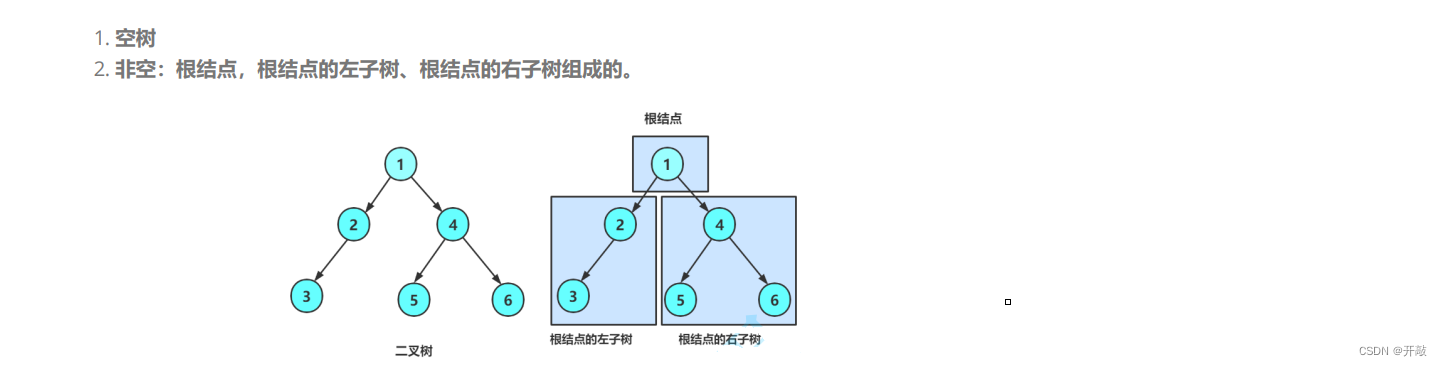
從概念中可以看出,二叉樹定義是遞歸式的,因此后序基本操作中基本都是按照該概念實現的。
? ? 4.2 二叉樹的遍歷
? ? ? ??4.2.1 前序、中序以及后序遍歷
??學習二叉樹結構,最簡單的方式就是遍歷。所謂二叉樹遍歷(Traversal)是按照某種特定的規則,依次對二叉樹中的結點進行相應的操作,并且每個結點只操作一次。訪問結點所做的操作依賴于具體的應用問題。 遍歷是二叉樹上最重要的運算之一,也是二叉樹上進行其它運算的基礎。
??按照規則,二叉樹的遍歷有:前序/中序/后序的遞歸結構遍歷:
? ① 前序:對于每個結點,都滿足 根 一> 左子樹 一> 右子樹 的遍歷順序
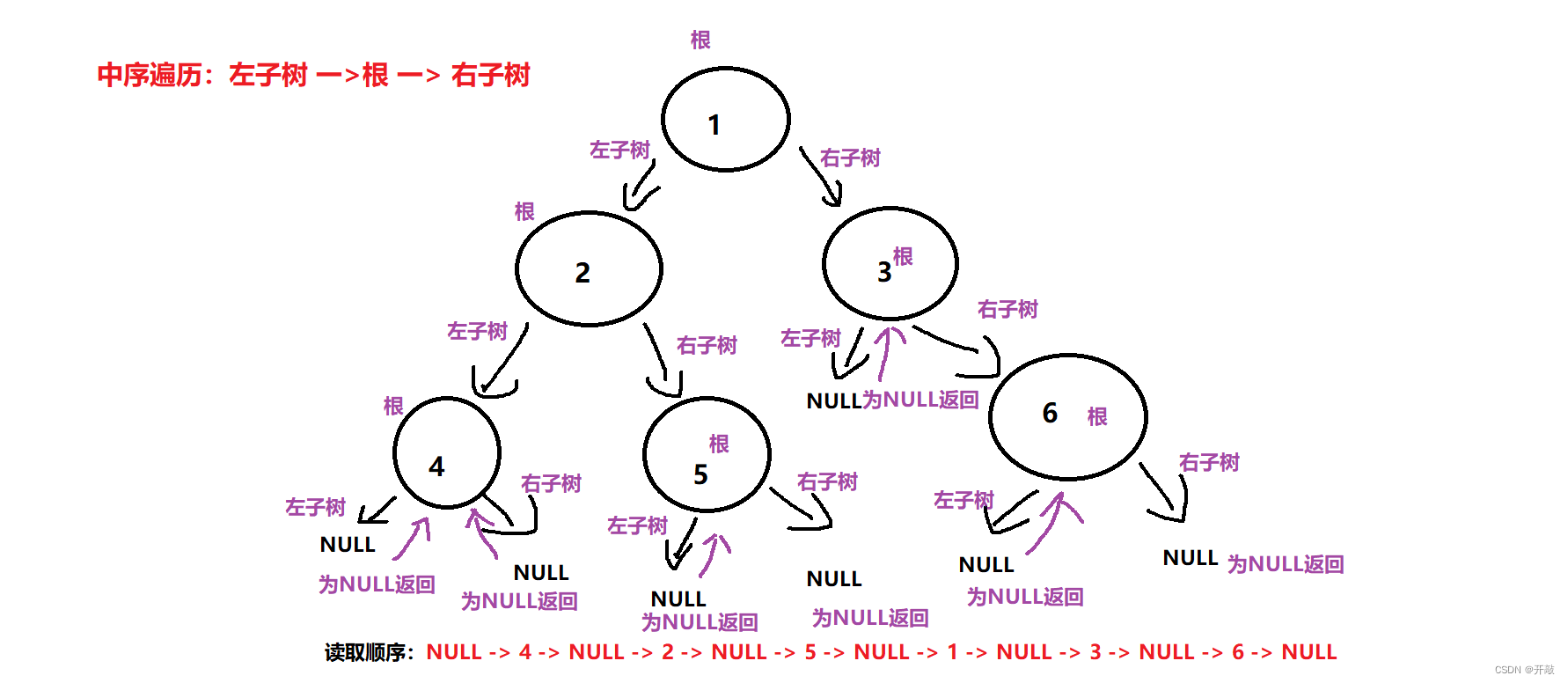
??② 中序:對于每個結點,都滿足 左子樹 一> 根 一> 右子樹 的遍歷順序
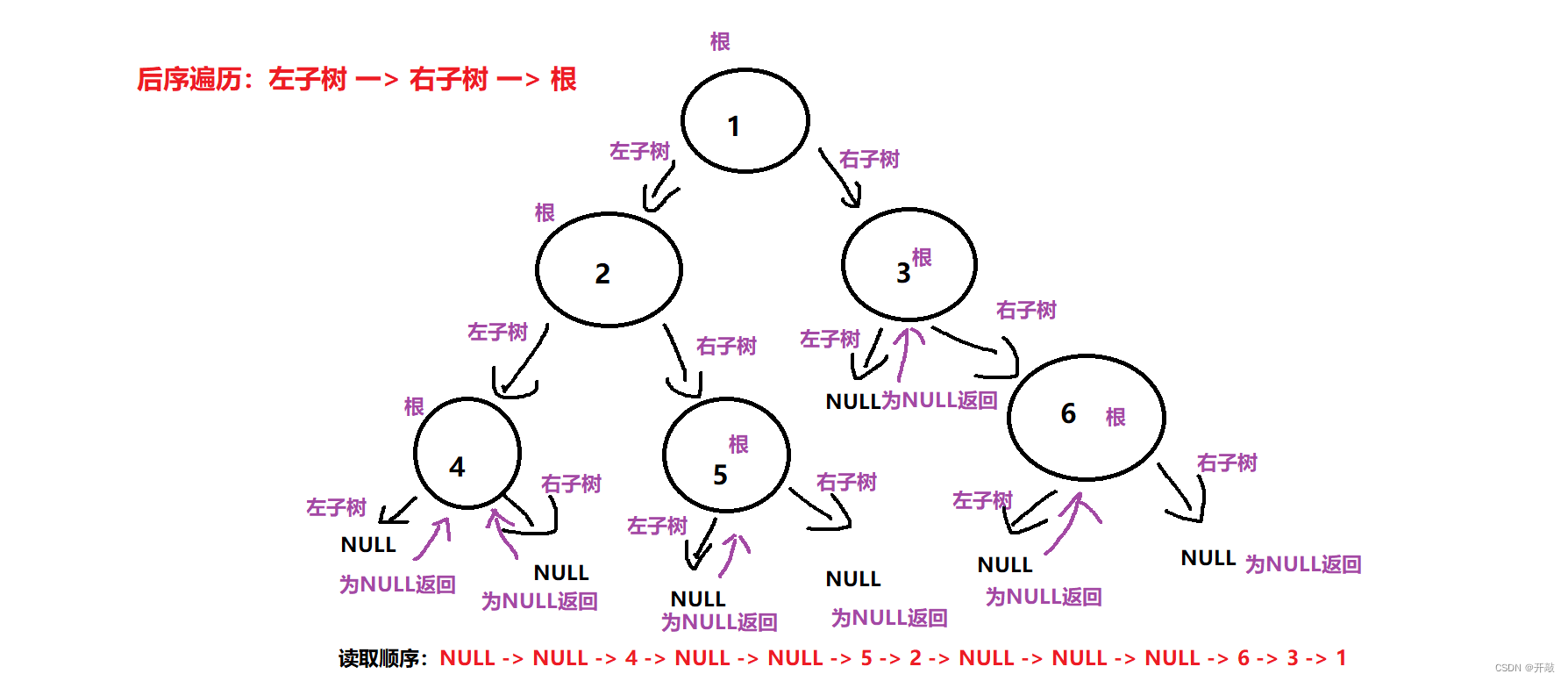
??③ 后序:對于每個結點,都滿足 左子樹 一> 右子樹 一> 根 的遍歷順序
??由于被訪問的結點必是某子樹的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解釋為根、根的左子樹和根的右子樹。NLR、LNR和LRN分別又稱為先根遍歷、中根遍歷和后根遍歷。
? 前序遍歷圖形解釋:

類似的可以推出中序遍歷:
以及后序遍歷:
? ? ? ? 4.2.2 層序遍歷
??層序遍歷:除了先序遍歷、中序遍歷、后序遍歷外,還可以對二叉樹進行層序遍歷。設二叉樹的根結點所在層數為1,層序遍歷就是從所在二叉樹的根結點出發,首先訪問第一層的樹根結點,然后從左到右訪問第2層上的結點,接著是第三層的結點,以此類推,自上而下,自左至右逐層訪問樹的結點的過程就是層序遍歷。
??
? ? 4.3 結點個數及高度等
//二叉樹結點個數
//求二叉樹結點個數,也就是將每個根節點左右子樹結點個數相加,再加上根結點自身。
int TreeNodeSize(BT* node)
{
?? ?if (node == NULL)
?? ?{
?? ??? ?return 0;
?? ?}
?? ?return 1 + TreeNodeSize(node->left) + TreeNodeSize(node->right);
}//二叉樹葉結點個數
int TreeLeafSize(BT* node)
{
?? ?if (node == NULL)
?? ?{
?? ??? ?return 0;
?? ?}
?? ?if (node->left == NULL && node->right == NULL)
?? ?{
?? ??? ?return 1;
?? ?}
?? ?return TreeLeafSize(node->left) + TreeLeafSize(node->right);
}//二叉樹第K層結點個數
int TreeKSize(BT* node,int k)
{
?? ?if (node == NULL)
?? ?{
?? ??? ?return 0;
?? ?}
?? ?else if (k == 0)
?? ?{
?? ??? ?return 1;
?? ?}
?? ?return TreeKSize(node->left,k-1) + TreeKSize(node->right,k-1);
}//查找值為x的結點
BT* FindX(BT* node, BTDataType x)
{
?? ?if (node == NULL)
?? ?{
?? ??? ?return NULL;
?? ?}
?? ?if (node->val == x)
?? ?{
?? ??? ?return node;
?? ?}
?? ?BT* ansleft = FindX(node->left, x);
?? ?if (ansleft)
?? ?{
?? ??? ?return ansleft;
?? ?}
?? ?return FindX(node->right,x);
}
? ? 4.4 二叉樹基礎OJ聯系
? ?965. 單值二叉樹 - 力扣(LeetCode)
? ?100. 相同的樹 - 力扣(LeetCode)
? 101. 對稱二叉樹 - 力扣(LeetCode)
? ?144. 二叉樹的前序遍歷 - 力扣(LeetCode)
? ?94. 二叉樹的中序遍歷 - 力扣(LeetCode)
? ?145. 二叉樹的后序遍歷 - 力扣(LeetCode)
? 572. 另一棵樹的子樹 - 力扣(LeetCode)
? ? 4.5 二叉樹的創建和銷毀
??二叉樹遍歷_牛客題霸_牛客網 (nowcoder.com)
??//前序遍歷創建二叉樹
BT* BinaryTreeCreate(BTDataType* a, int* n)
{
?? ?if (a[*n] == 0)
?? ?{
?? ??? ?(*n)++;
?? ??? ?return NULL;
?? ?}
?? ?BT* node = (BT*)malloc(sizeof(BT));
?? ?node->val = a[(*n)++];
?? ?node->left = BinaryTreeCreate(a, n);
?? ?node->right = BinaryTreeCreate(a, n);
?? ?return node;
}//二叉樹銷毀(后序遍歷)
void ReleaseBinaryTree(BT* node)
{
?? ?if (node == NULL)
?? ?{
?? ??? ?return;
?? ?}
?? ?ReleaseBinaryTree(node->left);
?? ?ReleaseBinaryTree(node->right);
?? ?free(node);
}//判斷二叉樹是否是完全二叉樹
bool IsFullBinaryTree(BT* node)
{
?? ??? ?QE q;
?? ?//初始化隊列
?? ?QueInit(&q);
?? ?//入列,隊列中的val存放指向結點的指針
?? ?if (node)
?? ??? ?QuePush(&q, node);?? ?while (!QueEmpty(&q))
?? ?{
?? ??? ?QDataType phead = QueGetHead(&q);
?? ??? ?QuePop(&q);
?? ??? ?if (phead == NULL)
?? ??? ?{
?? ??? ??? ?break;
?? ??? ?}?? ??? ?QuePush(&q, phead->left);
?? ??? ?QuePush(&q, phead->right);
?? ?}
?? ?while (!QueEmpty(&q))
?? ?{
?? ??? ?QDataType phead = QueGetHead(&q);
?? ??? ?if (phead)
?? ??? ?{
?? ??? ??? ?QueRelease(&q);
?? ??? ??? ?return false;
?? ??? ?}
?? ??? ?QuePop(&q);
?? ?}
?? ?QueRelease(&q);
?? ?return true;
}


)
)




)








概述)
