Yalmip使用教程(8)-常見報錯及調試方法

????????博客中所有內容均來源于自己學習過程中積累的經驗以及對yalmip官方文檔的翻譯：https://yalmip.github.io/tutorials/

????????這篇博客將詳細介紹使用yalmip工具箱編程過程中的常見錯誤和相應的解決辦法。

1.optimize的輸出參數

????????眾所周知，optimize是yalmip用來求解優化問題的函數，其使用格式為：

sol = optimize(Constraints,Objective,options)

????????optimize函數的返回值sol是一個包含六個字段的結構體：

>> solsol = 包含以下字段的 struct:yalmipversion: '20210331'matlabversion: '9.1.0.441655 (R2016b)'yalmiptime: 0.0851solvertime: 0.0439info: 'Successfully solved (GUROBI-GUROBI)'problem: 0

? ? ? ?其中，yalmipversion表示Yalmip工具箱的版本，matlabversion表示Matlab的版本，yalmiptime表示Yalmip的建模時間，solvertime表示求解器的求解時間，info表示返回的信息，problem為求解成功的標志，0表示求解成功，1表示求解失敗。

????????其中最重要的參數就是problem和info，可以顯示求解是否成功，以及可能遇到的問題。因此通常可以在optimize函數求解之后再加一部分代碼來展示是否求解成功和求解失敗的原因：

if sol.problem == 0disp('求解成功')
else disp('求解失敗，失敗原因為：')disp(sol.info)
end

????????以下的代碼是一個能求解成功的例子：

x = sdpvar(2,1);
Constraints = [x <= 3 , x(1) >= 2 , x(2) >= 1];
Objective = [1 3]*x;
ops = sdpsettings;
sol = optimize(Constraints , Objective , ops);
if sol.problem == 0disp('求解成功')
else disp('求解失敗，失敗原因為：')disp(sol.info)
end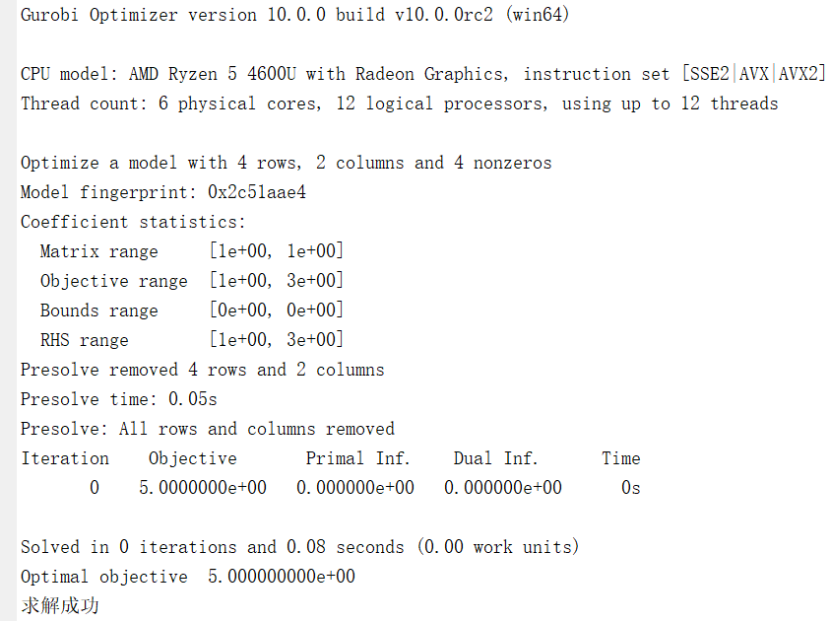

????????下面的例子是一個求解失敗的代碼：

x = sdpvar(2,1);
Constraints = [x <= 1 , x(1) >= 2 , x(2) >= 1];
Objective = [1 3]*x;
ops = sdpsettings;
sol = optimize(Constraints , Objective , ops);
if sol.problem == 0disp('求解成功')
else disp('求解失敗，失敗原因為：')disp(sol.info)
end

????????因為約束條件中x1≤1且x1≥2，所以導致優化問題無解。

????????在確保優化問題求解成功的情況下，可以采用value命令求出目標函數或者決策變量的取值，例如：

x = sdpvar(2,1);
Constraints = [x <= 3 , x(1) >= 2 , x(2) >= 1];
Objective = [1 3]*x;
ops = sdpsettings;
sol = optimize(Constraints , Objective , ops);
if sol.problem == 0disp('求解成功')x1 = value(x(1))x2 = value(x(2))Objective = value(Objective)
elsedisp('求解失敗，失敗原因為：')disp(sol.info)
end

????????結果為：

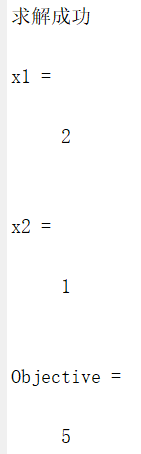
????????表示這個優化問題的最優解為x1=2，x2=1，目標函數最小值為5。

2.根據info信息判斷判斷解決方法

????????由第一節可知，yalmip工具箱中出現的大部分錯誤的原因都可以從optimize輸出參數的info屬性中查看。

????????例如，下面這個圖是非常常見的錯誤：

主要原因是優化問題無解，optimize函數求解失敗，后續又用到了優化問題中的一些變量，就會出現圖中的報錯。解決方法就是需要確保optimize函數可以求解成功。下面分別介紹一些常見的錯誤以及相應的解決方法。

2.1 solver not found

????????這個錯誤很簡單，就是字面意思（沒有安裝求解器），也是私信問我的朋友中最常見的錯誤。

????????解決這個報錯也很簡單，沒有求解器的去安裝一個，或者換成已經安裝過的求解器就行了。

????????和這個報錯同類型的提示還有：

Solver license cannot be located

Solver license expired

Specified solver name not recognized

License problems in solver

????????上述提示均可采用相同的方式解決。

2.2 Solver not applicable

????????從字面意思看，這個提示就是說求解器不適用。可能這么說大家還是不太明白。舉個例子，LINPROG是matlab自帶的線性規劃求解器，不具備求解二次規劃的功能，如果我們用這個求解器來解二次規劃問題，yalmip就會報錯提示求解器不可用，如下面的代碼：

clc
clearx1 = sdpvar(1);
x2 = sdpvar(1);
Constraints = [x1 >= 1 , x1 <= 2 , x2 <= 5 ,x2 >= 1];
Objective = x1^2 +9*x2;
ops = sdpsettings('solver' , 'LINPROG' , 'verbose' , 3 );
sol = optimize(Constraints , -Objective , ops);
sol.info

????????輸出結果為：

ans ='Solver not applicable (linprog does not support nonconvex quadratic terms in objective)'

????????如果我們在求解優化問題的過程中出現上面的提示，就需要確定優化問題的類型，仔細檢查你所使用的求解器是否支持該類型優化問題。換一個能求解該類型問題的求解器即可。

????????比如gurobi可以用來求解二次規劃問題，我們可以把上面例子中的求解器改為gurobi：

clc
clearx1 = sdpvar(1);
x2 = sdpvar(1);
Constraints = [x1 >= 1 , x1 <= 2 , x2 <= 5 ,x2 >= 1];
Objective = x1^2 +9*x2;
ops = sdpsettings('solver' , 'gurobi' , 'verbose' , 3 );
sol = optimize(Constraints , -Objective , ops);
sol.info

????????這時候就可以求解成功了：

ans ='Successfully solved (GUROBI-NONCONVEX)'

2.3 Unbounded objective function

????????從字面意思看，這個提示就是指優化模型的目標函數是無界的。具體來說，就是目標函數中存在沒有邊界范圍的變量，使得目標函數無法取得最大值（或最小值）。例如下面的優化問題：

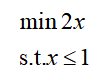
????????很明顯這是一個無界的優化問題，因為變量x沒有下界，因此無法找到2x的最小值，我們用yalmip求解試試：

clc
clearsdpvar x
Constraints = [x <= 1];
Objective = 2*x;
ops = sdpsettings('solver' , 'cplex' , 'verbose' , 3 );
sol = optimize(Constraints , Objective , ops);
sol.info

????????結果如下：

ans ='Unbounded objective function (CPLEX-IBM)'

????????針對目標函數無界的情況，調試的方法也很簡單。我們可以給定目標函數中涉及到的所有變量上下界，那么優化問題一般都可以從無解轉為有解，如果存在某些變量，無論上下界取何值，該變量的取值都處于我們給定的邊界上，那么就是因為這個變量沒有給定范圍，才導致目標函數無界。舉個例子：

clc
clearsdpvar x y zConstraints = [-1 <= [x y] <= 1, z <= 0];
Objective = x^2 + y + z;
ops = sdpsettings('solver' , 'cplex' , 'verbose' , 3 );
sol = optimize(Constraints , Objective , ops);
sol.info

????????這個優化問題也是無界，為了找到具體是哪個變量導致目標函數無界，我們可以按下面的步驟操作：

????????1）用allvariables函數取出目標函數中所有涉及的變量（注意，使用allvariables函數要求yalmip版本高于2021，舊版工具箱里面不存在該函數，舊版yalmip可以手動選取目標函數涉及的所有變量）：

UsedInObjective = allvariables(Objective);

????????如果使用了較低版本的yalmip，可以把代碼改成下面這樣：

UsedInObjective = [x, y, z];

????????2）人為給定這些變量的上下限：

Constraints = [Constraints, -100 <= UsedInObjective <= 100];

????????3）求解修改后的優化問題，并查看所有變量的取值：

ops = sdpsettings('solver' , 'cplex' , 'verbose' , 3 );
sol = optimize(Constraints , Objective , ops);
value([x y z])

????????結果如下：

ans =0    -1  -100

????????4）修改這些變量的上下限，并重復步驟2和3：

Constraints = [Constraints, -1000 <= UsedInObjective <= 1000];
ops = sdpsettings('solver' , 'cplex' , 'verbose' , 3 );
sol = optimize(Constraints , Objective , ops);
value([x y z])

????????結果如下：

ans =0    -1  -1000

我們可以看到，無論我們給定多大的邊界，變量z取值都位于邊界，因此就是未定義變量z的范圍或相關的約束，導致模型的目標函數無界，給定變量z的范圍或相關的約束即可解決該問題。

2.4 Infeasible problem

????????這個提示的字面意思是“不可行的問題”，也就是優化問題是無解的。一般情況下，優化問題無解都是因為約束條件之間存在矛盾或者限制的太死，我們需要通過調試找到問題所在。對于大規模的優化問題，調試的過程是很痛苦的，我們在調試之前可以先做一些簡單的檢查。

2.4.1 一些簡單檢查

????????1）檢查變量的定義是否存在問題，如0-1變量是否用binvar函數定義，連續變量是否用sdpvar函數定義，整數變量是否用intvar函數定義。

????????2）對于多維變量，檢查是否添加了’full’屬性。由于yalmip在定義N×N維變量時，如果不添加’full’屬性，將默認變量是對稱的，定義多維變量時很容易忽視這一點，導致模型不可行。

????????舉個例子，我在之前的博客中提到了一個數獨問題（Yalmip入門教程(3)-約束條件的定義-CSDN博客）：

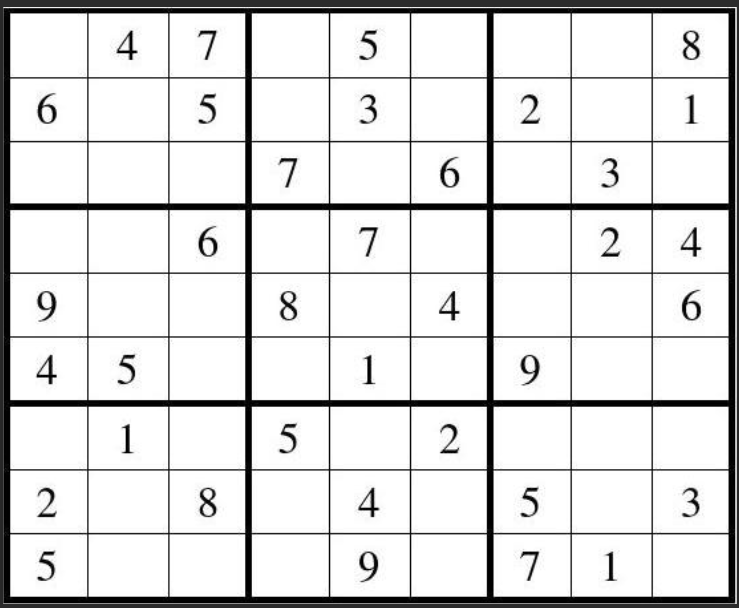
????????求解該問題的代碼如下：

clc
clearA0 = [
0 4 7 0 5 0 0 0 8;
6 0 5 0 3 0 2 0 1;
0 0 0 7 0 6 0 3 0;
0 0 6 0 7 0 0 2 4;
9 0 0 8 0 4 0 0 6;
4 5 0 0 1 0 9 0 0;
0 1 0 5 0 2 0 0 0;
2 0 8 0 4 0 5 0 3;
5 0 0 0 9 0 7 1 0;
];A = binvar(9,9,9,'full');
F = [sum(A,1) == 1, sum(A,2) == 1, sum(A,3) == 1];for i = 1:9for j = 1:9if A0(i,j)F = [F, A(i,j,A0(i,j)) == 1];endend
endfor m = 1:3for n = 1:3for k = 1:9s = sum(sum(A((m-1)*3+(1:3),(n-1)*3+(1:3),k)));             F = [F, s == 1];endend
enddiagnostics = optimize(F);Z = 0;
for i = 1:9Z = Z  + i*value(A(:,:,i));
end
Z

????????運行結果如下：

Z =3     4     7     2     5     1     6     9     86     8     5     4     3     9     2     7     11     2     9     7     8     6     4     3     58     3     6     9     7     5     1     2     49     7     1     8     2     4     3     5     64     5     2     6     1     3     9     8     77     1     3     5     6     2     8     4     92     9     8     1     4     7     5     6     35     6     4     3     9     8     7     1     2

????????如果我們將變量A定義時的’full’屬性刪除，再次運行的結果如下：

????????3）確定模型是否真的無解，而不是目標函數無界。有時候求解器會提示Either infeasible or unbounded，無法確定是優化問題無解還是目標函數無界。這時候我們可以將目標函數設為空，如果修改后可以求解成功，說明是目標函數無界，按照本博客2.3小節提到的方法進行調試即可。如果修改后還是提示模型不可行，那么就需要我們繼續調試。

2.4.2 調試較大規模的不可行問題

????????簡單來說，調試較大規模的不可行問題的思路就是依次向優化問題中添加約束條件，確定具體是哪組約束條件導致模型不可行或者哪些約束條件存在矛盾導致模型不可行。

????????我之前的博客給出了一個基于混合整數二階錐(MISOCP)的配電網重構代碼(基于混合整數二階錐(MISOCP)的配電網重構(附matlab代碼)-CSDN博客)，這是一個稍微有一丟丟復雜的優化問題，我悄咪咪地修改了其中一些參數，使得模型不可行，下面以修改后優化問題為例，講一下調試不可行問題的思路。

????????首先給出修改后的代碼：

%% 清除內存空間
clc
clear
close all
warning off
%% 系統參數
mpc = IEEE33;
nb=33;                              % 節點數
ns=1;                               % 電源節點數
nl=37;                              % 支路數
P_load=mpc.bus(:,3)/mpc.baseMVA;  % 有功負荷
Q_load=mpc.bus(:,4)/mpc.baseMVA;  % 無功負荷
r_ij=mpc.branch(:,3);              % 線路電阻
x_ij=mpc.branch(:,4);              % 線路電抗
M=1.06*1.06 - 0.94*0.94;
% 電源功率最大值
P_g_max=zeros(nb,1);
P_g_max(1)=10/mpc.baseMVA;
Q_g_max=zeros(nb,1);
Q_g_max(1)=10/mpc.baseMVA;
% 電源功率最小值
P_g_min=zeros(nb,1);
Q_g_min=[-10/mpc.baseMVA;zeros(nb-1,1)];
% 支路功率最大值
Sij_max=15/mpc.baseMVA;
% 最大電壓
Umax=[1;1.1*1.1*ones(32,1)];
Umin=[1;0.95*0.95*ones(32,1)];
% 流入節點的支路
branch_to_node=zeros(nb,nl);
% 流出節點的支路
branch_from_node=zeros(nb,nl);
for k=1:nlbranch_to_node(mpc.branch(k,2),k)=1;branch_from_node(mpc.branch(k,1),k)=1;
end%% 優化變量
z_ij=binvar(nl,1);% 支路開斷情況
U_i=sdpvar(nb,1);% 電壓的平方
L_ij=sdpvar(nl,1);% 電流的平方
P_ij=sdpvar(nl,1);% 線路有功功率
Q_ij=sdpvar(nl,1);% 線路無功功率
P_g=sdpvar(nb,1);% 電源有功出力
Q_g=sdpvar(nb,1);% 電源無功功率%% 約束條件
Constraints = [];
%% 1.潮流約束
m_ij=(1-z_ij)*M; 
Constraints = [Constraints, P_g-P_load+branch_to_node*P_ij-branch_to_node*(L_ij.*r_ij)-branch_from_node*P_ij == 0];
Constraints = [Constraints, Q_g-Q_load+branch_to_node*Q_ij-branch_to_node*(L_ij.*x_ij)-branch_from_node*Q_ij == 0];
Constraints = [Constraints,U_i(mpc.branch(:,1))-U_i(mpc.branch(:,2))<= m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*L_ij];
Constraints = [Constraints,U_i(mpc.branch(:,1))-U_i(mpc.branch(:,2))>= -m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*L_ij];
for k=1:nlConstraints = [Constraints, cone([2*P_ij(k) 2*Q_ij(k) L_ij(k)-U_i(mpc.branch(k,1))],L_ij(k)+U_i(mpc.branch(k,1)))];
end
Constraints = [Constraints, Sij_max'.^2.*z_ij >= P_ij.^2+Q_ij.^2];%% 2.拓撲約束
Constraints = [Constraints , sum(z_ij) == nb-ns];%% 3.注入功率約束
Constraints = [Constraints, P_g>=P_g_min,P_g<=P_g_max];
Constraints = [Constraints, Q_g>=Q_g_min,Q_g<=Q_g_max];%% 4.電壓上下限約束
Constraints = [Constraints, Umin <= U_i,U_i <= Umax];%% 目標函數
objective = sum(L_ij.*r_ij);%網損最小%% 設求解器
% gurobi求解器
ops=sdpsettings('verbose', 3, 'solver', 'gurobi','showprogress',1,'debug',1);
ops.gurobi.TimeLimit=600;                 % 運行時間限制為10min
ops.gurobi.MIPGap=0.01;                   % 收斂精度限制為0.01sol=optimize(Constraints,objective,ops);
value(objective)%% 分析錯誤標志
if sol.problem == 0disp('求解成功');
elsedisp('運行出錯');yalmiperror(sol.problem)
end

????????數據文件如下：

function mpc = IEEE33%% MATPOWER Case Format : Version 2
mpc.version = '2';%%-----  Power Flow Data  -----%%
%% system MVA base
mpc.baseMVA = 10;%% bus data
%   bus_i   type    Pd  Qd  Gs  Bs  area    Vm  Va  baseKV  zone    Vmax    Vmin
mpc.bus = [ %% (Pd and Qd are specified in kW & kVAr here, converted to MW & MVAr below)1   3   0   0   0   0   1   1   0   12.66   1   1   1;2   1   100 60  0   0   1   1   0   12.66   1   1.1 0.9;3   1   90  40  0   0   1   1   0   12.66   1   1.1 0.9;4   1   120 80  0   0   1   1   0   12.66   1   1.1 0.9;5   1   60  30  0   0   1   1   0   12.66   1   1.1 0.9;6   1   60  20  0   0   1   1   0   12.66   1   1.1 0.9;7   1   200 100 0   0   1   1   0   12.66   1   1.1 0.9;8   1   200 100 0   0   1   1   0   12.66   1   1.1 0.9;9   1   60  20  0   0   1   1   0   12.66   1   1.1 0.9;10  1   60  20  0   0   1   1   0   12.66   1   1.1 0.9;11  1   45  30  0   0   1   1   0   12.66   1   1.1 0.9;12  1   60  35  0   0   1   1   0   12.66   1   1.1 0.9;13  1   60  35  0   0   1   1   0   12.66   1   1.1 0.9;14  1   120 80  0   0   1   1   0   12.66   1   1.1 0.9;15  1   60  10  0   0   1   1   0   12.66   1   1.1 0.9;16  1   60  20  0   0   1   1   0   12.66   1   1.1 0.9;17  1   60  20  0   0   1   1   0   12.66   1   1.1 0.9;18  1   90  40  0   0   1   1   0   12.66   1   1.1 0.9;19  1   90  40  0   0   1   1   0   12.66   1   1.1 0.9;20  1   90  40  0   0   1   1   0   12.66   1   1.1 0.9;21  1   90  40  0   0   1   1   0   12.66   1   1.1 0.9;22  1   90  40  0   0   1   1   0   12.66   1   1.1 0.9;23  1   90  50  0   0   1   1   0   12.66   1   1.1 0.9;24  1   420 200 0   0   1   1   0   12.66   1   1.1 0.9;25  1   420 200 0   0   1   1   0   12.66   1   1.1 0.9;26  1   60  25  0   0   1   1   0   12.66   1   1.1 0.9;27  1   60  25  0   0   1   1   0   12.66   1   1.1 0.9;28  1   60  20  0   0   1   1   0   12.66   1   1.1 0.9;29  1   120 70  0   0   1   1   0   12.66   1   1.1 0.9;30  1   200 600 0   0   1   1   0   12.66   1   1.1 0.9;31  1   150 70  0   0   1   1   0   12.66   1   1.1 0.9;32  1   210 100 0   0   1   1   0   12.66   1   1.1 0.9;33  1   60  40  0   0   1   1   0   12.66   1   1.1 0.9;
];%% generator data
%   bus Pg  Qg  Qmax    Qmin    Vg  mBase   status  Pmax    Pmin    Pc1 Pc2 Qc1min  Qc1max  Qc2min  Qc2max  ramp_agc    ramp_10 ramp_30 ramp_q  apf
mpc.gen = [1   0   0   10  -10 1   100 1   10  0   0   0   0   0   0   0   0   0   0   0   0;
];%% branch data
%   fbus    tbus    r   x   b   rateA   rateB   rateC   ratio   angle   status  angmin  angmax
mpc.branch = [  %% (r and x specified in ohms here, converted to p.u. below)1   2   0.0922  0.0470  0   0   0   0   0   0   1   -360    360;2   3   0.4930  0.2511  0   0   0   0   0   0   1   -360    360;3   4   0.3660  0.1864  0   0   0   0   0   0   1   -360    360;4   5   0.3811  0.1941  0   0   0   0   0   0   1   -360    360;5   6   0.8190  0.7070  0   0   0   0   0   0   1   -360    360;6   7   0.1872  0.6188  0   0   0   0   0   0   1   -360    360;7   8   0.7114  0.2351  0   0   0   0   0   0   1   -360    360;8   9   1.0300  0.7400  0   0   0   0   0   0   1   -360    360;9   10  1.0440  0.7400  0   0   0   0   0   0   1   -360    360;10  11  0.1966  0.0650  0   0   0   0   0   0   1   -360    360;11  12  0.3744  0.1238  0   0   0   0   0   0   1   -360    360;12  13  1.4680  1.1550  0   0   0   0   0   0   1   -360    360;13  14  0.5416  0.7129  0   0   0   0   0   0   1   -360    360;14  15  0.5910  0.5260  0   0   0   0   0   0   1   -360    360;15  16  0.7463  0.5450  0   0   0   0   0   0   1   -360    360;16  17  1.2890  1.7210  0   0   0   0   0   0   1   -360    360;17  18  0.7320  0.5740  0   0   0   0   0   0   1   -360    360;2   19  0.1640  0.1565  0   0   0   0   0   0   1   -360    360;19  20  1.5042  1.3554  0   0   0   0   0   0   1   -360    360;20  21  0.4095  0.4784  0   0   0   0   0   0   1   -360    360;21  22  0.7089  0.9373  0   0   0   0   0   0   1   -360    360;3   23  0.4512  0.3083  0   0   0   0   0   0   1   -360    360;23  24  0.8980  0.7091  0   0   0   0   0   0   1   -360    360;24  25  0.8960  0.7011  0   0   0   0   0   0   1   -360    360;6   26  0.2030  0.1034  0   0   0   0   0   0   1   -360    360;26  27  0.2842  0.1447  0   0   0   0   0   0   1   -360    360;27  28  1.0590  0.9337  0   0   0   0   0   0   1   -360    360;28  29  0.8042  0.7006  0   0   0   0   0   0   1   -360    360;29  30  0.5075  0.2585  0   0   0   0   0   0   1   -360    360;30  31  0.9744  0.9630  0   0   0   0   0   0   1   -360    360;31  32  0.3105  0.3619  0   0   0   0   0   0   1   -360    360;32  33  0.3410  0.5302  0   0   0   0   0   0   1   -360    360;21  8   2.0000  2.0000  0   0   0   0   0   0   0   -360    360;9   15  2.0000  2.0000  0   0   0   0   0   0   0   -360    360;12  22  2.0000  2.0000  0   0   0   0   0   0   0   -360    360;18  33  0.5000  0.5000  0   0   0   0   0   0   0   -360    360;25  29  0.5000  0.5000  0   0   0   0   0   0   0   -360    360;
];%%-----  OPF Data  -----%%
%% generator cost data
%   1   startup shutdown    n   x1  y1  ... xn  yn
%   2   startup shutdown    n   c(n-1)  ... c0
mpc.gencost = [2   0   0   3   0   20  0;
];%% convert branch impedances from Ohms to p.u.
[PQ, PV, REF, NONE, BUS_I, BUS_TYPE, PD, QD, GS, BS, BUS_AREA, VM, ...VA, BASE_KV, ZONE, VMAX, VMIN, LAM_P, LAM_Q, MU_VMAX, MU_VMIN] = idx_bus;
[F_BUS, T_BUS, BR_R, BR_X, BR_B, RATE_A, RATE_B, RATE_C, ...TAP, SHIFT, BR_STATUS, PF, QF, PT, QT, MU_SF, MU_ST, ...ANGMIN, ANGMAX, MU_ANGMIN, MU_ANGMAX] = idx_brch;
Vbase = mpc.bus(1, BASE_KV) * 1e3;      %% in Volts
Sbase = mpc.baseMVA * 1e6;              %% in VA
mpc.branch(:, [BR_R BR_X]) = mpc.branch(:, [BR_R BR_X]) / (Vbase^2 / Sbase);%% convert loads from kW to MW
mpc.bus(:, [PD, QD]) = mpc.bus(:, [PD, QD]) / 1e3;

????????運行上面的代碼，得到的結果如下：

????????提示我們優化問題無解或者是目標函數無界。按照2.4.1小節第3點所提到的，我們先把目標函數設置為空，確定一下具體是優化問題無解還是目標函數無界：

sol=optimize(Constraints,[],ops);

????????得到的結果如下：

????????OK，現在確定了是優化問題不可行而不是目標函數無界，我們可以繼續調試。

????????1）首先只保留第一條約束，將其他約束都設為注釋，查看模型是否可行：

%% 清除內存空間
clc
clear
close all
warning off
%% 系統參數
mpc = IEEE33;
nb=33;                              % 節點數
ns=1;                               % 電源節點數
nl=37;                              % 支路數
P_load=mpc.bus(:,3)/mpc.baseMVA;  % 有功負荷
Q_load=mpc.bus(:,4)/mpc.baseMVA;  % 無功負荷
r_ij=mpc.branch(:,3);              % 線路電阻
x_ij=mpc.branch(:,4);              % 線路電抗
M=1.06*1.06 - 0.94*0.94;
% 電源功率最大值
P_g_max=zeros(nb,1);
P_g_max(1)=10/mpc.baseMVA;
Q_g_max=zeros(nb,1);
Q_g_max(1)=10/mpc.baseMVA;
% 電源功率最小值
P_g_min=zeros(nb,1);
Q_g_min=[-10/mpc.baseMVA;zeros(nb-1,1)];
% 支路功率最大值
Sij_max=15/mpc.baseMVA;
% 最大電壓
Umax=[1;1.1*1.1*ones(32,1)];
Umin=[1;0.95*0.95*ones(32,1)];
% 流入節點的支路
branch_to_node=zeros(nb,nl);
% 流出節點的支路
branch_from_node=zeros(nb,nl);
for k=1:nlbranch_to_node(mpc.branch(k,2),k)=1;branch_from_node(mpc.branch(k,1),k)=1;
end%% 優化變量
z_ij=binvar(nl,1);% 支路開斷情況
U_i=sdpvar(nb,1);% 電壓的平方
L_ij=sdpvar(nl,1);% 電流的平方
P_ij=sdpvar(nl,1);% 線路有功功率
Q_ij=sdpvar(nl,1);% 線路無功功率
P_g=sdpvar(nb,1);% 電源有功出力
Q_g=sdpvar(nb,1);% 電源無功功率%% 約束條件
Constraints = [];
%% 1.潮流約束
m_ij=(1-z_ij)*M; 
Constraints = [Constraints, P_g-P_load+branch_to_node*P_ij-branch_to_node*(L_ij.*r_ij)-branch_from_node*P_ij == 0];%% 目標函數
objective = sum(L_ij.*r_ij);%網損最小%% 設求解器
% gurobi求解器
ops=sdpsettings('verbose', 3, 'solver', 'gurobi','showprogress',1,'debug',1);
ops.gurobi.TimeLimit=600;                 % 運行時間限制為10min
ops.gurobi.MIPGap=0.01;                   % 收斂精度限制為0.01sol=optimize(Constraints, [], ops);
value(objective)%% 分析錯誤標志
if sol.problem == 0disp('求解成功');
elsedisp('運行出錯');yalmiperror(sol.problem)
end

????????運行結果如下：

????????這個結果，說明第一條約束沒問題，可以繼續添加約束。

????????2）只保留前2條約束，將其他約束都設為注釋，查看模型是否可行：

%% 清除內存空間
clc
clear
close all
warning off
%% 系統參數
mpc = IEEE33;
nb=33;                              % 節點數
ns=1;                               % 電源節點數
nl=37;                              % 支路數
P_load=mpc.bus(:,3)/mpc.baseMVA;  % 有功負荷
Q_load=mpc.bus(:,4)/mpc.baseMVA;  % 無功負荷
r_ij=mpc.branch(:,3);              % 線路電阻
x_ij=mpc.branch(:,4);              % 線路電抗
M=1.06*1.06 - 0.94*0.94;
% 電源功率最大值
P_g_max=zeros(nb,1);
P_g_max(1)=10/mpc.baseMVA;
Q_g_max=zeros(nb,1);
Q_g_max(1)=10/mpc.baseMVA;
% 電源功率最小值
P_g_min=zeros(nb,1);
Q_g_min=[-10/mpc.baseMVA;zeros(nb-1,1)];
% 支路功率最大值
Sij_max=15/mpc.baseMVA;
% 最大電壓
Umax=[1;1.1*1.1*ones(32,1)];
Umin=[1;0.95*0.95*ones(32,1)];
% 流入節點的支路
branch_to_node=zeros(nb,nl);
% 流出節點的支路
branch_from_node=zeros(nb,nl);
for k=1:nlbranch_to_node(mpc.branch(k,2),k)=1;branch_from_node(mpc.branch(k,1),k)=1;
end%% 優化變量
z_ij=binvar(nl,1);% 支路開斷情況
U_i=sdpvar(nb,1);% 電壓的平方
L_ij=sdpvar(nl,1);% 電流的平方
P_ij=sdpvar(nl,1);% 線路有功功率
Q_ij=sdpvar(nl,1);% 線路無功功率
P_g=sdpvar(nb,1);% 電源有功出力
Q_g=sdpvar(nb,1);% 電源無功功率%% 約束條件
Constraints = [];
%% 1.潮流約束
m_ij=(1-z_ij)*M; 
Constraints = [Constraints, P_g-P_load+branch_to_node*P_ij-branch_to_node*(L_ij.*r_ij)-branch_from_node*P_ij == 0];
Constraints = [Constraints, Q_g-Q_load+branch_to_node*Q_ij-branch_to_node*(L_ij.*x_ij)-branch_from_node*Q_ij == 0];%% 目標函數
objective = sum(L_ij.*r_ij);%網損最小%% 設求解器
% gurobi求解器
ops=sdpsettings('verbose', 3, 'solver', 'gurobi','showprogress',1,'debug',1);
ops.gurobi.TimeLimit=600;                 % 運行時間限制為10min
ops.gurobi.MIPGap=0.01;                   % 收斂精度限制為0.01sol=optimize(Constraints, [], ops);
value(objective)%% 分析錯誤標志
if sol.problem == 0disp('求解成功');
elsedisp('運行出錯');yalmiperror(sol.problem)
end

??????????運行結果如下：

????????這個結果，說明前2條約束沒問題且不存在矛盾，可以繼續添加約束。

????????……

????????3）一直重復上述步驟，可以發現直到加入最后一條電壓上下限約束之前，模型都是可行的，而加入電壓上下限約束之后模型就變得不可行了。說明問題很大可能就出現在這個電壓約束上。可能是電壓上下限設置的太緊，我們可以嘗試將節點電壓標幺值的下限從0.95改成0.9，再重新運行模型。

Umin=[1;0.9*0.9*ones(32,1)];

????????這時候發現可以求解出優化結果了：

????????我們可以再次把目標函數添加到優化問題中，模型依舊可行。

????????所以，這個優化問題不可行的原因就是電壓約束設置的太緊，稍微松弛一些即可。

????????對于其他不可行的優化問題，也可以按照相同的方式進行調試，找到存在問題的約束或互相矛盾的約束，再進行針對性的調整。

3.測試題

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/12910.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/12910.shtml
英文地址，請注明出處：http://en.pswp.cn/web/12910.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

5.7日學習記錄及相關問題解答

5.7日學習記錄及相關問題解答

1. 閱讀文章 復習 JAVA基礎——接口&#xff08;全網最詳細教程&#xff09; Java之對象的多態性&#xff08;使用生活中通俗的例子講解&#xff09; 新學 JavaWeb——Servlet&#xff08;全網最詳細教程包括Servlet源碼分析&#xff09; 有用 創建Dynamic Web Project工程&…
閱讀更多...
PS濾鏡插件Camera Raw 15.4升級，開啟智能修圖

PS濾鏡插件Camera Raw 15.4升級，開啟智能修圖

前段時間Adobe 更新了photoshop 的智能AI填充功能&#xff0c;深受很多設計師朋友的喜愛。Camera Raw作為PS的一個濾鏡插件對RAW圖片的處理上面有一定的優勢&#xff0c;Camera Raw 15.4升級了&#xff0c;開啟智能修圖木事&#xff0c;一起來看看吧&#xff01; Camera Raw濾鏡…
閱讀更多...
【2024華為HCIP831 | 高級網絡工程師之路】刷題日記（18）

【2024華為HCIP831 | 高級網絡工程師之路】刷題日記（18）

個人名片&#xff1a;&#x1faaa; &#x1f43c;作者簡介&#xff1a;一名大三在校生&#xff0c;喜歡AI編程&#x1f38b; &#x1f43b;???個人主頁&#x1f947;&#xff1a;落798. &#x1f43c;個人WeChat&#xff1a;hmmwx53 &#x1f54a;?系列專欄&#xff1a;&a…
閱讀更多...
ClassificationPrimitive 內部原理

ClassificationPrimitive 內部原理

ClassificationPrimitive 內部原理 發明 ClassificationPrimitive的真是個天才。其原理是利用 webgl 的模板緩沖區實現。 渲染兩次, 首先是繪制模板, 然后繪制真正的內容。 示意圖: function createClass() {const { program, uniforms } WebGLProgram.buildPrograms(gl, …
閱讀更多...
代碼隨想錄算法訓練營第36期DAY22

代碼隨想錄算法訓練營第36期DAY22

DAY22 654最大二叉樹 自己做的時候忽略了&#xff1a;nums.length>1的題給條件。所以每次遞歸都要判斷是否size()>1&#xff0c;不要空的。 /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *rig…
閱讀更多...
牛客網刷題 | BC84 牛牛學數列2

牛客網刷題 | BC84 牛牛學數列2

目前主要分為三個專欄&#xff0c;后續還會添加&#xff1a; 專欄如下&#xff1a; C語言刷題解析 C語言系列文章 我的成長經歷 感謝閱讀&#xff01; 初來乍到&#xff0c;如有錯誤請指出&#xff0c;感謝&#xff01; 描述 這次牛牛又換了個數…
閱讀更多...
sql中的exists和in的區別

sql中的exists和in的區別

在SQL中&#xff0c;EXISTS 和 IN 都用于子查詢&#xff0c;但它們的用法和目的有所不同。 ### EXISTS EXISTS 是一個邏輯運算符&#xff0c;用于檢查子查詢是否返回任何行。如果子查詢返回至少一行&#xff0c;那么 EXISTS 子句的結果為 TRUE&#xff1b;否則&#xff0c;結果…
閱讀更多...
一個用Kotlin編寫簡易的串行任務調度器

一個用Kotlin編寫簡易的串行任務調度器

引言 由于項目中有處理大量后臺任務并且串行執行的需求&#xff0c;特意寫了一個簡易的任務調度器&#xff0c;方便監控每個任務執行和異常情況&#xff0c;任務之間互不影響。正如上所述&#xff0c;Kotlin中的TaskScheduler類提供了一個強大的解決方案&#xff0c;用于使用S…
閱讀更多...
「AIGC」Python實現tokens算法

「AIGC」Python實現tokens算法

本文主要介紹通過python實現tokens統計，避免重復調用openai等官方api，開源節流。 一、設計思路 初始化tokenizer使用tokenizer將文本轉換為tokens計算token的數量二、業務場景 2.1 首次加載依賴 2.2 執行業務邏輯 三、核心代碼 from transformers import AutoTokenizer imp…
閱讀更多...
React: memo

React: memo

React.memo 允許你的組件在 props 沒有改變的情況下跳過重新渲染。 const MemoizedComponent memo(SomeComponent, arePropsEqual?)React 通常在其父組件重新渲染時重新渲染一個組件。你可以使用 memo 創建一個組件&#xff0c;當它的父組件重新渲染時&#xff0c;只要它的新…
閱讀更多...
centos7服務器采用局域網內筆記本代理上網

centos7服務器采用局域網內筆記本代理上網

一、背景 某臺服務器操作系統是centos 7&#xff0c;不能上網。我想在上面裝個ftp軟件&#xff1a;vsftpd。 二、思路 要安裝這個軟件&#xff0c;有2種方案 1&#xff09;設置該臺centos7可以上網 2&#xff09;離線安裝vsftpd 鑒于各種依賴&#xff0c;萬一因為依賴不全或…
閱讀更多...
《海峽科技與產業》是什么級別的期刊？是正規期刊嗎？能評職稱嗎？

《海峽科技與產業》是什么級別的期刊？是正規期刊嗎？能評職稱嗎？

問題解答 問&#xff1a;《海峽科技與產業》期刊是什么級別&#xff1f; 答&#xff1a;國家級 主管單位&#xff1a;中華人民共和國科學技術部 主辦單位&#xff1a;科技部海峽兩岸科學技術交流中心 問&#xff1a;《海峽科技與產業》影響因子&#xff1f; 答&#xff1a;…
閱讀更多...
相位；傅里葉變換和傅里葉級數是什么；歐拉公式是什么，和傅里葉關系；

相位；傅里葉變換和傅里葉級數是什么；歐拉公式是什么，和傅里葉關系；

目錄 相位 傅里葉變換公式使用舉例 實際案例 傅里葉變換和傅里葉級數是什么
閱讀更多...
隨筆：棋友們

隨筆：棋友們

我是在小學二年級學會中國象棋的&#xff0c;準確說&#xff0c;是學會象棋的下棋規則的&#xff0c;師傅是二舅。我最早的對手就是同學波仔。波仔比我略早學會象棋&#xff0c;總用連珠炮欺負我&#xff0c;開局幾步棋就把我將死。我不知道怎么破解。輪到我先走時&#xff0c;…
閱讀更多...
扭虧為盈的賽力斯，真正進入穩態了嗎？

扭虧為盈的賽力斯，真正進入穩態了嗎？

“72小時內大定破1萬臺”。5月15日&#xff0c;問界新M5開啟全國大規模交付&#xff0c;從當前取得的成績來看&#xff0c;賽力斯的“富貴”似乎還將延續。 其實&#xff0c;此前基于問界新M7等車型的爆火&#xff0c;賽力斯已經找到了創收軌道。財報顯示&#xff0c;2024年一…
閱讀更多...
alist網盤自動同步

alist網盤自動同步

alist網盤自動同步 alist可以設置目錄定時轉存到各個網盤&#xff0c;做到夸網盤&#xff0c;多備份的效果可以將自己掛載的alist 下的各個目錄相互間進行同步&#xff0c;原理是采用alist原始api調用執行同步原理1.匹配文件名稱是否相同,2.文件大小是否相同&#xff0c;相同會…
閱讀更多...
一文詳細解析Google編碼規范工具cpplint的下載安裝與使用

一文詳細解析Google編碼規范工具cpplint的下載安裝與使用

目錄 一、什么是cpplint 二、cpplint能實現的功能 三、cpplint的下載與使用 1、配置python環境 2、安裝cpplint 四、cpplint常用命令講解 1、常用命令查看 2、常用命令詳解 3、命令使用方式 五、 cpplint的實用技巧 1、集成cpplint 1.1、修改調用接口. 1.2、直接把…
閱讀更多...
數據結構（C）：樹的概念和二叉樹初見

數據結構（C）：樹的概念和二叉樹初見

目錄 &#x1f37a;0.前言 1.樹概念及結構 2.認識一棵樹 3.樹的表示 3.1樹在實際中的運用&#xff08;表示文件系統的目錄樹結構&#xff09; 4.二叉樹 4.1特殊的二叉樹 4.2二叉樹的性質 &#x1f48e;5.結束語 &#x1f37a;0.前言 言C之言&#xff0c;聊C之識&…
閱讀更多...
卷積模型的剪枝、蒸餾---蒸餾篇--NST特征蒸餾（以deeplabv3+為例）

卷積模型的剪枝、蒸餾---蒸餾篇--NST特征蒸餾（以deeplabv3+為例）

本文使用NST特征蒸餾實現deeplabv3+模型對剪枝后模型的蒸餾過程； 一、NST特征蒸餾簡介 下面是兩張疊加了熱力圖（heat map）的圖片，從圖中很容易看出這兩個神經元具有很強的選擇性：左圖的神經元對猴子的臉部非常敏感，右側的神經元對字符非常敏感。這種激活實際上意味著神經…
閱讀更多...
程序員績效管理-序言

程序員績效管理-序言

開辟一個新專欄專門討論程序員績效管理。作為軟件開發企業&#xff0c;公司的命脈掌握在程序員手中。程序員的績效管理是個超級難題。小張和老王專欄介紹了兩個典型的人員。但是這是兩個虛擬的極端人員&#xff0c;大部分開發人員沒有那么容易分辨。1個任務&#xff0c;應該1天…
閱讀更多...
最新文章

Copyright @ 2022~2023