目錄

🍺0.前言

1.樹概念及結構

2.認識一棵樹

?3.樹的表示

3.1樹在實際中的運用（表示文件系統的目錄樹結構）?

4.二叉樹?

4.1特殊的二叉樹?

4.2二叉樹的性質

💎5.結束語

---

🍺0.前言

? ? ? ? 言C之言，聊C之識，以C會友，共向遠方。各位博友的各位你們好啊，這里是持續分享數據結構知識的小趙同學，今天要分享的數據結構知識是樹的概念和二叉樹，在這一章，小趙將會向大家展開聊聊樹的概念和二叉樹。?

1.樹概念及結構

樹是一種非線性的數據結構，它是由n（n>=0）個有限結點組成一個具有層次關系的集合。把它叫做樹是因為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。

有一個特殊的結點，稱為根結點，根節點沒有前驅結點

除根節點外，其余結點被分成M(M>0)個互不相交的集合T1、T2、……、Tm，其中每一個集合Ti(1<= i <= m)又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，可以有0個或多個后繼

因此，樹是遞歸定義的。

這個定義其實看起來也是很耐看的，如果我們看這個去學習二叉樹，我感覺還是很有難度，那么下面小趙就用自己的語言來說一下什么叫樹。

先看一下現實中的樹：

我們現實中的樹往往是長成這樣，我們可以這樣想一下就是這個根就好像是我們的磁盤，然后每個樹根就好像是我們的文件夾，而每個文件里面又是不同的文件夾，這或許就是一個很好的樹的概念，這樣我們也能發現就是我們的樹的結構在我們的計算機中是極其常見的。?至于上面所說的根節點，遞歸實現等，小趙會在下面和大家一一聊到。

樹狀結構：

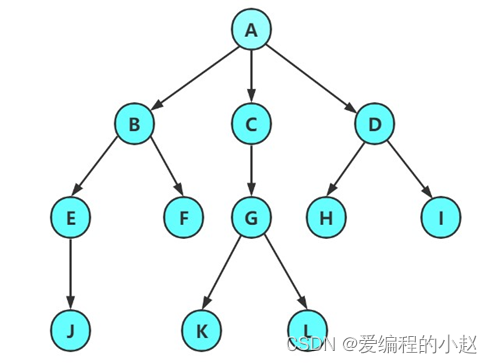
當然這里還有一個特別要注意的地方即：樹形結構中，子樹之間不能有交集，否則就不是樹形結構?。

2.認識一棵樹

其實認識一個全新的東西就好像是認識全新的物質，我們要知道他長什么樣子，他的每個部位叫什么，那么我們要想認識一棵樹也是一樣，那么下面我們就來感受一下這棵龐大的樹結構。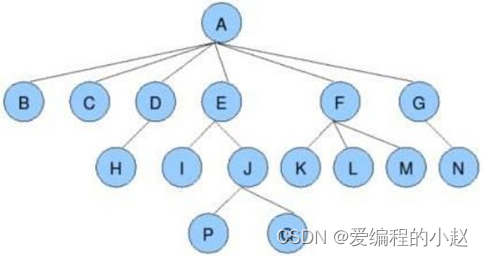

子樹：我們在樹結構里的命名是很像我們人類的家族一樣的，最上面一層的就好像是我們的祖先，那么子的意思其實就很像兒女的意思，那么對于A的兒女就是BCDEFG而不包含下面的那些HIJK等因為那些已經跨過了子了。

節點的度：一個節點含有的子樹的個數稱為該節點的度； 如上圖：A的為6

葉節點或終端節點（也就是這棵樹的最后）：度為0的節點稱為葉節點； 如上圖：B、C、H、I...等節點為葉節點

非終端節點或分支節點：度不為0的節點； 如上圖：D、E、F、G...等節點為分支節點

雙親節點或父節點：若一個節點含有子節點，則這個節點稱為其子節點的父節點； 如上圖：A是B的父節點

孩子節點或子節點：一個節點含有的子樹的根節點稱為該節點的子節點； 如上圖：B是A的孩子節點

兄弟節點：具有相同父節點的節點互稱為兄弟節點； 如上圖：B、C是兄弟節點

樹的度：一棵樹中，最大的節點的度稱為樹的度； 如上圖：樹的度為6

節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推

樹的高度或深度：樹中節點的最大層次； 如上圖：樹的高度為4（用家族的感覺就是這個家族有幾代人）

堂兄弟節點：雙親在同一層的節點互為堂兄弟；如上圖：H、I互為兄弟節點

節點的祖先：從根到該節點所經分支上的所有節點；如上圖：A是所有節點的祖先

子孫：以某節點為根的子樹中任一節點都稱為該節點的子孫。如上圖：所有節點都是A的子孫

森林：由m（m>0）棵互不相交的樹的集合稱為森林；

?3.樹的表示

樹結構相對線性表就比較復雜了，要存儲表示起來就比較麻煩了，既然保存值域，也要保存結點和結點之間 的關系，實際中樹有很多種表示方式如：雙親表示法，孩子表示法、孩子雙親表示法以及孩子兄弟表示法 等。我們這里就簡單的了解其中最常用的孩子兄弟表示法。

typedef int Datatype;
struct node
{struct node* leftchild;//左孩子（左子樹）struct node* rightchild;//右孩子（右子數）Datatype data;//當前節點存的數據
};

結構圖：?

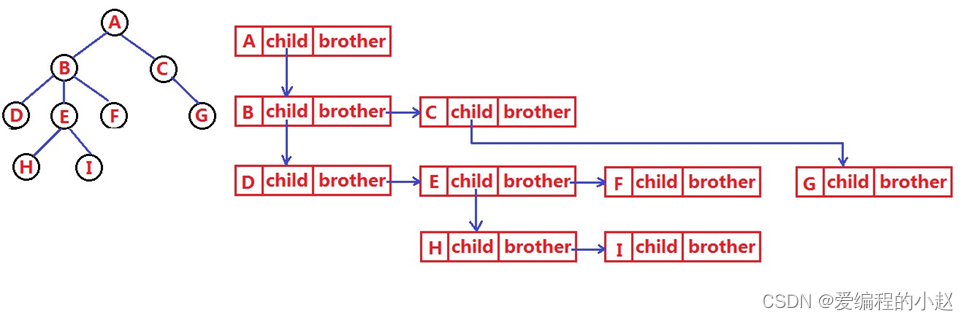
3.1樹在實際中的運用（表示文件系統的目錄樹結構）?

樹在我們計算機中的應用其實感覺和我們之前講過的文件夾差不多，這里小趙給的是我們的linux的樹狀目錄結構

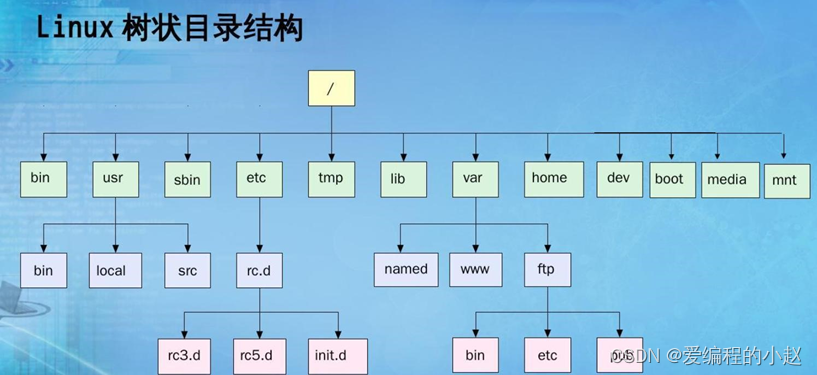
4.二叉樹?

我們在目前的學習中發現樹很大，很雜很多的支架，但我們今天是要學習肯定不是一個這么龐大的東西，因為太復雜了，也不好控制，所以我們今天要具體的去研究一個特殊的樹，這個樹就是二叉樹。是一種非常完美的樹，就像是我們的正方形一樣好看。

現實中二叉樹的樣子：

我們發現這樣的樹在現實生活還是非常少的，所以見到這樣的樹，我們程序員還是非常激動的，畢竟它占據了我們數據結構中非常重要的一部分。

二叉樹的概念：

一棵二叉樹是結點的一個有限集合，該集合:

1. 或者為空

2. 由一個根節點加上兩棵別稱為左子樹和右子樹的二叉樹組成

圖形：

從上圖可以看出：

1. 二叉樹不存在度大于2的結點

2. 二叉樹的子樹有左右之分，次序不能顛倒，因此二叉樹是有序樹?

注意：對于任意的二叉樹都是由以下幾種情況復合而成的：

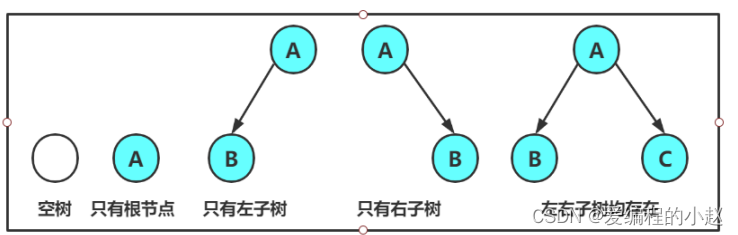
4.1特殊的二叉樹?

1.?滿二叉樹：一個二叉樹，如果每一個層的結點數都達到最大值，則這個二叉樹就是滿二叉樹。也就是 說，如果一個二叉樹的層數為K，且結點總數是 ，則它就是滿二叉樹。

說的更簡單一點就是滿了，沒有空的。除了葉節點其他都有兩個孩子。

2.完全二叉樹：完全二叉樹是效率很高的數據結構，完全二叉樹是由滿二叉樹而引出來的。對于深度為K 的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對 應時稱之為完全二叉樹。 要注意的是滿二叉樹是一種特殊的完全二叉樹。

看了這個其實我還是蠻暈的，但是換個說法可能就好理解一點，就是每棵樹首先一定只能有兩個子樹，那么就像是我們寫字一樣從左往右寫每一行，不能中間留空，中間留一個空擋就不是完全二叉樹，因為完全二叉樹對左右還是非常敏感的。

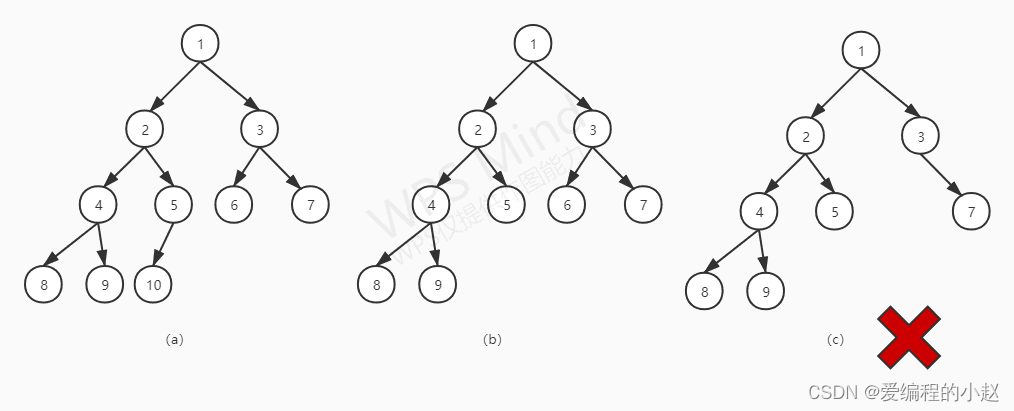
4.2二叉樹的性質

這里的絕大部分結論是我們可以用數學直接算出來的，這里小趙主要聊聊第三個結論。

首先是當我們只有一個根節點，然后我們開始給它一點一點節點：

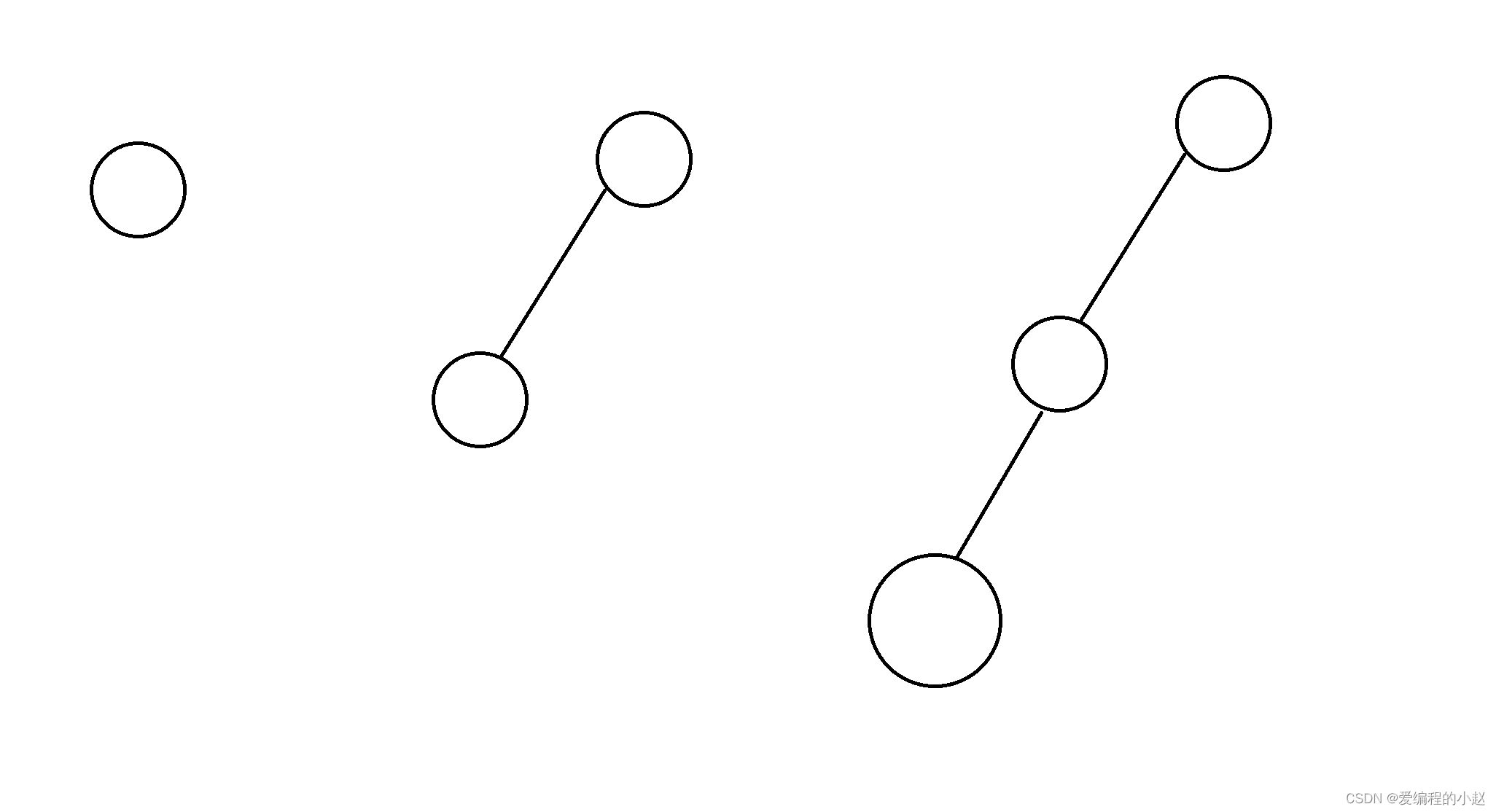
各位看這個圖的時候會發現，我們在增加度為1的節點的時候好像度為零的節點的個數始終沒有變過都是一個，可能我們會覺得好像沒什么關系，好我們接著往下。

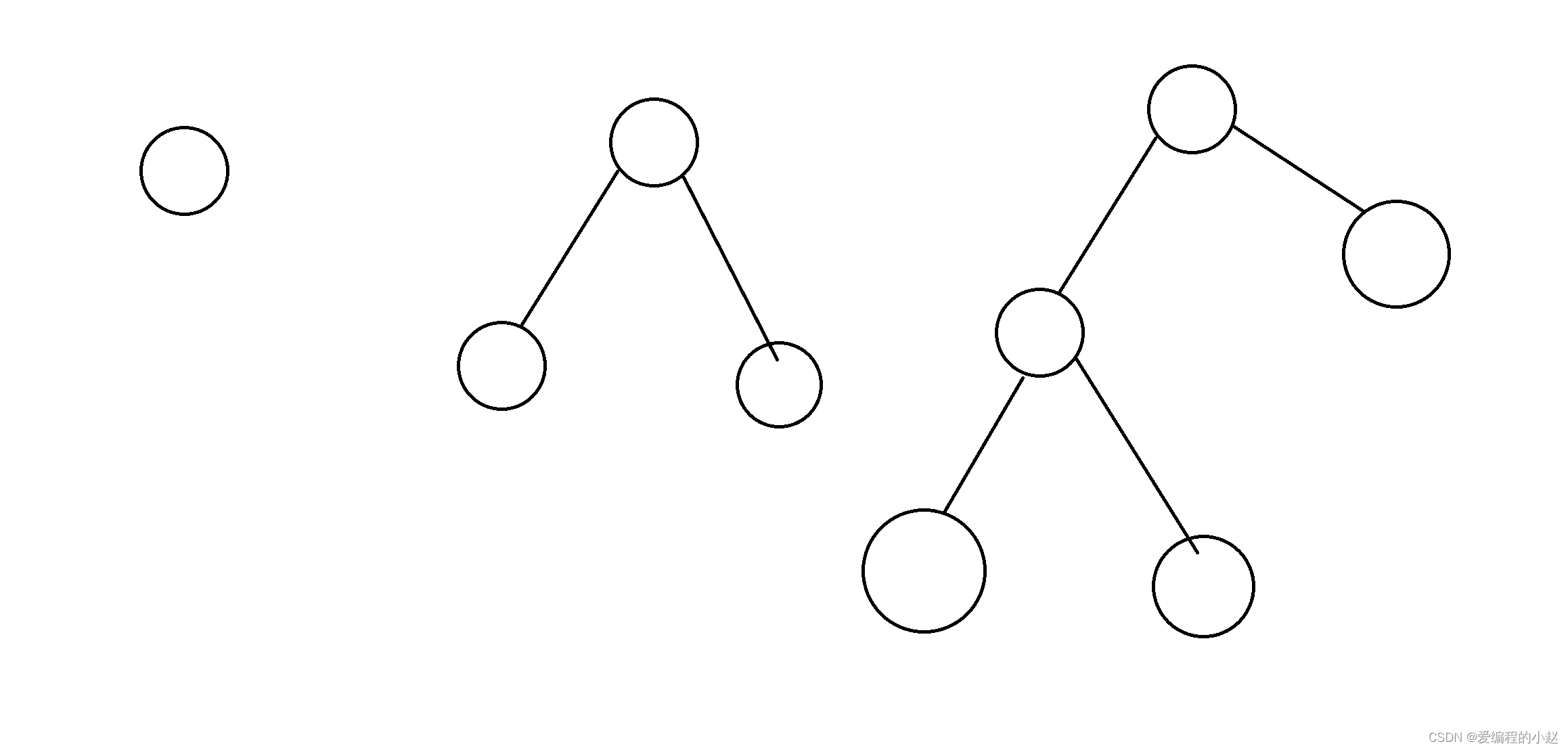
?這個時候我們把度為1的節點變為度為二的時候我們的發現每增加一個度為二就會增加一個度為零，所以結論就很明顯了。度為二的節點誕生一個，度為零的節點就增加一個，再加上原本的度為零的點，那么度為零的節點就等于度為二的節點的個數加一。

💎5.結束語

好了小趙今天的分享就到這里了，如果大家有什么不明白的地方可以在小趙的下方留言哦，同時如果小趙的博客中有什么地方不對也希望得到大家的指點，謝謝各位家人們的支持。你們的支持是小趙創作的動力，加油。

如果覺得文章對你有幫助的話，還請點贊，關注，收藏支持小趙，如有不足還請指點，小趙及時改正，感謝大家支持！！！