A Large Scale Synthetic Graph Dataset Generation Framework的學習筆記

文章的簡介

作者提出了一個可擴展的合成圖生成框架，能夠從真實圖中學習結構和特征分布，并生成任意規模的圖數據集，支持：

節點和邊的結構生成
節點和邊的特征生成
特征與結構的對齊（Aligner）

它區別于GraphWorld完全自定義參數生成具有各種統計屬性的“fake graph”，也不同于傳統的圖數據集OGB完全取之于真實世界。

文中涉及的一些公式，下面是我對它的理解

圖結構生成

目的與動機

目標是生成一個結構上與原始圖相似的圖結構（即鄰接矩陣）。
為了支持生成億萬邊規模的圖，采用了模型驅動的生成方法，而非深度學習式逐點生成。
核心方法是基于Stochastic Kronecker Graph (SKG) 的思想，是對 R-MAT 的一種泛化。

問題定義

輸入圖定義為：
$G = (S, F_V, F_E)$
其中

$S = (V, E)$ ：圖的結構（節點和邊）
$F_V$ ：節點特征矩陣
$F_E$ ：邊特征矩陣

目標是學習一個概率分布 $ρ(G)\rho(G)$ ，從中采樣生成新圖 $G^～pmodel(G)\hat G \sim p_{model}(G)$ 。

Kronecker圖生成機制 / R-MAT（Recursive MATrix）

使用一個基礎概率矩陣 $θs=[abcd],a+b+c+d=1\theta_s = \begin{bmatrix} a & b \\ c & d \end{bmatrix},a+b+c+d=1$ ，通過Kronecker乘法（克羅內克積）生成一個規模為 $n=2^m$ 個節點的隨機圖（通常為有向圖），邊數為 $E$ ，同時能產生真實網絡常見的“冪律度分布、社區/核心-邊緣結構”等特征。
支持生成非對稱、非方陣鄰接矩陣，適用于異構圖（如 K-partite 圖）。
對于 K-partite 圖，鄰接矩陣是一個塊矩陣，每個塊表示不同類型節點之間的連接。

其中最關鍵的是 $θs\theta_s$ 概率矩陣，它決定“每次二分遞歸時往哪一個象限走”的偏好。

節點編號與二進制

每個圖有 $n=2^m$ 個節點。給每一個節點一個m位二進制編號(0到 $2^m-1$ )。
一條邊 $(u, v)$ 對應到鄰接矩陣里的一格（第 $u$ 行第 $v$ 列）。R-MAT 會通過遞歸選擇象限的方式，逐步確定這格的位置，也就逐位確定 $u$ 和 $v$ 的二進制位。

生成一條邊：從開始到結束的 4 步

我們生成一條邊時，從整塊 $2m×2m2^m \times 2^m$ ，重復 $m$ 次“選象限”的動作

從整塊開始（還不知道源/目標的任何一位）。
一次遞歸劃分：把當前塊分成四個象限
- 左上（Top-Left, TL）概率 $a$
- 右上（TR）概率 $b$
- 左下（BL）概率 $c$
- 右下（BR）概率 $d$
落到某象限后，該象限就相當于“把源或目標的最高未確定那一位寫成 0/1”：
- 選到上半（TL 或 TR）：源端(行)這一位是 0；選到下半（BL 或 BR）：源端這一位是 1。
- 選到左半（TL 或 BL）：目標端（列）這一位是 0；選到右半（TR 或 BR）：目標端這一位是 1。
- 于是，這一次遞歸需要同時確定了 $u$ 的一位和 $v$ 的一位。
縮小到該象限，繼續做下一次遞歸（再次四分、再次按 $a, b, c, d$ 選擇），直到坐滿 $m$ 次。此時兩端的 $m$ 位都定了，得到了一個具體的 $(u, v)$ ，這樣就確立了一條邊。

一條邊的“落點”是 $m$ 次獨立象限選擇的產物。重復上面流程 $E$ 次，即可得到 $E$ 條邊。（可允許多重邊/自環，具體看實現是否去重或拒絕自環）。

和 3.2 節里推導 $c^kout\hat c_k^{out}$ 對齊

內部的二項分布概率質量函數

其實就是把“選象限”的四個概率合并成對行與列的邊際：

源端（行）選擇“上半/下半”的概率分別是
$Pr(源=上)=a+b\triangleq p, Pr(源=下)=c+d\triangleq 1- p.$
目標端（列）選擇“左半/右半”的概率分別是
$Pr(目標=左)=a+c\triangleq 1, Pr(目標=右)=b+d\triangleq 1- q.$
于是，在每一層遞歸：
源端這一位是 0（上半）的概率為 $p$ ，是 1（下半）的概率為 $1 ? p$ ；
目標端這一位是 0（左半）的概率為 $q$ ，是 1（右半）的概率為 $1 ? q$ 。

因為每層都是獨立同分布，這就帶來一個關鍵結論：
某個固定源節點 $u$ （它的二進制里有 $i$ 個 1）在一次“抽一條邊”里被選為源的單次概率是 $r_i=p^{m-i}(1-p)^i$
只與“1 的個數 i”有關，不依賴具體哪些位是 1。這樣“有 i 個 1 的節點”一共有 $(mi)\binom{m}{i}$ 個，而且它們的單次概率都相同——這正是 3.2 節里分層求和內部的二項分布的概率公式的來源。

一個具體的小例子（m=2）

設 $m = 2 ? n = 4$ 個節點，節點編號 00,01,10,11。
設 $a = 0.45, b = 0.15, c = 0.15, d = 0.25$ （滿足和為 1）。
- $p = a + b = 0.60 ； q = a + c = 0.60$ 。
生成一條邊需要 2 次象限選擇。比如兩次都抽到 TR（右上）：
- 第 1 次 TR：源位=0（上），目標位=1（右）；
- 第 2 次 TR：源位=0（上），目標位=1（右）；
- 得到 $(源節點 u = 00, 目標節點 v = 11)$ 。這條邊的路徑概率是 $b \times b$ 。

反過來想，假如給定了一個源節點（比如 $u = 10$ ，二進制有 $i = 1$ 個 1），則讓它作為一條邊的源的單次概率是 $r_1=p^{m-i}(1-p)^i=0.6^1 * 0.4^1=0.24$ 。

外部的二項分布概率質量函數

文中提到先生成與輸入圖等大小的圖（這里假設要生成的圖是無向節點異構邊同構圖），即生成鄰接矩陣 $A^\hat A$ 的大小是 $\times m$ ，生成圖 $G^\hat G$ 節點數量是 $n + m$ （因為異構這里 $n, m$ 分別表示兩種類型），而后在拓展。其中用一個二維概率分布矩陣 $θ\theta$ 來描述在生成圖中某個節點對之間存在邊的概率，即 $A^～θ\hat A \sim \theta$ 。
$θ=θS?min?(m,n)?θH?max?(0,n?m)?θV?max?(0,m?n)\theta = \theta_S^{\otimes \min(m,n)} \otimes \theta_H^{\otimes \max(0,n-m)} \otimes \theta_V^{\otimes \max(0,m-n)}$
這個矩陣不是直接給定的，而是通過多個 Kronecker 積構造出來的(參看上一節)，以便模擬真實圖的結構特性（如冪律分布、社區結構等）。其中：
$θS=[abcd],θH=[q1?q],θV=[p1?p]\theta_S = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, \quad \theta_H = \begin{bmatrix} q & 1 - q \end{bmatrix}, \quad \theta_V = \begin{bmatrix} p \\ 1 - p \end{bmatrix}$

$\lceil \log_2 M \rceil, \quad n = \lceil \log_2 N \rceil$
這里是因為R-MAT 是在一個 $2m(行數)×2n（列數）2^m(行數) \times 2^n（列數）$ 的鄰接矩陣上生成邊。R-MAT 的二分遞歸必須工作在 2 的冪次規模，但是現實中我們想要的節點數 $M, N$ 不一定正好是 2 的整數次冪。所以要取上整，保證覆蓋，然后再裁掉多余的。
$\quad q = a + c$
其中 $θH,θV\theta_H, \theta_V$ 分別表示用于擴展 Kronecker 種子矩陣 $θS\theta_S$ 的兩個邊緣矩陣，它們分別控制圖在橫向（列）和縱向（行）的擴展方式。它們的設計是為了生成非方形的鄰接矩陣，從而支持異構圖或 $K$ -部圖的生成。這里用于表示在 $n > m$ 時用 $θH\theta_H$ 拓展，相等時不拓展，否則用 $θV\theta_V$ 拓展。（KDD的發表版里公式表述有錯，請注意）。
為了仿照輸入圖的屬性， $θS\theta_S$ 的定義比較講究，定義了目標函數
$J(θS)∝∑kin=0kmaxin(ckin?c^kin)2+∑kout=0kmaxout(ckout?c^kout)2 J(\theta_S) \propto \sum_{k^{\text{in}}=0}^{k_{\text{max}}^{\text{in}}} \left( c_k^{\text{in}} - \hat{c}_k^{\text{in}} \right)^2 + \sum_{k^{\text{out}}=0}^{k_{\text{max}}^{\text{out}}} \left( c_k^{\text{out}} - \hat{c}_k^{\text{out}} \right)^2$
其中 $c_k^{in}$ 表示輸入圖 $G$ 中入度為 $k$ 的節點數量， $c^kin\hat c_k^{in}$ 則是估計的生成圖 $G^\hat G$ 中入度為 $k$ 的節點數量，同理可推別的。其中 $c^kout\hat c_k^{out}$ 定義為：
$c^kout=(Ek)∑i=0m(mi)[pm?i(1?p)i]k?[1?(pm?i(1?p)i)]E?k\hat{c}_k^{\text{out}} = \binom{E}{k} \sum_{i=0}^{m} \binom{m}{i} \left[ p^{m-i}(1-p)^i \right]^k \cdot \left[ 1 - \left( p^{m-i}(1-p)^i \right) \right]^{E-k}$
其外部也是一個二項分布概率質量函數，這里

把“抽一條邊、源端擊中某節點”看作一次伯努利試驗，成功概率取決于該節點所屬的“ $i$ 類”概率 $r_i$ 。
抽 E 條邊（獨立同分布）→ 該節點的出度 $Binomial(E,r_i)$ ；
則出度為 $k$ 的概率就是
$\binom{E}{k}r_i^k(1-r_i)^{E-k}$
每個 $i$ 類都有 $(mi)\binom{m}{i}$ 個節點，對所有的 $i$ 匯總，就得到“出度為 $k$ 的節點數的期望” $c^kout\hat c_k^{out}$

整個流程常見實現細節/變體

去重與自環：有的實現允許多重邊/自環（生成更快）；有的會在采樣后拒絕自環或去重，會稍增耗時。
- 多重邊 (multiple edges)：在抽 $E$ 條邊時，因為每條邊都是獨立隨機的，所以可能多次落在同一個位置 $(u, v)$ 。這就產生了相同的邊重復出現。
  比如節點 00 → 11 這條邊可能被抽中 5 次，那么結果圖里就有 5 條相同的邊。
- 自環 (self-loop)：邊的源端和目標端是同一個節點，即 $(u, u)$ 。
  比如 10 → 10，這種邊在很多場景下不是我們想要的。

(a) 允許多重邊/自環
做法：生成多少就記多少，不做過濾。
優點：實現簡單，速度最快（每次遞歸選象限 → 寫下結果 → 下一條）。
結果：圖可能會有重復邊，也可能有節點自己指向自己。
常見用途：做大規模隨機基準測試時（比如只關心度分布的大體形狀），允許多重邊/自環沒關系。
(b) 去重/去自環
去自環：如果生成的邊是 $(u, u)$ ，就丟棄，重新采樣。
去重：如果生成的邊在集合里已經有了，就丟棄，重新采樣。
優點：得到的圖是“簡單圖”（simple graph），即沒有重復邊和自環。很多圖算法理論默認輸入是簡單圖。
缺點：需要檢查和重采樣，帶來額外的開銷。尤其當E接近 $n^2$ （非常稠密）時，重復率會很高，代價可能很大。

噪聲/抖動：為避免棋盤狀偽影，常在每層對 $(a, b, c, d)$ 進行輕微擾動或隨機打亂節點標簽（label permutation）。

R-MAT每次遞歸選擇象限時都用同一個固定概率矩陣,重復 $m$ 次 → 節點編號和邊的分布跟二進制位高度相關。結果是：
1.節點的出度/入度不光依賴概率，還依賴它二進制編號的“模式”（多少個 1，多少個 0）。
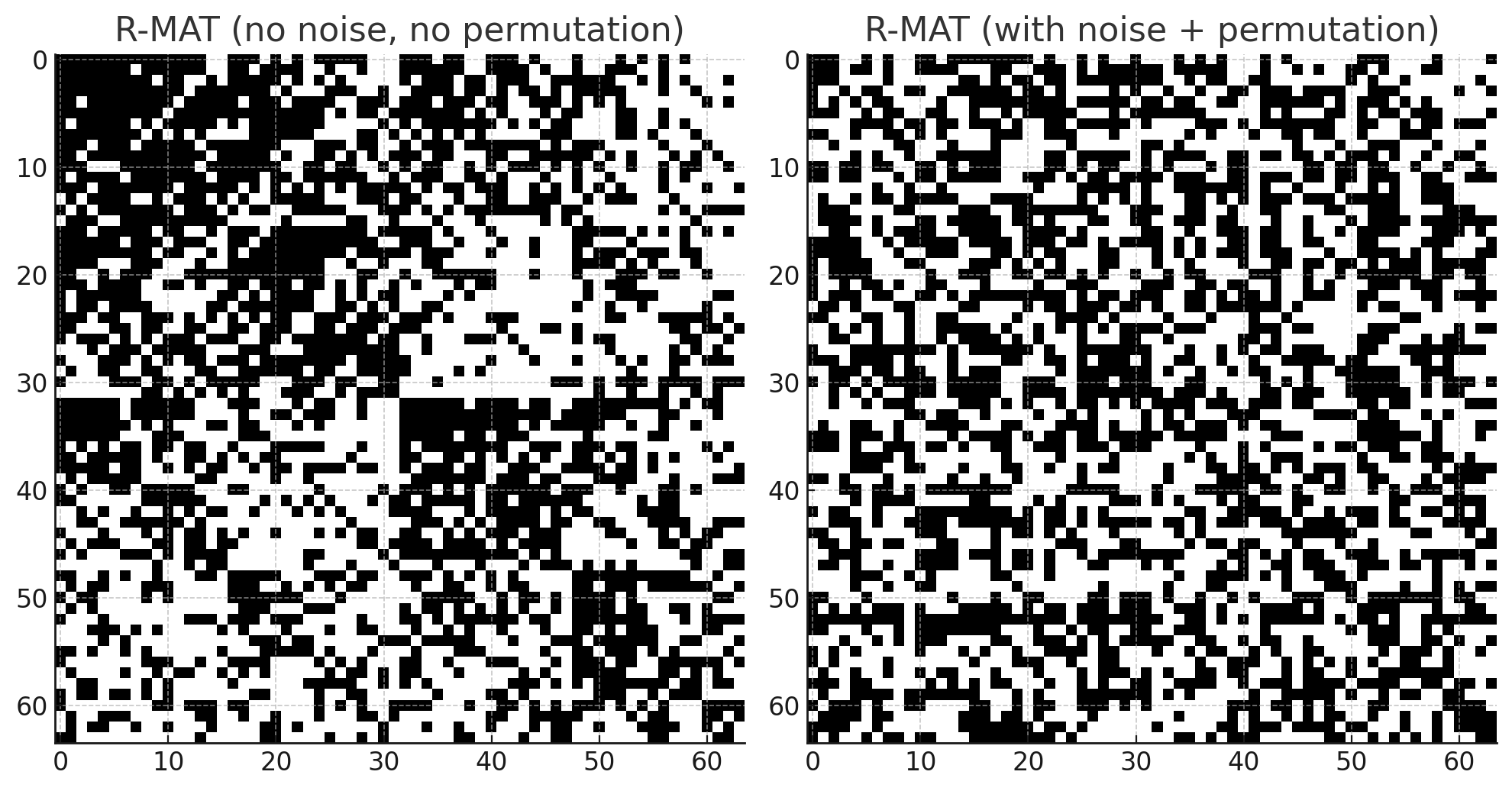
2.鄰接矩陣可視化時會出現一種棋盤格（checkerboard）樣的規律性偽影：某些大塊區域特別稠密，某些大塊特別稀疏，看起來像分層的棋盤格，而不是自然網絡里平滑的社區/局部密集結構。
這就是所謂的 R-MAT 偽影 (artifacts)。
為了緩解這種人為模式，人們引入隨機擾動：
(a) 概率擾動（noise / jitter）
在每一層遞歸時，不直接用固定的 $(a, b, c, d)$ ，而是加上一點小的隨機噪聲。例如 $a′=a+?a,b′=b+?b,c′=c+?c,d′=d+?d,a'=a+\epsilon_a, b'=b+\epsilon_b, c'=c+\epsilon_c, d'=d+\epsilon_d,$
然后再正規化保證它們加起來為 1。這樣，每一層遞歸的選擇概率都會有細微差別，避免邊總是嚴格落在固定模式的位置。
(b) 標簽隨機化（label permutation）
在生成邊之后，把節點的編號隨機打亂一次（或者在生成過程中，間歇性打亂節點標簽）。本質上就是“洗掉”二進制編號和度分布之間的強耦合關系，讓邊的分布更接近自然網絡。示意圖大概長這樣

無向圖：生成后把 $(u, v)$ 當作無向邊，或只保留 $u < v$ 的一半。
關系到 Kronecker/SKG：R-MAT 與后來的 Stochastic Kronecker Graph (SKG) 在思想上是對應的（一邊“遞歸抽象限”，一邊“Kronecker 乘生成矩陣”），參數可相互映射。