目錄
一、引言
二、梯度下降算法的原理
?三、梯度下降算法的實現
四、梯度下降算法的優缺點
優點：
缺點：
五、梯度下降算法的改進策略
1 隨機梯度下降（Stochastic Gradient Descent, SGD）
2 批量梯度下降（Batch Gradient Descent)
3 小批量梯度下降（Mini-batch Gradient Descent）
4 動量法（Momentum）
5 Adam算法
六、總結
一、引言
梯度下降算法是機器學習領域中最常用的優化算法之一。無論是線性回歸、邏輯回歸、神經網絡還是深度學習，我們都可以看到梯度下降的身影。它之所以如此受歡迎，是因為其原理簡單、易于實現，并且在許多情況下都能得到不錯的效果。本文將詳細介紹梯度下降算法的原理、實現方法、優缺點以及改進策略。
二、梯度下降算法的原理
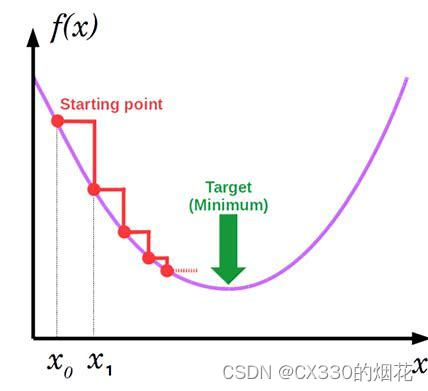
梯度下降算法的基本思想是利用目標函數的梯度信息來指導參數的更新，從而逐步逼近函數的最小值點。假設我們要優化的目標函數為f(x)，其中x是一個n維向量，表示模型的參數。我們的目標是找到x的最優值，使得f(x)取得最小值。
梯度下降算法的工作流程如下：
- 初始化參數x，可以隨機初始化或者根據經驗設置。
- 計算目標函數f(x)在當前位置x的梯度?f(x)。梯度是一個向量，表示函數在各個方向上的變化率。在梯度下降算法中，我們利用梯度的負方向（即-?f(x)）作為參數更新的方向。
- 按照一定的步長α（也稱為學習率）沿著梯度的負方向更新參數，即x = x - α?f(x)。步長α是一個超參數，需要根據實際情況進行調整。步長過大可能導致算法發散，步長過小則可能導致收斂速度過慢。
- 重復步驟2和3直到滿足停止條件（如達到預設的迭代次數、目標函數的值變化小于某個閾值等）。
?三、梯度下降算法的實現
梯度下降算法的實現相對簡單，下面是一個基本的Python實現示例：
import numpy as npdef gradient_descent(f, grad_f, x_start, alpha, num_iters):"""f: 目標函數grad_f: 目標函數的梯度函數x_start: 參數的初始值alpha: 學習率num_iters: 迭代次數"""x = x_startfor i in range(num_iters):grad = grad_f(x)x = x - alpha * gradreturn x
在這個示例中，我們假設目標函數f和它的梯度函數grad_f都是已知的。通過不斷迭代更新參數x，最終得到最優解。
四、梯度下降算法的優缺點
優點：
- 原理簡單，易于實現。在許多情況下都能得到不錯的效果。
- 可以應用于各種規模的數據集。
缺點：
- 對于非凸函數，可能陷入局部最優解而不是全局最優解。
- 收斂速度較慢，尤其是在處理大規模數據集時。
- 需要選擇合適的步長α，不同的步長可能導致不同的結果。
- 對于特征之間存在相關性的情況，梯度下降算法可能會變得非常慢。
五、梯度下降算法的改進策略
為了解決梯度下降算法存在的問題，人們提出了許多改進策略，下面介紹幾種常見的改進方法：
1 隨機梯度下降（Stochastic Gradient Descent, SGD）
SGD在每次迭代時只使用一個樣本來計算梯度并更新參數。這樣可以減少計算量并提高收斂速度，但也可能導致參數更新的方向不穩定。
2 批量梯度下降（Batch Gradient Descent)
批量梯度下降在每次迭代時使用所有樣本來計算梯度并更新參數。這種方法可以得到更準確的梯度估計但計算量較大。
3 小批量梯度下降（Mini-batch Gradient Descent）
小批量梯度下降是批量梯度下降和隨機梯度下降的一種折中方法。它每次迭代時使用一部分樣本來計算梯度并更新參數，既減少了計算量又保持了參數更新的穩定性。
4 動量法（Momentum）
動量法通過引入一個動量項來加速SGD的收斂速度。在每次迭代時，動量項會保留一部分上一次迭代的更新方向，并與當前梯度相結合來更新參數。這樣可以減少震蕩并加速收斂。
5 Adam算法
Adam算法是一種結合了Momentum和RMSProp的優化算法。它通過計算梯度的一階矩（平均值）和二階矩（未中心化的方差）來動態調整每個參數的學習率。Adam算法在許多情況下都能取得很好的效果，并且對于超參數的調整相對魯棒。
六、總結
梯度下降算法作為一種經典的優化算法，在機器學習和人工智能領域有著廣泛的應用。雖然它存在一些缺點，但通過不斷改進和優化，我們可以克服這些問題并提高算法的性能。
未來隨著深度學習和其他復雜模型的不斷發展，梯度下降算法及其改進策略將繼續發揮重要作用。
)
