*************************************優雅的分割線 **********************************

分享一波:程序員賺外快-必看的巔峰干貨

七、樹

7.1 樹

7.1.1 樹的定義

樹是我們計算機中非常重要的一種數據結構，同時使用樹這種數據結構，可以描述現實生活中的很多事物，例如族譜、單位的組織架構、等等。

樹是由n（n>=1）個有限結點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹

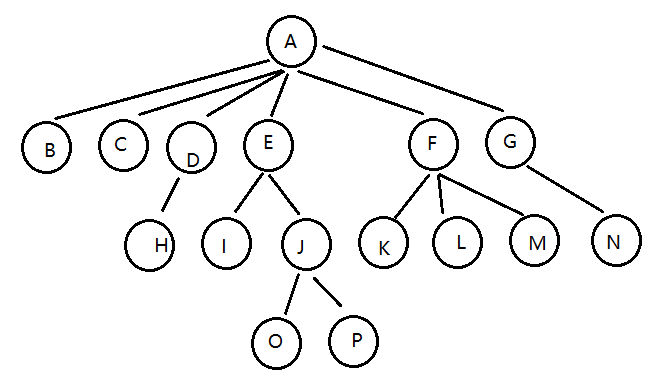
樹具有以下特點：

1. 每個結點有零個或多個子結點；
2. 沒有父結點的結點為根結點；
3. 每一個非根結點只有一個父結點；
4. 每個結點及其后代結點整體上可以看做是一棵樹，稱為當前結點的父結點的一個子樹；

7.1.2 樹的相關術語

結點的度：

一個結點含有的子樹的個數稱為該結點的度；

葉結點：

度為0的結點稱為葉結點，也可以叫做終端結點

分支結點：

度不為0的結點稱為分支結點，也可以叫做非終端結點

結點的層次：

從根結點開始，根結點的層次為1，根的直接后繼層次為2，以此類推

結點的層序編號：

將樹中的結點，按照從上層到下層，同層從左到右的次序排成一個線性序列，把他們編成連續的自然數。

樹的度：

樹中所有結點的度的最大值

樹的高度(深度)：

樹中結點的最大層次

森林：

m（m>=0）個互不相交的樹的集合，將一顆非空樹的根結點刪去，樹就變成一個森林；給森林增加一個統一的根 結點，森林就變成一棵樹

孩子結點：

一個結點的直接后繼結點稱為該結點的孩子結點

雙親結點(父結點)：

一個結點的直接前驅稱為該結點的雙親結點

兄弟結點：

同一雙親結點的孩子結點間互稱兄弟結點

7.2 二叉樹

7.2.1 二叉樹的基本定義

二叉樹就是度不超過2的樹(每個結點最多有兩個子結點)

滿二叉樹：

一個二叉樹，如果每一個層的結點數都達到最大值，則這個二叉樹就是滿二叉樹。

完全二叉樹：

葉節點只能出現在最下層和次下層，并且最下面一層的結點都集中在該層最左邊的若干位置的二叉樹

7.2.2 二叉查找樹

二叉查找樹是一種特殊的二叉樹，相對較小的值保存在左節點中，較大的值保存在右節點中。

根據對圖的觀察，我們發現二叉樹其實就是由一個一個的結點及其之間的關系組成的，按照面向對象的思想，我們 設計一個結點類來描述結點這個事物。

結點類API設計

類名	Node<Key,Value>
構造方法	Node(Key key, Value value, Node left, Node right)：創建Node對象
成員變量	1.public Node left:記錄左子結點 2.public Node right:記錄右子結點 3.public Key key:存儲鍵 4.public Value value:存儲值

二叉樹API設計

類名	BinaryTree<Key,Value>
構造方法	BinaryTree()：創建BinaryTree對象
成員變量	1.private Node root:記錄根結點 2.private int N:記錄樹中元素的個數
成員方法	1. public void put(Key key,Value value):向樹中插入一個鍵值對 2.private Node put(Node x, Key key, Value val)：給指定樹x上，添加鍵一個鍵值對，并返回添加后的新樹 3.public Value get(Key key):根據key，從樹中找出對應的值 4.private Value get(Node x, Key key):從指定的樹x中，找出key對應的值 5.public void delete(Key key):根據key，刪除樹中對應的鍵值對 6.private Node delete(Node x, Key key):刪除指定樹x上的鍵為key的鍵值對，并返回刪除后的新樹 7.public int size():獲取樹中元素的個數

7.2.3 代碼實現

插入方法put實現思想：

1. 如果當前樹中沒有任何一個結點，則直接把新結點當做根結點使用

2. 如果當前樹不為空，則從根結點開始：

   2.1 如果新結點的key小于當前結點的key，則繼續找當前結點的左子結點；

   2.2 如果新結點的key大于當前結點的key，則繼續找當前結點的右子結點；

   2.3 如果新結點的key等于當前結點的key，則樹中已經存在這樣的結點，替換該結點的value值即可。

查詢方法get實現思想：

從根節點開始：

1. 如果要查詢的key小于當前結點的key，則繼續找當前結點的左子結點；
2. 如果要查詢的key大于當前結點的key，則繼續找當前結點的右子結點；
3. 如果要查詢的key等于當前結點的key，則樹中返回當前結點的value。

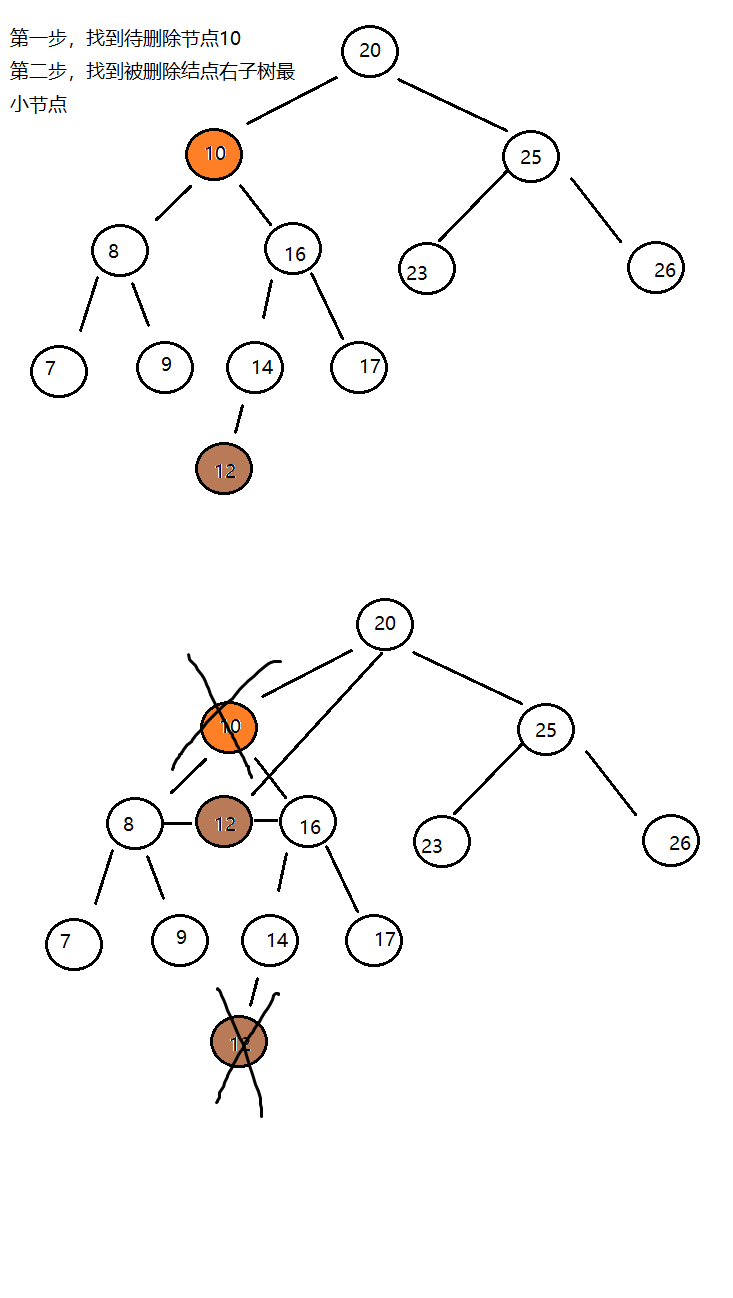
刪除方法delete實現思想：

1. 找到被刪除結點；
2. 找到被刪除結點右子樹中的最小結點minNode
3. 刪除右子樹中的最小結點
4. 讓被刪除結點的左子樹成為最小結點minNode的左子樹，讓被刪除結點的右子樹稱為最小結點minNode的右子樹
5. 讓被刪除結點的父節點指向最小結點minNode

package com.jg.tree;/*** 二叉樹** @Author: 楊德石* @Date: 2020/7/5 15:00* @Version 1.0*/
public class BinaryTree {/*** 記錄根結點*/private Node root;/*** 記錄樹中的元素個數*/private int n;public BinaryTree() {}/*** 向樹中插入一個鍵值對** @param key* @param value*/public void put(Integer key, String value) {root = put(root, key, value);}/*** 給指定的數x上，添加一個鍵值對，并返回添加后的新數** @param tree* @param key* @param value* @return*/private Node put(Node tree, Integer key, String value) {if (tree == null) {// 直接把新結點當成根結點使用// 個數+1n++;return new Node(null, null, key, value);}// 新結點的key大于當前結點的key，繼續找當前結點的右子結點if (key > tree.key) {tree.right = put(tree.right, key, value);} else if (key < tree.key) {// 新結點的key小于當前結點的key，繼續找當前結點的左子結點tree.left = put(tree.left, key, value);} else {// 新結點的key等于當前結點的keytree.value = value;}return tree;}/*** 從樹中找到對應的值** @param key* @return*/public String get(Integer key) {return get(root, key);}/*** 從指定的樹x中，找出key對應的值** @param tree* @param key* @return*/private String get(Node tree, Integer key) {if (tree == null) {return null;}// 如果要查詢的key大于當前節點的key。則繼續查找當前節點的右子結點if (key > tree.key) {return get(tree.right, key);} else if (key < tree.key) {// 如果要查詢的key小于當前節點的key。則繼續查找當前節點的左子結點return get(tree.left, key);} else {// 要查找的key和當前結點的key相等，返回valuereturn tree.value;}}/*** 根據key，刪除樹中對應的鍵值對** @param key*/public void delete(Integer key) {root = delete(root, key);}private Node delete(Node tree, Integer key) {if (tree == null) {return null;}// 待刪除的key大于當前節點的key，繼續找當前節點的右子結點if (key > tree.key) {tree.right = delete(tree.right, key);} else if (key < tree.key) {tree.left = delete(tree.left, key);} else {// 待刪除的key等于當前節點的key，說明當前結點就是要刪除的結點// 1. 如果當前結點的右子樹不存在，則直接返回當前結點的左子節點if (tree.right == null) {n--;return tree.left;}// 2. 如果當前結點的左子樹不存在，則直接返回當前結點的右子節點if (tree.left == null) {n--;return tree.right;}// 3. 當前結點的左右子樹都存在// 3.1 找到右子樹中最小的結點Node minNode = tree.right;// 二叉查找樹的左節點一定比右節點小，所以這里只需要遍歷左節點if (minNode.left != null) {minNode = minNode.left;}// 到這里，就找到了當前節點右子樹中最小的節點minNode// 3.2 刪除右子樹中最小的節點Node node = tree.right;while (node.left != null) {if (node.left.left == null) {// 說明n的左節點就是我們要找的最小結點node.left = null;} else {node = node.left;}}// 到這里，最小結點已經被刪除// 3.3 讓被刪除結點的左子樹成為最小結點的左子樹。讓被刪除結點的右子樹，成為最小結點的右子樹minNode.left = tree.left;minNode.right = tree.right;// 3.4 讓被刪除結點的父節點指向最小結點tree = minNode;// 個數-1n--;}return tree;}public int size() {return n;}private static class Node {public Node left;public Node right;public Integer key;public String value;public Node(Node left, Node right, Integer key, String value) {this.left = left;this.right = right;this.key = key;this.value = value;}}
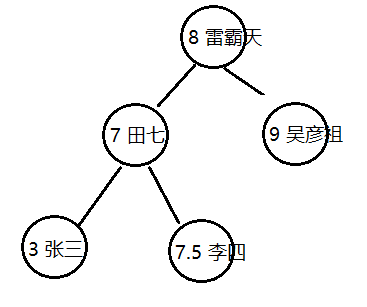
}class Test11 {public static void main(String[] args) {BinaryTree tree = new BinaryTree();tree.put(8, "雷霸天");tree.put(3, "張三");tree.put(7, "李四");tree.put(6, "田七");tree.put(9, "吳彥祖");System.out.println(tree.get(7));tree.delete(3);System.out.println(tree.size());}
}

7.2.4 二叉查找樹其他方法

查找二叉樹中最小的鍵

在某些情況下，我們需要查找出樹中存儲所有元素的鍵的最小值，比如我們的樹中存儲的是學生的排名和姓名數 據，那么需要查找出排名最低是多少名？這里我們設計如下兩個方法來完成：

方法	作用
public Key min()	找出樹中最小的鍵
private Node min(Node x)	找出指定樹X中，最小鍵所在的節點

查找二叉樹中最大的鍵

在某些情況下，我們需要查找出樹中存儲所有元素的鍵的最大值，比如比如我們的樹中存儲的是學生的成績和學生 的姓名，那么需要查找出最高的分數是多少？這里我們同樣設計兩個方法來完成：

方法	作用
public Key max()	找出樹中最大的鍵
public Node max(Node x)	找出指定樹中最大鍵所在的節點

7.2.5 二叉樹的基礎遍歷☆

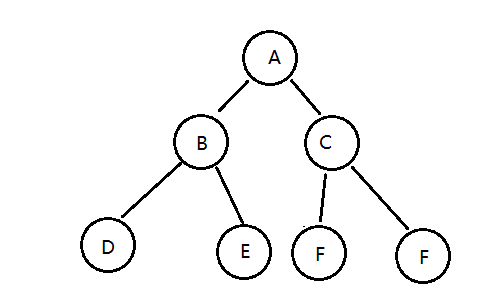
很多情況下，我們可能需要像遍歷數組數組一樣，遍歷樹，從而拿出樹中存儲的每一個元素，由于樹狀結構和線性 結構不一樣，它沒有辦法從頭開始依次向后遍歷，所以存在如何遍歷，也就是按照什么樣的搜索路徑進行遍歷的問 題。

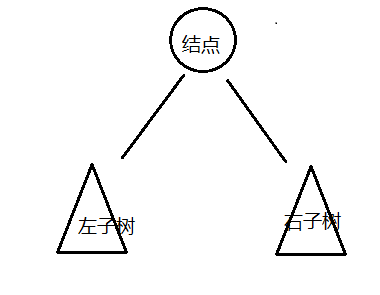
我們把樹簡單的畫作上圖中的樣子，由一個根節點、一個左子樹、一個右子樹組成，那么按照根節點什么時候被訪

問，我們可以把二叉樹的遍歷分為以下三種方式：

1. 前序遍歷； 先訪問根結點，然后再訪問左子樹，最后訪問右子樹
2. 中序遍歷； 先訪問左子樹，中間訪問根節點，最后訪問右子樹
3. 后序遍歷； 先訪問左子樹，再訪問右子樹，最后訪問根節點

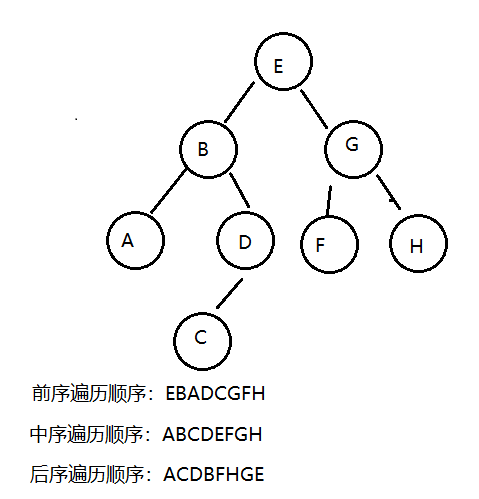
如果我們分別對下面的樹使用三種遍歷方式進行遍歷，得到的結果如下：

7.2.5.1 前序遍歷

遍歷API

方法	作用
public Queue preErgodic()	使用前序遍歷，獲取整個樹中的所有鍵
private void preErgodic(Node x,Queue keys)	使用前序遍歷，把指定樹x中的所有鍵放入到keys隊列中

實現過程中，我們通過前序遍歷，把每個結點的鍵取出，放入到隊列中返回即可。

實現步驟：

1. 把當前結點的key放入到隊列中;
2. 找到當前結點的左子樹，如果不為空，遞歸遍歷左子樹
3. 找到當前結點的右子樹，如果不為空，遞歸遍歷右子樹

    /*** 前序遍歷** @return*/public Queue preErgodic() {Queue keys = new Queue();preErgodic(root, keys);return keys;}private void preErgodic(Node tree, Queue keys) {if (tree == null) {return;}// 1.把當前結點的key放入到隊列中keys.enqueue(tree.key + "");// 2.找到當前節點的左子樹，如果不為空，遞歸遍歷左子樹if (tree.left != null) {preErgodic(tree.left, keys);}// 3.找到當前結點的右子樹，如果不為空，遞歸遍歷右子樹if (tree.right != null) {preErgodic(tree.right, keys);}}

7.2.5.2 中序遍歷

方法	作用
public Queue midErgodic()	使用中序遍歷，獲取整個樹中的所有鍵
private void midErgodic(Node x,Queue keys)	使用中序遍歷，把指定樹x中的所有鍵放入到keys隊列中

實現步驟：

1. 找到當前結點的左子樹，如果不為空，遞歸遍歷左子樹
2. 把當前結點的key放入到隊列中;
3. 找到當前結點的右子樹，如果不為空，遞歸遍歷右子樹

    /*** 中序遍歷** @return*/public Queue midErgodic() {Queue keys = new Queue();midErgodic(root, keys);return keys;}private void midErgodic(Node tree, Queue keys) {if (tree == null) {return;}// 1.找到當前結點的左子樹，如果不為空，遞歸遍歷左子樹if (tree.left != null) {midErgodic(tree.left, keys);}// 2.把當前結點的key放入到隊列中keys.enqueue(tree.key + "");// 3.找到當前結點的右子樹，如果不為空，遞歸遍歷右子樹if (tree.right != null) {midErgodic(tree.right, keys);}}

7.2.5.3 后序遍歷

方法	作用
public Queue afterErgodic()	使用后序遍歷，獲取整個樹中的所有鍵
private void afterErgodic(Node x,Queue keys)	使用后序遍歷，把指定樹x中的所有鍵放入到keys隊列中

實現步驟：

1. 找到當前結點的左子樹，如果不為空，遞歸遍歷左子樹
2. 找到當前結點的右子樹，如果不為空，遞歸遍歷右子樹
3. 把當前結點的key放入到隊列中;

代碼

    /*** 后序遍歷** @return*/public Queue afterErgodic() {Queue keys = new Queue();afterErgodic(root, keys);return keys;}private void afterErgodic(Node tree, Queue keys) {if (tree == null) {return;}// 1.找到當前結點的左子樹，如果不為空，遞歸遍歷左子樹if (tree.left != null) {afterErgodic(tree.left, keys);}// 2.找到當前結點的右子樹，如果不為空，遞歸遍歷右子樹if (tree.right != null) {afterErgodic(tree.right, keys);}// 3.把當前結點的key放入到隊列中keys.enqueue(tree.key + "");}

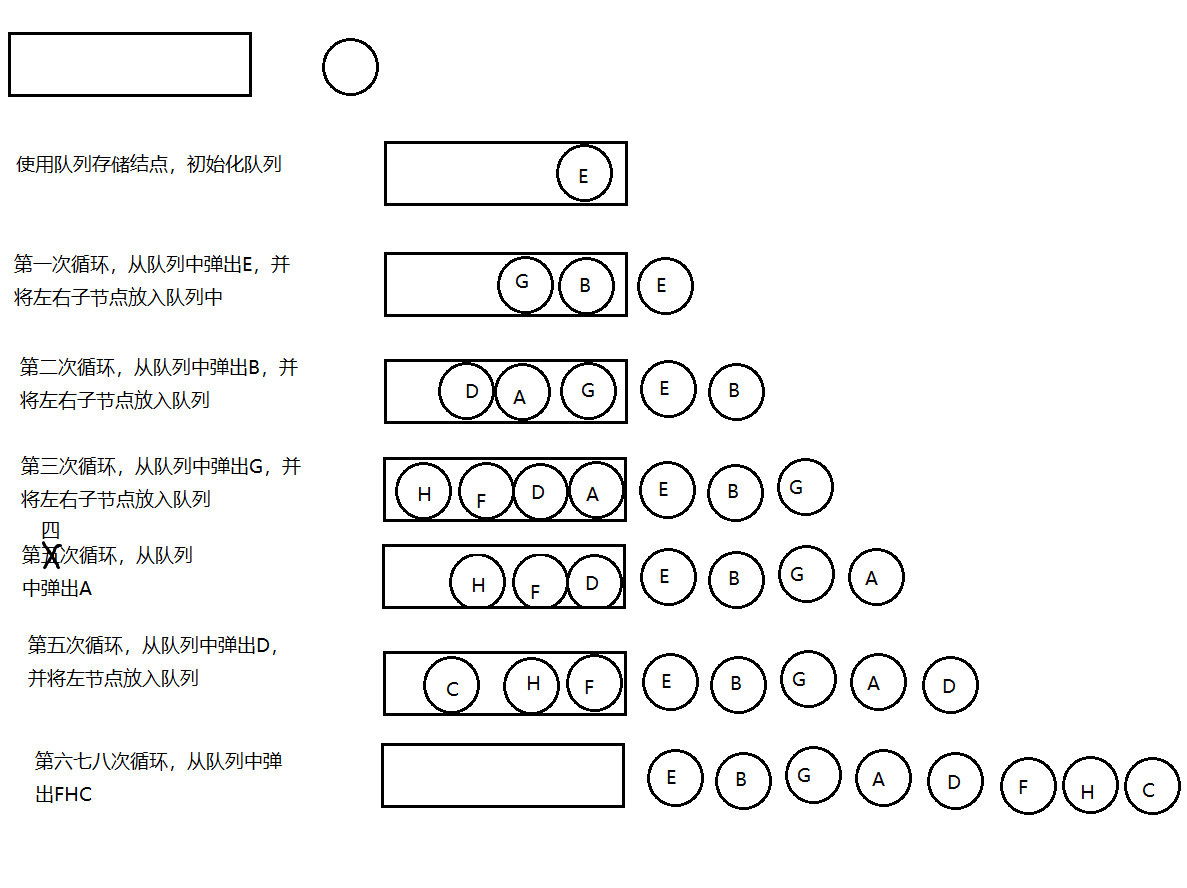
7.2.5.4 層序遍歷

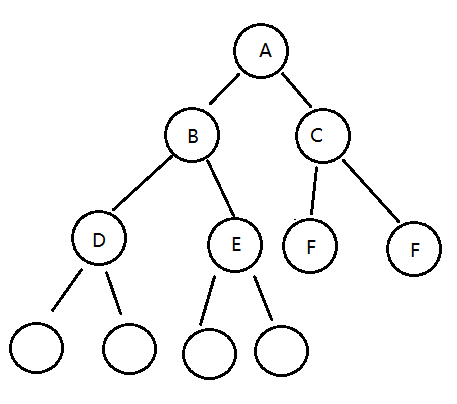
所謂的層序遍歷，就是從根節點（第一層）開始，依次向下，獲取每一層所有結點的值，有二叉樹如下：

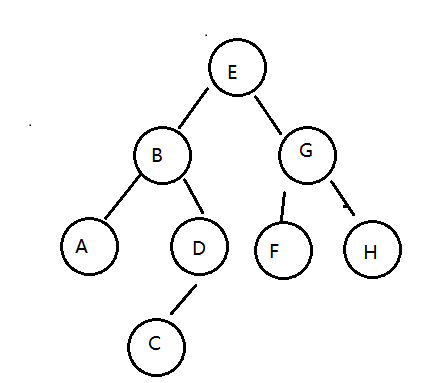
那么層序遍歷的結果是：EBGADFHC

API

方法	作用
public Queue layerErgodic()	使用層序遍歷，獲取整個樹中的所有鍵

實現步驟：

1. 創建隊列，存儲每一層的結點；

2. 使用循環從隊列中彈出一個結點：

   2.1獲取當前結點的key；

   2.2如果當前結點的左子結點不為空，則把左子結點放入到隊列中

   2.3如果當前結點的右子結點不為空，則把右子結點放入到隊列中

代碼

    /*** 層序遍歷** @return*/public Queue layerErgodic() {// 創建一個隊列，存儲每一層的節點ArrayQueue<Node> nodes = new ArrayQueue<>(n);// 創建一個隊列，用于存儲遍歷的節點Queue keys = new Queue();// 將當前節點存儲到nodes中nodes.add(root);// 遍歷queuewhile (!nodes.isEmpty()) {// 出列Node currentNode = nodes.remove(0);// 把節點的key存入到keys中keys.enqueue(currentNode.key + "");// 如果當前節點的左子節點不為空，則把左子節點放入到隊列中if (currentNode.left != null) {nodes.add(currentNode.left);}// 如果當前節點的右子節點不為空，把右子節點放到隊列中if (currentNode.right != null) {nodes.add(currentNode.right);}}return keys;}

非面向對象語言實現

    /*** 層序遍歷* 對于面向對象語言** @return*/public Queue layerErgodic() {// 創建一個隊列，存儲每一層的節點Queue nodes = new Queue();// 創建一個隊列，用于存儲遍歷的節點Queue keys = new Queue();// 將當前節點存儲到nodes中nodes.enqueue(root.key + "");// 遍歷queuewhile (!nodes.isEmpty()) {// 出列String key = nodes.dequeue();Node currentNode = getNode(root, Integer.parseInt(key));// 把節點的key存入到keys中keys.enqueue(currentNode.key + "");// 如果當前節點的左子節點不為空，則把左子節點放入到隊列中if (currentNode.left != null) {nodes.enqueue(currentNode.left.key + "");}// 如果當前節點的右子節點不為空，把右子節點放到隊列中if (currentNode.right != null) {nodes.enqueue(currentNode.right.key + "");}}return keys;}private Node getNode(Node tree, Integer key) {if (tree == null) {return null;}// 如果要查詢的key大于當前節點的key。則繼續查找當前節點的右子結點if (key > tree.key) {return getNode(tree.right, key);} else if (key < tree.key) {// 如果要查詢的key小于當前節點的key。則繼續查找當前節點的左子結點return getNode(tree.left, key);} else {// 要查找的key和當前結點的key相等，返回valuereturn tree;}}

7.2.5.5 最大深度問題 ☆

給定一棵樹，請計算樹的最大深度（樹的根節點到最遠葉子結點的最長路徑上的結點數）;如下面這棵樹的最大深度就是4

API設計

方法	作用
public int maxDepth()	計算整個樹的最大深度
private int maxDepth(Node x)	計算指定樹x的最大深度

實現步驟：

1. 如果根結點為空，則最大深度為0；
2. 計算左子樹的最大深度；
3. 計算右子樹的最大深度；
4. 當前樹的最大深度=左子樹的最大深度和右子樹的最大深度中的較大者+1

    /*** 計算最大深度** @return*/public int maxDepth() {return maxDepth(root);}private int maxDepth(Node tree) {if (tree == null) {return 0;}// 計算左右子樹的最大深度int max = 0;int leftMax = 0;int rightMax = 0;// 計算左子樹最大深度if (tree.left != null) {leftMax = maxDepth(tree.left);}// 計算右子樹最大深度if (tree.right != null) {rightMax = maxDepth(tree.right);}// 將二者較大的一方賦值給max。當前樹的最大深度就是max+1max = leftMax > rightMax ? leftMax + 1 : rightMax + 1;return max;}

7.2.6 折紙問題

需求：

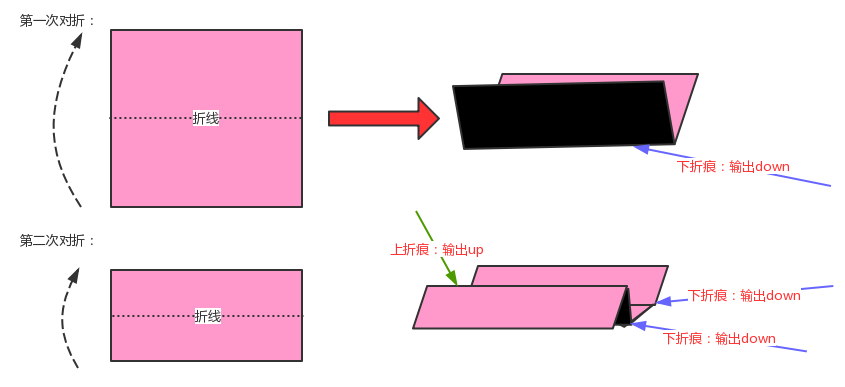
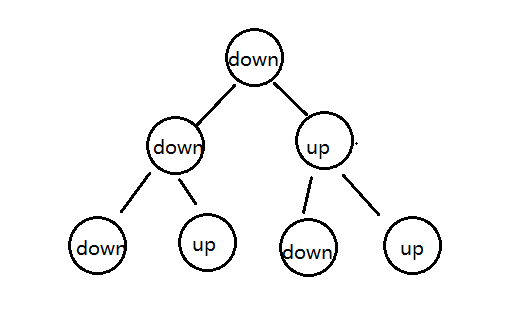
請把一段紙條豎著放在桌子上，然后從紙條的下邊向上方對折1次，壓出折痕后展開。此時 折痕是凹下去的，即折 痕突起的方向指向紙條的背面。如果從紙條的下邊向上方連續對折2 次，壓出折痕后展開，此時有三條折痕，從上 到下依次是下折痕、下折痕和上折痕。 給定一 個輸入參數N，代表紙條都從下邊向上方連續對折N次，請從上到下打印所有折痕的方向 例如：N=1時，打印： down；N=2時，打印： down down up

我們把對折后的紙張翻過來，讓粉色朝下，這時把第一次對折產生的折痕看做是根結點，那第二次對折產生的下折 痕就是該結點的左子結點，而第二次對折產生的上折痕就是該結點的右子結點，這樣我們就可以使用樹型數據結構 來描述對折后產生的折痕。

這棵樹有這樣的特點：

1. 根結點為下折痕；
2. 每一個結點的左子結點為下折痕；
3. 每一個結點的右子結點為上折痕；

實現步驟：

1. 定義結點類
2. 構建深度為N的折痕（樹結構）
3. 使用中序遍歷，打印出樹中所有結點的內容

構建深度為N的折痕樹：

1. 第一次對折，只有一條折痕，創建根節點
2. 如果不是第一次對折，判斷當前節點左右子樹是不是空
3. 如果是空，就給當前節點構建一個左子樹（down）和一個右子樹（up）
4. 獲取當前樹的左右子樹，重復第2步驟

代碼

public class PaperFold {public static void main(String[] args) {Node node = initTree(3);print(node);}/*** 使用中序遍歷打印出所有的節點* @param tree*/private static void print(Node tree) {if(tree == null) {return;}print(tree.left);System.out.print(tree.item+",");print(tree.right);}/*** 構建深度為N的折痕樹** @param n 需要構建的樹的深度*/private static Node initTree(int n) {// 根節點Node root = null;// 循環n次for (int i = 0; i < n; i++) {if (i == 0) {// 第一次對折，創建根節點root = new Node("down", null, null);} else {// 不是第一次// 創建一個隊列，將根節點存放到隊列中PaperQueue queue = new PaperQueue();// 根節點入列queue.enqueue(root);// 遍歷隊列while (!queue.isEmpty()) {// 從隊列中取出一個節點Node node = queue.dequeue();// 3. 獲取當前樹的左右子樹，重復第2步驟Node left = node.left;Node right = node.right;// 判斷左右子樹是否為空，如果不為空，存入隊列if (left != null) {queue.enqueue(left);}if (right != null) {queue.enqueue(right);}// 1. 如果不是第一次對折，判斷當前節點左右子樹是不是空if (node.left == null && node.right == null) {// 2. 如果是空，就給當前節點構建一個左子樹（down）和一個右子樹（up）node.left = new Node("down", null, null);node.right = new Node("up", null, null);}}}}return root;}// 定義結點類private static class Node {public String item;public Node left;public Node right;public Node(String item, Node left, Node right) {this.item = item;this.left = left;this.right = right;}}/*** 存放節點的隊列*/private static class PaperQueue {/*** 首結點*/private QueueNode head;/*** 當前隊列的元素個數*/private int n;/*** 記錄最后一個結點*/private QueueNode last;public PaperQueue() {head = new QueueNode(null, null);last = null;n = 0;}/*** 判斷隊列是否為空** @return*/public boolean isEmpty() {return n == 0;}/*** 從隊列中拿出一個元素** @return*/public Node dequeue() {if (isEmpty()) {return null;}// 不是空，出列// 獲取當前的第一個元素(對應圖中的1元素)QueueNode oldFirst = head.next;// 讓head結點指向下一個結點（對應圖中的2元素）head.next = head.next.next;// 個數-1n--;if (isEmpty()) {last = null;}return oldFirst.item;}/*** 往隊列中插入一個元素** @param t*/public void enqueue(Node t) {// 判斷last是否為nullif (last == null) {// last為空，要插入的元素就是lastlast = new QueueNode(t, null);// 讓首結點指向lasthead.next = last;} else {// 不是第一個元素// 取出舊結點（last）QueueNode oldLast = last;// 創建新的結點給lastlast = new QueueNode(t, null);// 讓舊的last元素指向新的結點oldLast.next = last;}// 個數+1n++;}private class QueueNode {public Node item;public QueueNode next;public QueueNode(Node item, QueueNode next) {this.item = item;this.next = next;}}}
}

7.3 堆

7.3.1 堆的定義

堆是計算機科學中一類特殊的數據結構的統稱，堆通常可以被看做是一棵完全二叉樹的數組對象。

堆的特性：

1. 它是完全二叉樹，除了樹的最后一層結點不需要是滿的，其它的每一層從左到右都是滿的，如果最后一層結點不是滿的，那么要求左滿右不滿。

   

2. 它通常用數組來實現。

具體方法就是將二叉樹的結點按照層級順序放入數組中，根結點在位置1，它的子結點在位置2和3，而子結點的子 結點則分別在位置4,5,6和7，以此類推。

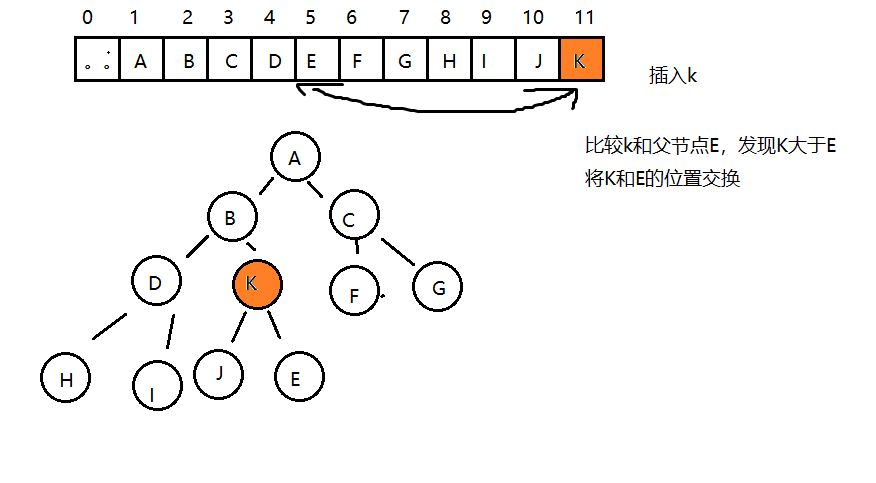
如果一個結點的位置為k，則它的父結點的位置為[k/2],而它的兩個子結點的位置則分別為2k和2k+1。這樣，在不 使用指針的情況下，我們也可以通過計算數組的索引在樹中上下移動：從a[k]向上一層，就令k等于k/2,向下一層就 令k等于2k或2k+1。

3. 每個結點都大于等于它的兩個子結點。這里要注意堆中僅僅規定了每個結點大于等于它的兩個子結點，但這兩個子結點的順序并沒有做規定，跟我們之前學習的二叉查找樹是有區別的。

API設計

類名	Heap
構造方法	Heap(int capacity)：創建容量為capacity的Heap對象
成員方法	1.private boolean less(int i,int j)：判斷堆中索引i處的元素是否小于索引j處的元素 2.private void exch(int i,int j):交換堆中i索引和j索引處的值 3.public T delMax():刪除堆中最大的元素,并返回這個最大元素 4.public void insert(T t)：往堆中插入一個元素 5.private void swim(int k):使用上浮算法，使索引k處的元素能在堆中處于一個正確的位置 6.private void sink(int k):使用下沉算法，使索引k處的元素能在堆中處于一個正確的位置
成員變量	1.private T[] imtes : 用來存儲元素的數組 2.private int N：記錄堆中元素的個數

7.3.2 代碼實現

7.3.2.1 insert方法實現

堆是用數組完成數據元素的存儲的，由于數組的底層是一串連續的內存地址，所以我們要往堆中插入數據，我們只 能往數組中從索引0處開始，依次往后存放數據，但是堆中對元素的順序是有要求的，每一個結點的數據要大于等 于它的兩個子結點的數據，所以每次插入一個元素，都會使得堆中的數據順序變亂，這個時候我們就需要通過一些 方法讓剛才插入的這個數據放入到合適的位置

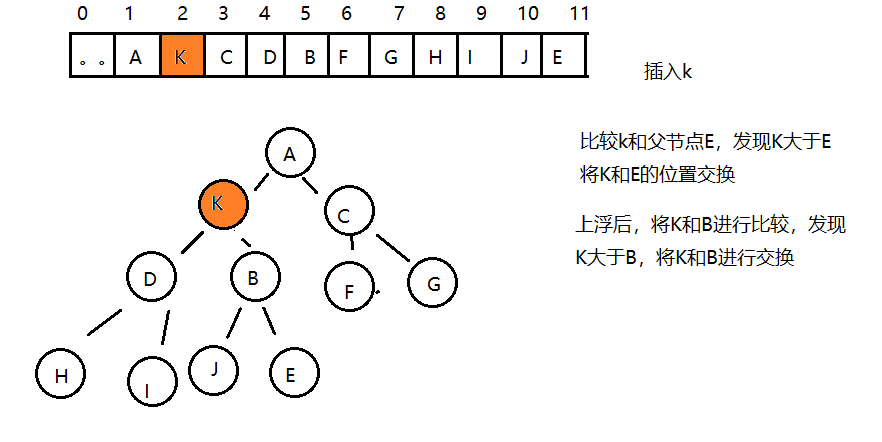
所以，如果往堆中新插入元素，我們只需要不斷的比較新結點a[k]和它的父結點a[k/2]的大小，然后根據結果完成 數據元素的交換，就可以完成堆的有序調整。

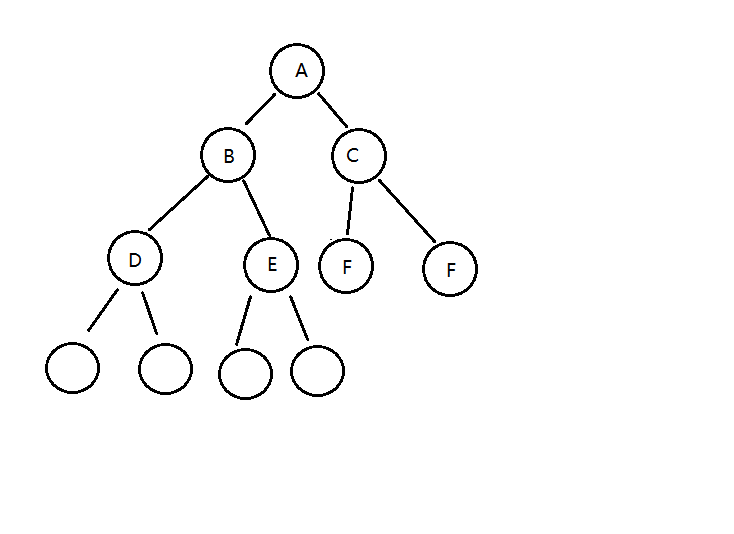
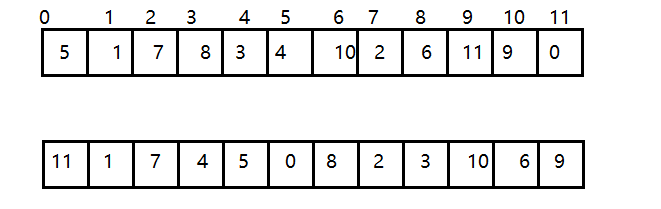
7.3.2.2 delMax刪除最大元素方法

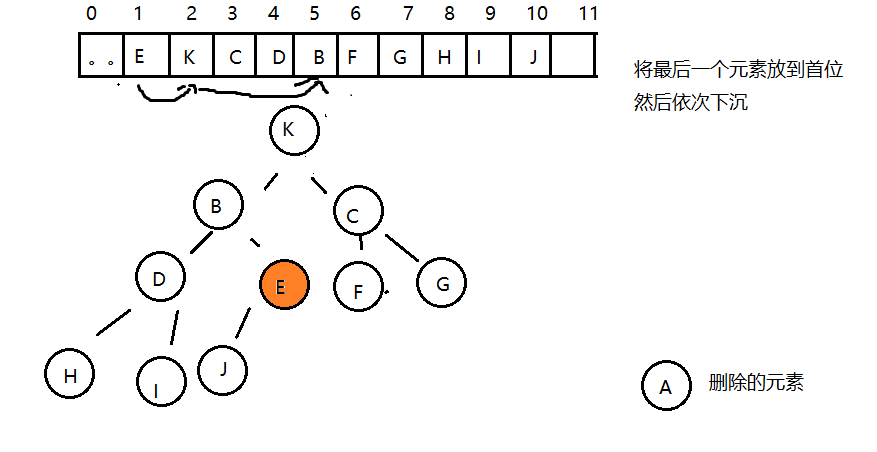
由堆的特性我們可以知道，索引1處的元素，也就是根結點就是最大的元素，當我們把根結點的元素刪除后，需要 有一個新的根結點出現，這時我們可以暫時把堆中最后一個元素放到索引1處，充當根結點，但是它有可能不滿足 堆的有序性需求，這個時候我們就需要通過一些方法，讓這個新的根結點放入到合適的位置。

所以，當刪除掉最大元素后，只需要將最后一個元素放到索引1處，并不斷的拿著當前結點a[k]與它的子結點a[2k] 和a[2k+1]中的較大者交換位置，即可完成堆的有序調整。

7.3.2.3 具體代碼

public class Heap {/*** 存儲元素*/private Integer[] items;/*** 記錄堆中的元素個數*/private int n;public Heap(int capacity) {items = new Integer[capacity + 1];n = 0;}/*** 判斷堆中索引i處的元素是否小于索引j處的元素** @param i* @param j* @return*/private boolean less(int i, int j) {return items[i] < items[j];}/*** 交換堆中索引i處和索引j處的值** @param i* @param j*/private void exch(int i, int j) {int temp = items[i];items[i] = items[j];items[j] = temp;}/*** 判斷堆中最大的元素，并返回這個最大元素** @return*/public Integer delMax() {// 獲取最大值Integer max = items[1];// 交換索引1 處和索引n處的值exch(1, n);// 刪除索引n處的值items[n] = null;// 個數-1n--;// 下沉sink(1);return max;}public int size() {return n;}/*** 往堆中插入一個元素** @param item*/public void insert(Integer item) {items[++n] = item;// 上浮swim(n);}/*** 使用上浮算法，使索引k處的元素能在堆中處于一個正確的位置** @param k*/private void swim(int k) {// 判斷k是否大于1，大于1的情況下再上浮while (k > 1) {// 比較當前節點和父節點，如果父節點比當前結點小，那么就交換if (less(k / 2, k)) {exch(k / 2, k);}k = k / 2;}}/*** 使用下沉算法，使索引k處的元素能在堆中處于一個正確的位置** @param k*/private void sink(int k) {// 判斷當前是不是數組末尾while (k * 2 <= n) {// 找到子節點中的較大者int maxIndex;if (k * 2 + 1 <= n) {// 存在右子結點if (less(k * 2, k * 2 + 1)) {// 左節點比右節點小maxIndex = k * 2 + 1;} else {maxIndex = k * 2;}} else {// 不存在右結點maxIndex = k * 2;}// 比較當前節點和子節點中的較大者，如果當前結點不小，就結束循環if (!less(k, maxIndex)) {break;}// 當前節點小，交換位置exch(k, maxIndex);k = maxIndex;}}public static void main(String[] args) {Heap heap = new Heap(11);heap.insert(5);heap.insert(1);heap.insert(2);heap.insert(8);heap.insert(7);heap.insert(9);heap.insert(11);heap.insert(4);heap.insert(6);heap.insert(10);heap.insert(3);while (heap.size() > 0) {int delValue = heap.delMax();System.out.println(delValue);}}}

7.3.3 堆排序☆

給定一個數組：

String[] arr = {“S”,“O”,“R”,“T”,“E”,“X”,“A”,“M”,“P”,“L”,“E”}

請對數組中的字符按從小到大排序。

實現步驟：

1. 構造堆；
2. 得到堆頂元素，這個值就是最大值；
3. 交換堆頂元素和數組中的最后一個元素，此時所有元素中的最大元素已經放到合適的位置；
4. 對堆進行調整，重新讓除了最后一個元素的剩余元素中的最大值放到堆頂；
5. 重復2~4這個步驟，直到堆中剩一個元素為止。

API設計

類名	HeapSort
成員方法	1.public static void sort(int[] source)：對source數組中的數據從小到大排序 2.private static void createHeap(int[] source, int[] heap):根據原數組source，構造出堆heap 3.private static boolean less(int[] heap, int i, int j)：判斷heap堆中索引i處的元素是否小于索引j處的元素 4.private static void exch(int[] heap, int i, int j):交換heap堆中i索引和j索引處的值 5.private static void sink(int[] heap, int target, int range):在heap堆中，對target處的元素做下沉，范圍是0~range。

構造堆，最直觀的就是直接把數組中的每一個元素都insert到堆中，這樣新的數組就是一個堆。這樣時間復雜度有點高了。

我們可以直接將原數組拷貝到items中，再從items中長度的一半位置處，從右往左掃描，對每一個元素進行下沉處理

代碼實現

    public static void main(String[] args) {Integer[] arr = {3, 6, 1, 2, 9, 7, 8, 4, 5, 10, 11};sort(arr);for (int i = 0; i < arr.length; i++) {System.out.println(arr[i]);}}public static void sort(Integer[] arr) {// 構造堆// 創建一個比原數組大1的堆Heap heap = new Heap(arr.length);heap.initHeap(arr);// 構造堆int index = heap.size();while (index != 1) {heap.exch(1, index);index--;// 交換完了，下沉heap.sink(1, index);}// 堆中的數據已經有序，拷貝到arr中for (int i = 0; i < arr.length; i++) {arr[i] = heap.get(i + 1);}}/*** 根據數組構造堆** @param arr*/public void initHeap(Integer[] arr) {// 遍歷數組，將數組中的元素添加到堆中for (int i = 0; i < arr.length; i++) {items[i + 1] = arr[i];n++;}// 從items的n/2位置遍歷到1位置for (int i = n / 2; i > 0 ; i--) {sink(i, n);}}/*** 使用下沉算法，使索引k處的元素能在堆中處于一個正確的位置** @param k*/public void sink(int k, int end) {// 判斷當前是不是數組末尾while (k * 2 <= end) {// 找到子節點中的較大者int maxIndex;if (k * 2 + 1 <= end) {// 存在右子結點if (less(k * 2, k * 2 + 1)) {// 左節點比右節點小maxIndex = k * 2 + 1;} else {maxIndex = k * 2;}} else {// 不存在右結點maxIndex = k * 2;}// 比較當前節點和子節點中的較大者，如果當前結點不小，就結束循環if (!less(k, maxIndex)) {break;}// 當前節點小，交換位置exch(k, maxIndex);k = maxIndex;}}

7.4 優先隊列

普通的隊列是一種先進先出的數據結構，元素在隊列尾追加，而從隊列頭刪除。在某些情況下，我們可能需要找出 隊列中的最大值或者最小值，例如使用一個隊列保存計算機的任務，一般情況下計算機的任務都是有優先級的，我 們需要在這些計算機的任務中找出優先級最高的任務先執行，執行完畢后就需要把這個任務從隊列中移除。普通的 隊列要完成這樣的功能，需要每次遍歷隊列中的所有元素，比較并找出最大值，效率不是很高，這個時候，我們就 可以使用一種特殊的隊列來完成這種需求，優先隊列。

優先隊列按照其作用不同，可以分為以下三種：

最大優先隊列：

可以獲取并刪除隊列中最大的值

最小優先隊列：

可以獲取并刪除隊列中最小的值

索引優先隊列：

可以根據索引去操作隊列中元素的值

7.4.1 最大優先隊列

最大優先隊列的實現就是堆的實現，前面已經講解過了，這里不再重復介紹。

7.4.2 最小優先隊列

最小優先隊列實現起來也比較簡單，我們同樣也可以基于堆來完成最小優先隊列。

我們前面學習堆的時候，堆中存放數據元素的數組要滿足都滿足如下特性：

1. 最大的元素放在數組的索引 1 處
2. 每個結點的數據總是大于或者等于它的兩個子結點數據。

其實我們之前實現的堆可以把它叫做最大堆，我們可以用相反的思想實現最小堆，讓堆中存放數據元素的數組滿足 如下特性：

1. 最小的元素放在數組的索引 1 處
2. 每個結點的數據總是小于或者等于它的兩個子結點數據。

這樣我們就能快速的訪問到堆中最小的數據。

API設計

類名	MinPriorityQueue
構造方法	MinPriorityQueue(int capacity)：創建容量為capacity的MinPriorityQueue對象
成員方法	1.private boolean less(int i,int j)：判斷堆中索引i處的元素是否小于索引j處的元素 2.private void exch(int i,int j):交換堆中i索引和j索引處的值 3.public T delMin():刪除隊列中最小的元素,并返回這個最小元素 4.public void insert(T t)：往隊列中插入一個元素 5.private void swim(int k):使用上浮算法，使索引k處的元素能在堆中處于一個正確的位置 6.private void sink(int k):使用下沉算法，使索引k處的元素能在堆中處于一個正確的位置 7.public int size():獲取隊列中元素的個數 8.public boolean isEmpty():判斷隊列是否為空
成員變量	1.private T[] imtes : 用來存儲元素的數組 2.private int N：記錄堆中元素的個數

代碼實現

public class MinPriorityQueue {/*** 存儲元素*/private Integer[] items;/*** 記錄堆中的元素個數*/private int n;public MinPriorityQueue(int capacity) {items = new Integer[capacity + 1];n = 0;}/*** 判斷堆中索引i處的元素是否小于索引j處的元素** @param i* @param j* @return*/private boolean less(int i, int j) {return items[i] < items[j];}/*** 交換堆中索引i處和索引j處的值** @param i* @param j*/private void exch(int i, int j) {int temp = items[i];items[i] = items[j];items[j] = temp;}public int size() {return n;}public boolean isEmpty() {return n == 0;}/*** 上浮算法，使索引k處的元素能在堆中處于一個正確的位置** @param k*/private void swim(int k) {// 如果沒有父結點，就不再上浮while (k > 1) {// 如果當前節點比父結點小，就交換if (less(k, k / 2)) {exch(k, k / 2);}k = k / 2;}}/*** 下沉算法** @param k*/private void sink(int k) {// 如果沒有子結點，就不需要下沉while (k * 2 <= n) {// 找出子結點中最小值的索引int minIndex = 2 * k;// 如果有右結點，并且右結點小于左節點if (k * 2 + 1 <= n && less(k * 2 + 1, k * 2)) {minIndex = 2 * k + 1;}// 如果當前節點小于子節點中的最小值，則結束循環if (less(k, minIndex)) {break;}// 當前節點大，交換exch(minIndex, k);;k = minIndex;}}/*** 插入方法** @param item*/public void insert(Integer item) {items[++n] = item;swim(n);}public Integer delMin() {// 取出最小值Integer min = items[1];// 交換最小值和最后一個值exch(1, n);// 刪掉最后一個元素items[n] = null;// 元素個數-1n--;// 下沉sink(1);return min;}}class Test12 {public static void main(String[] args) {MinPriorityQueue queue = new MinPriorityQueue(11);queue.insert(5);queue.insert(1);queue.insert(2);queue.insert(8);queue.insert(7);queue.insert(9);queue.insert(11);queue.insert(4);queue.insert(6);queue.insert(10);queue.insert(3);while (queue.size() > 0) {int delValue = queue.delMin();System.out.println(delValue);}}
}

7.4.3 索引優先隊列

在之前實現的最大優先隊列和最小優先隊列，他們可以分別快速訪問到隊列中最大元素和最小元素，但是他們有一 個缺點，就是沒有辦法通過索引訪問已存在于優先隊列中的對象，并更新它們。為了實現這個目的，在優先隊列的 基礎上，學習一種新的數據結構，索引優先隊列。接下來我們以最小索引優先隊列舉列。

實現思路

步驟一：

存儲數據時，給每一個數據元素關聯一個整數，例如insert(int k,T t),我們可以看做k是t關聯的整數，那么我們的實 現需要通過k這個值，快速獲取到隊列中t這個元素，此時有個k這個值需要具有唯一性。

最直觀的想法就是我們可以用一個T[] items數組來保存數據元素，在insert(int k,T t)完成插入時，可以把k看做是 items數組的索引，把t元素放到items數組的索引k處，這樣我們再根據k獲取元素t時就很方便了，直接就可以拿到 items[k]即可。

步驟二：

步驟一完成后的結果，雖然我們給每個元素關聯了一個整數，并且可以使用這個整數快速的獲取到該元素，但是， items數組中的元素順序是隨機的，并不是堆有序的，所以，為了完成這個需求，我們可以增加一個數組int[]pq,來 保存每個元素在items數組中的索引，pq數組需要堆有序，也就是說，pq[1]對應的數據元素items[pq[1]]要小于等 于pq[2]和pq[3]對應的數據元素items[pq[2]]和items[pq[3]]

步驟三：

通過步驟二的分析，我們可以發現，其實我們通過上浮和下沉做堆調整的時候，其實調整的是pq數組。如果需要 對items中的元素進行修改，比如讓items[0]=12,那么很顯然，我們需要對pq中的數據做堆調整，而且是調整 pq[5]中元素的位置。但現在就會遇到一個問題，我們修改的是items數組中0索引處的值，如何才能快速的知道需 要挑中pq[5]中元素的位置呢？

最直觀的想法就是遍歷pq數組，拿出每一個元素和0做比較，如果當前元素是0，那么調整該索引處的元素即可， 但是效率很低。

我們可以另外增加一個數組，int[] qp,用來存儲pq的逆序。例如： 在pq數組中：pq[2]=7; 那么在qp數組中，把7作為索引，2作為值，結果是：qp[7]=2;

當有了pq數組后，如果我們修改items[0]=12，那么就可以先通過索引0，在qp數組中找到qp的索引：qp[0]=5, 那么直接調整pq[5]即可。

API設計

類名	IndexMinPriorityQueue
構造方法	IndexMinPriorityQueue(int capacity)：創建容量為capacity的IndexMinPriorityQueue對象
成員方法	1.private boolean less(int i,int j)：判斷堆中索引i處的元素是否小于索引j處的元素 2.private void exch(int i,int j):交換堆中i索引和j索引處的值 3.public int delMin():刪除隊列中最小的元素,并返回該元素關聯的索引 4.public void insert(int i,T t)：往隊列中插入一個元素,并關聯索引i 5.private void swim(int k):使用上浮算法，使索引k處的元素能在堆中處于一個正確的位置 6.private void sink(int k):使用下沉算法，使索引k處的元素能在堆中處于一個正確的位置 7.public int size():獲取隊列中元素的個數 8.public boolean isEmpty():判斷隊列是否為空 9.public boolean contains(int k):判斷k對應的元素是否存在 10.public void changeItem(int i, T t):把與索引i關聯的元素修改為為t 11.public int minIndex():最小元素關聯的索引 12.public void delete(int i):刪除索引i關聯的元素
成員變量	1.private T[] imtes : 用來存儲元素的數組 2.private int[] pq:保存每個元素在items數組中的索引，pq數組需要堆有序 3.private int [] qp:保存qp的逆序，pq的值作為索引，pq的索引作為值 4.private int N：記錄堆中元素的個數

*************************************優雅的分割線 **********************************

分享一波:程序員賺外快-必看的巔峰干貨

如果以上內容對你覺得有用,并想獲取更多的賺錢方式和免費的技術教程

請關注微信公眾號:HB荷包

一個能讓你學習技術和賺錢方法的公眾號,持續更新