在上一篇文章中,我們介紹了一種最簡單的MDP——s與a都是有限的MDP的求解方法。其中,我們用到了動態規劃的思想,并且推出了“策略迭代”、“值迭代”這樣的方法。今天,我們要來講更加一般的最優控制問題——t、a與s都是連續的問題。我們仍然假定我們已經清清楚楚知道環境與目標。我們將介紹求解的方法,并引出Hamilton-Jacobi-Bellman方程(簡稱H-J-B方程)。其中,H-J-B方程是一個t連續定義下的方程,它的離散t的版本被稱作Bellman方程。這在強化學習中是極其重要的。
最優控制問題
在最優控制中,我們一般用x來代表狀態,用u來代表“控制”,即可以人為輸入的東西,和MDP中的動作a是同一個概念。另外,在最優控制中,我們一般不是嘗試“極大化獎勵”,而是嘗試“極小化損失”,也就是說,我們的目標往往是用一個求極小化的形式表現出來(只要加上一個負號就可以實現二者的轉化)。除此之外,最優控制與MDP最大的不同在于其t是連續的。在進行了概念的對應之后,最優控制的邏輯和MDP都是一樣的。
按理說,s與a是連續的時候,也可以將動作、狀態的轉移建立為一個概率方程。例如給出在
一般的最優控制問題有如下幾部分組成(用x記狀態、用u記控制/動作)。首先是給定初始與終止的時間
如果問題是time-invariant的,則可以去掉t變量,即變成
問題的目標是極小化損失函數:
同理,對于time-invariant的問題,f中的t變量可以省略。作為目標的損失函數分成兩個部分,一個是在路徑上累積損失,用f記錄,另一個是最終狀態對應的損失,用H記錄。路徑上的累積損失意思是在時間微元
很多問題可以轉化為最優控制問題。例如對于一個在平地上開汽車的問題,限定一定時間內(截止為

有了最優控制問題之后,我們當然可以開始對其進行求解。這里的t、a與s都是連續的,而對于狀態轉移方程函數
作為最優控制的例子,我們可以先考慮一種最簡單的、可以求出解析解的最優控制問題。那么,怎么才算是“最簡單”呢?
首先,我們希望Dynamic
然后考慮損失函數
這種Dynamic是線性(Linear),而損失函數是二次函數(Quadratic)的情況是最簡單的一類最優控制問題,我們將其稱作LQR(Linear-Quadratic Regulator)。一個time-invariant的,并且沒有狀態與控制的交錯項的LQR,就是我們所找尋的“最簡單的”問題:

上述的LQR是最優控制中最簡單,同時也是最經典的一類問題,常常被作為最優控制教材的“入門問題”出現。對于這類問題,我們可以不對x與u進行離散化,而直接精確地求出其最優解的表達式。
針對不同的最優控制問題,或簡單,或復雜,我們同樣利用動態規劃的思想,可以有幾種不同的解法。其中最主要的問題是,我們是否要對連續的t進行離散化。如果對t進行離散化之后,對于簡單的LQR問題,我們有比較簡單的方法求出解析解(不用對x與u離散化)。而對于非線性的系統,我們則只能對x與u進一步離散化,求近似的數值解;如果我們選擇不對t進行離散化,則可以將問題轉化為一個偏微分方程,也就是我們今天的主題Bellman方程。(有許多非線性pde求不出解析解,同樣只能求數值解,但這又是另一個問題了)。這幾種情況中,核心的思想都是動態規劃。
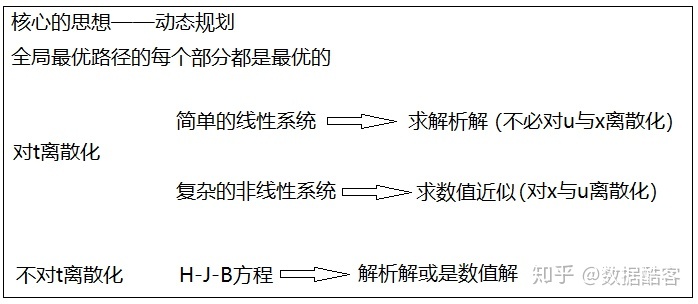
下面,我們就來一一介紹這些方法。
離散化t求數值解
面對t連續的問題,尤其是非線性的、復雜的問題,我們無法求出精確的解析解。所以,將t離散化不失為一種明智之舉。
將t離散化之后,關于t的連續函數

我們首先來講LQR問題的求解方法。這個過程中要利用到我們上一章動態規劃的思想,以及對于“價值”的定義。我們不妨設t是從0到100的:
首先,我們已知在最終狀態下,狀態
然后,我們考慮t=99的時候,已知狀態
接著,我們考慮t=98的時候,
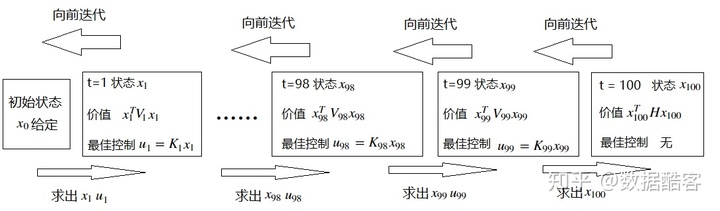
接下來,我們可以不斷地重復這個過程。由于LQR的定義——Dynamic是線性,而懲罰函數是二次的這個性質,最佳控制
我們一直重復這個迭代過程,直到初始狀態
對于非線性的問題,我們也想要仿照上述的方法。但是,如果將過程中每一步的最佳控制與價值表達為狀態的解析表達式,可能會得到極其復雜的表達式。例如,如果將LQR中的Dynamic從線性的形式改為二次的形式,則我們會發現迭代了幾步之后就無法再迭代下去了。對于這樣的情況,我們無法求解析解,只能考慮通過離散化x與u來求數值解。
例如,我們將x、u離散化為10段得到一個狀態有共10種,控制有
首先,考慮所有最終狀態對應的價值:
然后,計算t=99的時候從所有狀態出發時能夠獲得的價值。我們應該遍歷能夠采取的控制u,來計算每個狀態的價值。例如對于狀態$x_1$,采取$u_1$控制會讓其進入$x_8$的狀態,那么它就能在t=99到t=100的瞬間內獲得$f(x_1,u_1,t)$的“累積損失”,并且獲得$H(x_8)$的“最終狀態損失”。我們對狀態$x_1$計算每一個$u_i$帶來的“累積損失”與“最終損失”之和,挑出其中最小的(注意最優控制問題的目的是要讓損失最小)。我們可以得到一個這樣的結論:在t=99的時候,對于狀態$x_1$,采取$u_3$是最好的,它可以讓后面發生的損失低至48.4。此時,我們就將48.4記作$x_1$的“價值”。
接著,計算t=98時候所有狀態x的價值,以及其對應的最佳控制u。這個過程要用到上一個步驟的數據,例如t=98時,在$x_1$采取$u_1$,除了會立即獲得一個“累積損失”之外,還會在t=99的時候就會進入$x_6$。而t=99的時候$x_6$到底好不好,我們就要參考上一個步驟計算出的各個$x_i$在t=99時候的價值。這個步驟結束后,我們可以得到形如這樣的結論:t=98時,對于狀態$x_1$,采取$u_2$是最好的。它可以讓后面發生的損失低至84.8。然后,我們就將84.8記作$x_1$的“價值”。
接下來,不斷向前迭代上述步驟。要注意的是,迭代的每個步驟中必須將所有的中間結果保留下來。例如在t=84的時候$x_1$的價值很大,也就是說t=84時候進入$x_1$后面會面臨很大的損失,所以不是一個好的選擇。但是你不能因此就將這條數據丟掉,因為說不定你的前半程可以只用很小的損失來到這個狀態。我們不斷向前迭代算法直到t=1的時刻。當我們算出t=1的時刻,各個狀態x對應的最優控制u與價值的時候,我們就可以考慮在t=0的初始狀態
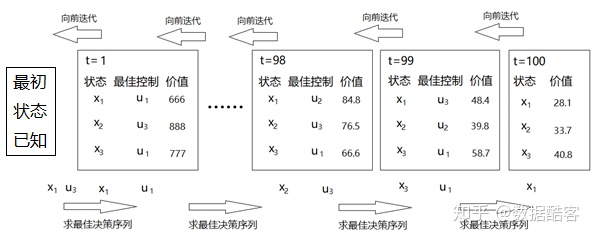
對于原本的問題,由于有100個回合,每個回合都有10種控制,所以有
細心的讀者可能發現了,我們上面講到的兩種迭代本質上是一樣的,都是要向前求出“最佳控制”與“價值”關于當前狀態的表達式。在LQR中,由于表達式是線性的,或者是二次的,所以我們可以真真切切地把解析表達式求出來。而在復雜的非線性問題中,由于我們求不出解析式,所以我們只能用離散化的方法,用一張表格的形式記錄狀態與“最佳控制”以及“價值之間”的對應關系。可以想象,如果將表格記錄的內容可視化,我們會看到一個高度非線性、無法求出表達式的函數圖像。

上面所說的方法和我們上一章講的“井字過三關”的思路其實是一樣的,都是對狀態建立“價值”,然后向前迭代求解。并且,因為我們的模型是確定性的,所以每次計算價值的時候不用計算期望,所以計算過程事實上還要簡單很多(在“井字過三關”中,我們由于利用了畫圖求解的直覺,以及對稱性,所以省略了很多步驟。如果將其嚴謹寫出來會很繁瑣)。
對于LQR問題來說,我們采用解析式迭代的方法可以求出比較精確的解。但是對于非線性的問題來說,離散化的時候我們會面臨計算復雜度與精度的權衡取舍。因為在離散化的時候,我們可以人為地選擇將x分成10個不同的狀態,也可以分成100個不同的段。如果我們選擇將x與u均分為更多的段,這意味著結果的精度更高,但同時也意味著計算的時間復雜度會更多;如果將x與u只分成較少的段,計算的時間復雜度會降低,但是計算的精度卻會下降。并且由于算法是迭代的,這種誤差傳遞到后面可能會變得很大。如何權衡取舍這兩者得到綜合最佳?這并不是一個簡單的問題,需要視具體情況而定。
H-J-B方程
在上面一節中,我們首先對t進行了離散化,然后再針對問題簡單與復雜的情況,分別介紹了求解析解以及離散化求數值的方法,它們都是通過迭代而實現的。那么,我們現在的問題是,能不能不要對t進行離散化,而是把t作為連續變量來直接求解析解呢?答案是肯定,并且,這正是我們本節主題——H-J-B方程的內容。
事實上,推出H-J-B方程可以說和我們上一節思路是完全一樣的,只不過是將時間的差分
定義一個價值函數
在最佳$u(t)$作用下,我們能夠獲得的總價值為
根據
對
將上面兩個式子相減,再除以$dt$,并且讓$dt$趨于0,得到以下方程:
這個過程可以類比于上一節中我們從后向前迭代推出V表達式的過程。本質上,V是一個關于x與t的二元函數。上一節中,我們迭代中將V拆分成了
將環境
這個方程就是大名鼎鼎的H-J-B方程。我們將
將
這里貼一個公開課上H-J-B方程的截圖。要注意其使用的符號可能與我們有所出入:

下面,我們來看一個求解H-J-B方程的簡單的例子:
環境方程為
懲罰函數為
首先,我們有哈密頓量
它關于u的導數為:
解出H關于u的一個駐點為
然后,我們發現
這也就意味著,
我們將
方程:
邊界條件:
這就是一個典型的關于二元函數
這便是我們所求的最優控制問題的解析解。
細心的讀者可能想到,我們舉的這個例子其實也是一個“最簡單”的LQR問題。如果這不是一個LQR問題,而是一個更加復雜的非線性問題,我們還能這樣求解嗎?實話實說,我們只能保證可以按照H-J-B方程的定義將pde列出來,但是卻不能保證求出解析解,因為有許多pde是沒有辦法求解析解。對于這樣的pde,唯一的方法仍是求數值解。而一旦我們考慮求數值解,那又要離散化t。這也意味著,求H-J-B方程數值解的過程,事實上和上一節講的離散化t求迭代算法是完全等價的。所以說,離散與連續之間可以相互轉化——離散問題的極限情況有助于我們理解連續的方程是怎么推導出來的,而連續方程有時候又要借助離散化來求近似的數值解。
總的來說,只有在問題比較簡單,例如LQR問題的情況下,我們可以離散化t以求迭代的解析式,也可以不離散化t,直接求解H-J-B方程的解析解;而在問題比較復雜的問題中,我們只能求數值解。哪怕是列出了H-J-B方程,還是只能求方程的數值解。
這兩期的總結
最優控制中有兩大類算法,一類是動態規劃與H-J-B方程,另一類是變分法與龐特里亞金原理。在上一章與本章中,我們著重講了動態規劃與H-J-B方程。它有一個基本的思想,即把全局最優的解的每一個部分單獨挑出來也是最優解。根據這個原理,就可以將一個整體的問題給拆分成局部的小問題,依次求解,大大地節省計算量(從指數復雜度降低到線性復雜度)。用來連接“大問題”與“小問題”的量就是“價值”V。我們講到的所有算法都圍繞著“價值”的計算和極大化而展開。
在這兩章中,我們講的問題給人一種感覺——只有比較簡單的幾類的最優控制問題可以解決。第一類是s與a(或者x與u)都是離散的,它們之間具有確定性的轉移關系的。我們可以用本文中第二節的迭代方法解決;第二類是s與a都是離散的,它們之間具有隨機轉移關系的。這類方法和第一類差別并不大,只要加一個期望就行了。由于我們討論的是完全已知模型的情形,所以期望公式可以直接得到;第三類是s與a是連續的,但是其中的轉移關系是比較簡單的,比如LQR。其他的問題,例如s與a是連續的,并且轉移關系很復雜的情況,是沒有辦法求解的,只能通過離散化使之成為第一類來求近似的數值解。
在強化學習中,有兩種解決問題的思路,一種是基于價值的方法,另一種是基于policy的方法。其中,基于價值的方法正是從最優控制問題中動態規劃方法發展而來,它同樣也是通過擬合“價值”來求解最佳策略。不過,強化學習還將動態規劃的思路結合了深度學習的方法。在最優控制中,我們認為只有s與a之間關系是簡單的線性關系時才能求解析式,而當它們關系是復雜的非線性關系時,就只能先離散化s與a,再用一個表格的形式去記錄s與a的對應關系。但是,當我們有了神經網絡這個工具后,我們就可以嘗試去擬合任意復雜的非線性函數,無論是s與a之間或是s與V之間的關系。這也使得我們不必拘泥于上面三種簡單的情況,而可以考慮更加復雜的情況。
另一方面,強化學習也有十分困難的地方。例如在這兩章中,我們都假定完全已知模型。這才導致s與a之間的轉移關系具有隨機性的時候不會顯著增加問題的難度——因為我們已知轉移概率,可以直接列出期望的表達式。但是,當我們未知模型的時候,如何能夠準確地近似出V?如何減小估算的偏差與方差?如何避免局部收斂?這就涉及到探索-利用(explore-exploit),同策略-異策略(on-policy)之間的取舍,大大地增加了問題的復雜度。這些我們接下來都會慢慢講到。















 從傅里葉級數到傅里葉變換...)


:Mybatis初始化1.3 —— 解析sql片段和sql節點)
