在上一部分當中，得到了利用三角函數表示周期函數的方法，但是對于非周期函數就...涼了。所以有什么辦法嗎？沒辦法（劃掉）。這時候我們就需要拿出來我們的黑科技——傅里葉變換。

一、傅里葉級數的推廣

當然這東西肯定不是憑空腦補出來的，而是將傅里葉級數進一步推廣到非周期函數上。現在已經得到了周期函數的情況，一種很自然的想法就是將非周期函數化歸到周期函數上，那么就可以繼續套用傅里葉級數了。

如果要強行描述非周期函數的周期性，那它的周期就應該是無窮大，整個定義域都在它的一個周期內，以至于它不可能再重復這一周期。

把這個想法用形式化的語言表示出來，就是

的周期

。因為

，那么

。接下來觀察一下此時的傅里葉級數

。不大容易觀(xuan)察(xue)，三角形式有點復雜，不如采用指數形式

。

當

時，

從原本的離散變化變成了連續變化，

也就可以表示為關于

的函數

。

傅里葉級數中

，事實上，這個積分的上下限不一定是

到

，只需要積

的一個周期就可以了。

換句話說，對于任意的

，系數可以表示為

。

這個積分需要積一整個周期，而此時的周期為無窮大，也就是整個定義域上都需要積，所以要從

積到

。

只需要讓上式中的

，

，便可以得到

的表達式。不妨令

，就得到了

。

因為

，所以

？當然不是，右側的積分可能為無窮大，無窮小與無窮大的積不一定為無窮小。（如果等于零的話豈不是很有毒）

但是這對無窮大和無窮小的階并不好比較，我們得不出

究竟應該等于什么值。既然

這么煩，那不如把它從這里面丟出去，之后用到

的時候再乘回來就好了，

。

現在有了傅里葉級數對應的系數，該搞一搞

這個式子了。把對應的系數

代進去，再代入

，變形后有

因為

，每次

的增量

都是由于

變為

造成的，所以

。

同時

連續變化，原本的離散意義下的求和就該變為連續意義下的積分，搞出來

。

至此便推導出了傅里葉變換的兩個公式

上式稱為傅里葉變換，下式稱為傅里葉逆變換。

還有另一個版本的傅里葉變換是

這兩個版本都差不多，不過就是

這個系數的處理方法不大一樣。mathematica上采用的是第二個版本的傅里葉變換，之前算了半天都跟自己手算的不一樣，還以為自己算錯了（溜

二、傅里葉變換的條件

由于傅里葉變換是從傅里葉級數推導得來的，所以還是狄利克雷條件，不過此時還要加上第三條，

在一個周期內絕對可積。

這一個條件在

為周期函數時，可以由前兩個條件推出來，因為周期和函數值均為有限值，所以在一個周期內一定絕對可積。但是推廣到傅里葉變換后，這個推導就不成立了，需要單獨判定第三個條件。

三、性質

以下均默認

表示可以進行傅里葉變換的函數，

，

函數的卷積

1、線性性質：

,

2、尺度變化：

，

3、對稱性：

4、時移性：

，

5、頻移性：

，

6、時域卷積定理：

7、頻域卷積定理：

8、微分運算：

這些運算性質都是在采取第一種形式的傅里葉變換下的性質，如果使用第二種形式，會在某些性質上帶來常數因子上的差別。

前面的7種運算性質的證明用積分的性質，再做點變量代換亂搞搞就可以了。這里主要說下微分運算性質的證明，用分部積分。只用證一階導的情況就可以了，證出來之后使用數學歸納法可以很容易地推廣到任意階導數的情況。

微分運算的性質使得傅里葉變換能夠將復雜的微分運算轉化為簡單的乘法運算，所以這個性質的常見應用在于解微分方程。通過傅里葉變換使微分方程變為代數方程，解出代數方程后再利用傅里葉逆變換求出原微分方程的解。

舉個栗子，解物理上的簡諧振動方程，除了常用的特征根法，還能夠使用傅里葉變換

令

，方程兩邊同時傅里葉變換

定義

，

使得

。

解出

，

為常數

進行逆變換

使用輔助角公式合并

，

,

為常數

傅里葉變換在微分方程上的應用不局限于此，還能夠應用于偏微分方程。但是最常用的并不是傅里葉變換，而是它的一般形式拉普拉斯變換

四、廣義傅里葉變換

在實際問題當中，經常會遇到一些函數并不滿足絕對可積的條件，因而它們對應的傅里葉變換積分發散，并不存在傅里葉變換。但是我們又需要它們的傅里葉變換，所以就有了廣義上的傅里葉變換。

比如剛剛求的簡諧振動方程，對應的代數方程解出來后，發現

是發散的，此時我們通過定義了一個新函數

解決了發散的問題。暫時無視掉函數發散的問題，帶著無窮大繼續運算，最后逆變換時再作處理，這便是廣義傅里葉變換的核心思想。

考慮正余弦函數，它們嚴格意義上的傅里葉變換都是不存在的，但是可以表示為

五、幾何意義

傅里葉變換的幾何意義類似傅里葉級數，當

時，所有的三角函數

，

，

，

(

)兩兩正交。換句話說，所有的三角函數都作為基向量，將

向它們投影。

實際上，無論是傅里葉級數還是傅里葉變換，都是在無窮維的希爾伯特空間中，將函數定義為空間中的向量，通過三角函數這樣一組基向量表示空間中的任意函數。

六、物理意義

emm這一部分跟數學和oi的關系都不是特別大，就大概簡略的寫一下了，詳細的介紹在網上也有很多資料，詳細寫的話怕是能再寫這么長一篇文章（我懶）。

傅里葉級數將函數分解到離散的頻率之上，而傅里葉變換將函數分解到連續的頻域中，這樣使原本頻域上離散的點變成一條連續的曲線，對應的就是

的圖像。

描述的是

在

這個頻率分量上的大小。

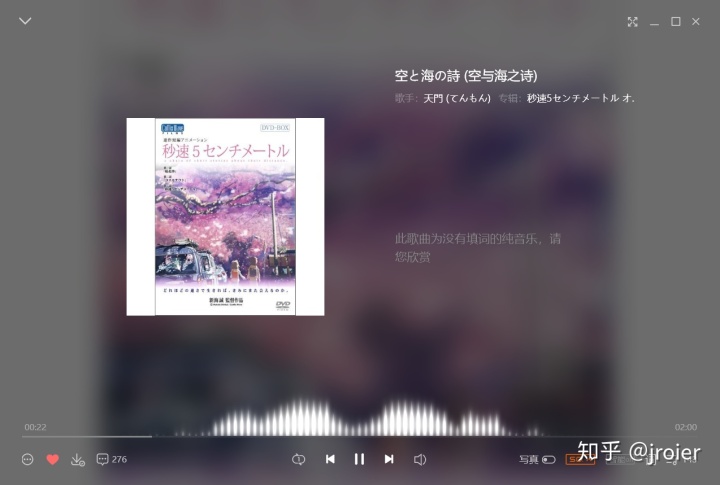
基于這樣的物理意義，傅里葉變換在實際問題當中得到大量應用。比如說最常見的是音樂軟件上那個瘋狂抖動的條，我也不知道這東西叫啥，反正就是下面這個圖里進度條上面的那一坨。這個東西實際上是把現在正在播放的音頻進行傅里葉變換，畫出的頻域圖。

還有一種應用是視頻以及圖片的防偽和防盜版鑒別當中。將畫面進行二維傅里葉變換，疊加高頻分量，再進行逆變換即可。高頻分量帶來的差異很小，肉眼難以分辨，而且難以通過簡單的截圖和p圖操作消除高頻分量，因而是一種十分有效的“水印”。

除此以外，音視頻的壓縮也可以采用傅里葉變換，只保留強度較高的頻率，去除較弱的頻率，減少存儲的數據量。