559. N 叉樹的最大深度

給定一個 N 叉樹，找到其最大深度。

最大深度是指從根節點到最遠葉子節點的最長路徑上的節點總數。

N 叉樹輸入按層序遍歷序列化表示，每組子節點由空值分隔（請參見示例）。

示例 1：

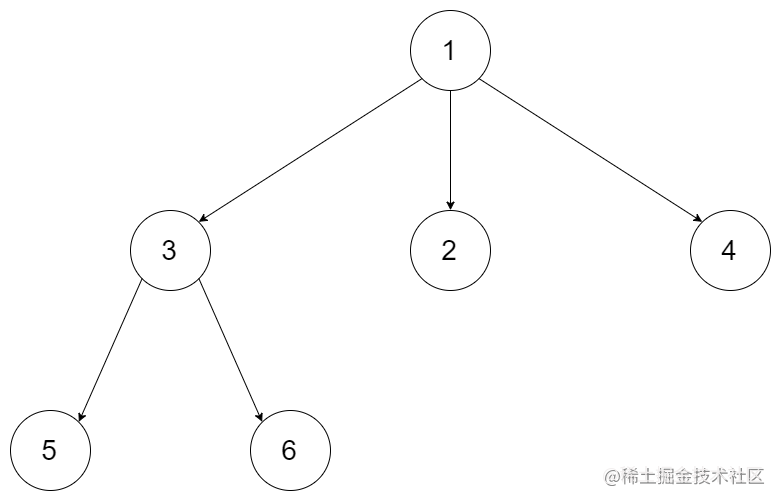
輸入：root = [1,null,3,2,4,null,5,6]

輸出：3

• 示例 2：

輸入：root =
[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]

輸出：5

提示：

• 樹的深度不會超過?1000 。
• 樹的節點數目位于 [0,?104] 之間。

解題思路

使用遞歸，每個遞歸函數返回的是以輸入參數root為根節點的子樹，所具有的最大深度。每次遞歸計算所有的子節點，得出子節點中的最大深度，然后加上當前節點的深度一，返回給上層調用。

代碼

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:int maxDepth(Node* root) {if (root== nullptr) return 0;int res(0);for (auto c:root->children)res=max(maxDepth(c),res);return res+1;}
};

時間復雜度：$O(n)$，其中 n 為 N 叉樹節點的個數。每個節點在遞歸中只被遍歷一次。

空間復雜度：$O(\text{height})$，其中$ \textit{height}$ 表示 N 叉樹的高度。遞歸函數需要棧空間，而棧空間取決于遞歸的深度，因此空間復雜度等價于 N 叉樹的高度。

解題思路

利用隊列實現對N叉樹的層序遍歷，并且記錄下訪問到的最大的層數，就是最大深度

代碼

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:int maxDepth(Node *root) {if (root == nullptr) return 0;int res(0);queue<Node *> q;q.push(root);while (!q.empty()) {int s = q.size();for (int i = 0; i < s; ++i) {Node *cur = q.front();q.pop();for (auto c:cur->children) {if (c != nullptr)q.push(c);}}res++;}return res;}
};